1.2.8. Построение тднф недоопределенных бф.
Есть много методов удаления из ДНФ избыточных конъюнкций. Наиболее просты табличные, наиболее точны - аналитические.
К числу простейших способов преобразований относится последовательное использование законов поглощения и обобщенного склеивания.
Рассмотрим пример.
Можно при поиске ТДНФ (или близких к ним ДНФ) использовать таблицы покрытий, размечая столбцы конъюнкциями из исходной D1, а строки совокупностью простых импликант, построенных по D1.
На практике столбцы удобно размечать кодами конъюнкций из исходной D1, ставя метку в клетке (i,j), если Ki = 1 после подстановки в нее константных значений из кода конъюнкции j-ого столбца.
Процедура поиска ТДНФ по таблице покрытий рассматривалась ранее (если исходная ДНФ D1 была представлена ДСНФ, то ее коды фактически совпадают с наборами из М1 и наша таблица в точности совпадает с таблицами покрытий, рассматривавшимися ранее).
Рассмотрим пример.
D1исх
=
D1
=
-
0-00
0001
0101
1101
1001
0-11
*
*
*
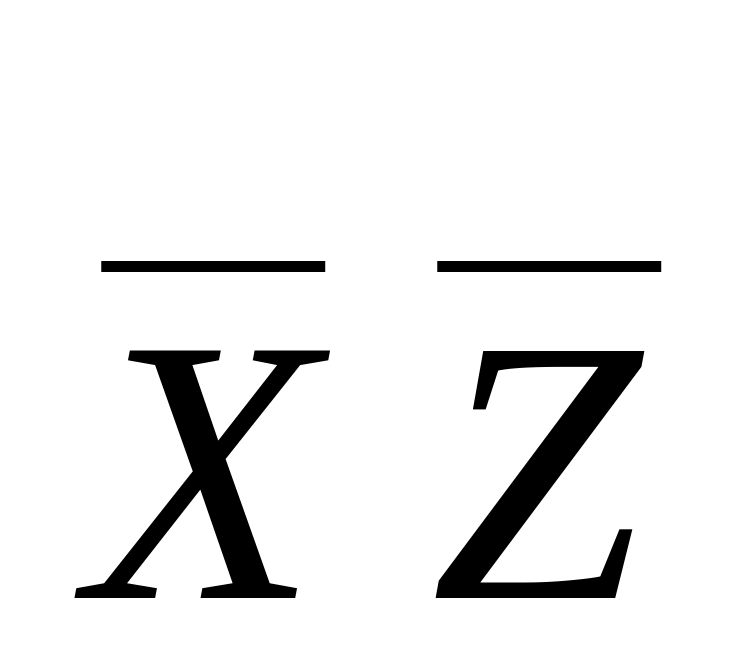
«ядро»
*
*
*
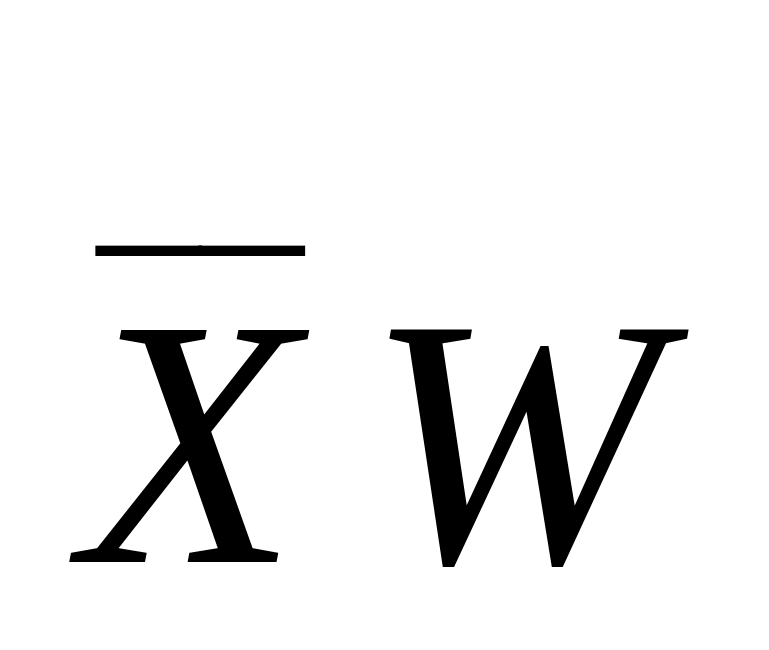
«ядро»
*
*
*
*
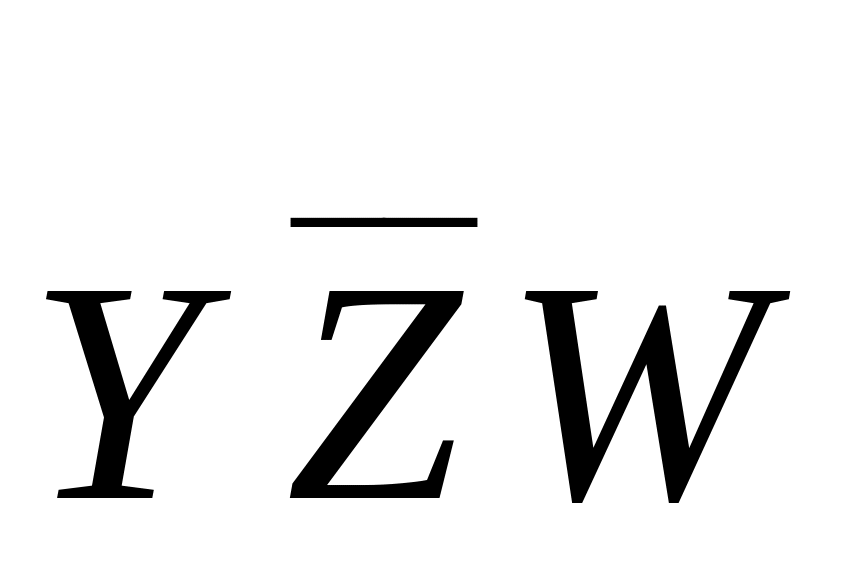
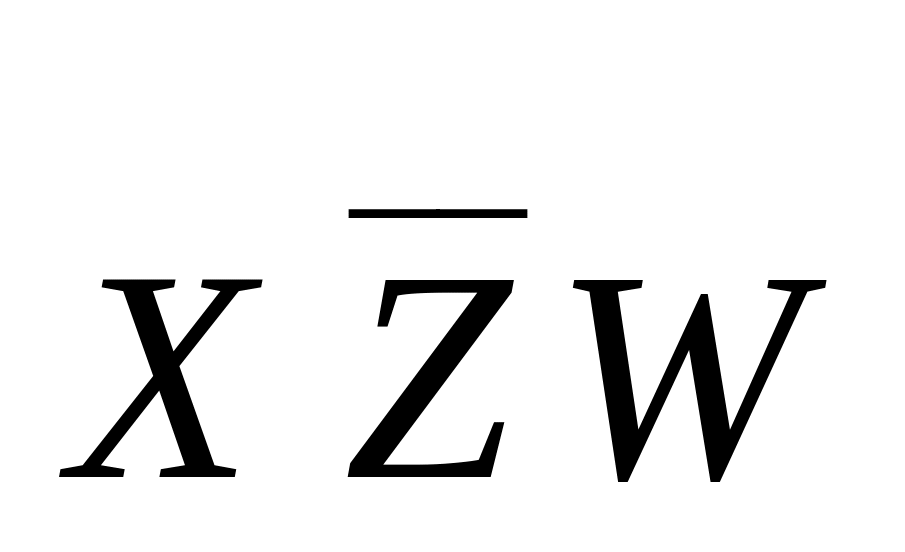
«ядро»
F
=
Наиболее хорошие результаты можно получить, если столбцы размечать отдельными наборами из М1, но их не всегда можно построить по исходной ДНФ D1 из-за того, в М1 их может быть слишком много.
1.2.9. Карты Карно.
Рассмотрим принципы визуальных методов минимизации БФ (карты Карно, диаграммы Вейча, графы и др.).
Множество всех наборов значений переменных представляется специальной фигурой.
Конъюнкция представляется наглядным графическим образом, легко обнаруживаемым на используемой специальной фигуре (правильная конфигурация.)
Поиск ДНФ - визуальный поиск покрытия области М1 по правильными конфигурациями.
Поиск покрытия в основном за интуицией человека!
Рассмотрим функцию от двух переменных (n =2).
Фигура, представляющая множество всех наборов значений переменных - плоскость.
Н а плоскости - прямоугольная таблица, каждая клетка которой представляет набор значений переменных.
X Y |
0 |
1 |
Клетки размечаются значениями функции
|
X |
Y |
F |
0 |
1 |
0 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
1 |
1 |
|
|
|
|
1 |
0 |
0 |
|
|
|
|
1 |
1 |
1 |
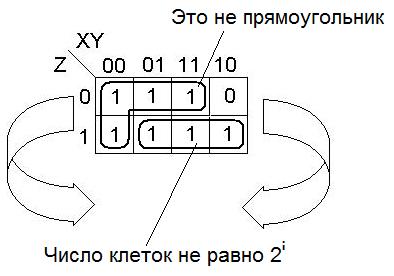
В таблице выделяется прямоугольник из соседних клеток, число которых равно целой степени двух (правильная конфигурация) и функция в них принимает значение «1».
Код конъюнкции – набор значений переменных, описывающих клетки правильной конфигурации. Переменная, чье значение сохраняется неизменным во всех клетках конфигурации отображается в коде эти значением, остальные переменные - прочерком «-».
Конъюнкция получается по ее коду.
Рассмотрим пример.
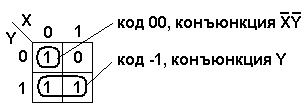
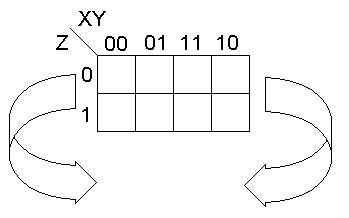
Рассмотрим карту Карно для функции от трех переменных (n =3).
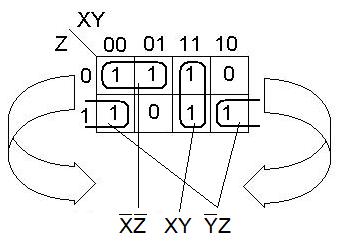
Фигура, представляющая множество всех наборов значений переменных - развертка цилиндра (есть соседства через левый и правый край).
Примеры правильных конфигураций.
|
|
|
|
Примеры «неправильной» конфигурации.
Рассмотрим карту Карно для функции от четырех переменных (n =4).
Фигура для всех наборов значений переменных - развертка тора (есть соседства через все края).
|
|
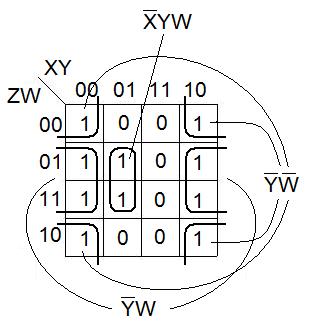
Поиск ДНФ сводится к поиску покрытий М1 по правильным конфигурациям.
Рассмотрим примеры.
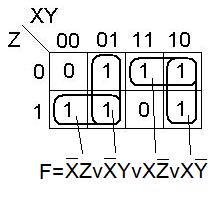
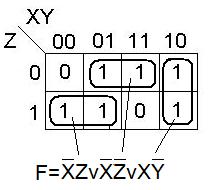
Данную функцию можно представить в более коротком виде.
Пример нахождения ДНФ для функции от 4-х переменных.
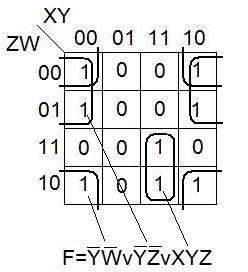
При построении ДНФ по карте Карно, критерием является ранг покрытия - число букв задаваемой им ДНФ. Наш задача – получить минимум.
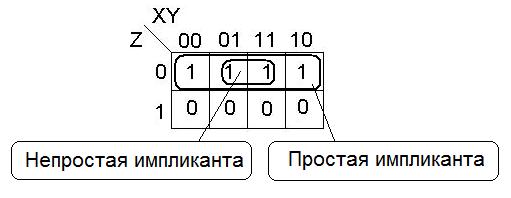
Простая импликанта имеет образ правильной конфигурации, не являющейся частью одной другой.
Пример простой импликанты.
Для
недоопределенной БФ F~
строится покрытие, у
которого М1
М~
М
М1
Все «единицы» должны быть покрыты и, при этом, могут быть покрыты клетки с «~», то есть клетки области неопределенности. Это позволяет уменьшить количество букв в ДНФ.
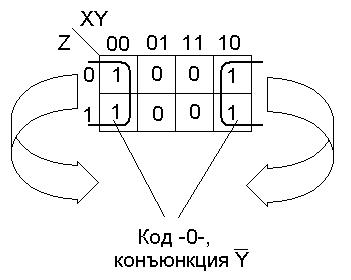
Рассмотрим пример.
Примечание.
Для нахождения МДНФ - области покрытия должны быть максимально возможными, а количество областей и их пересечение необходимо свести к минимуму.
Для нахождения СДНФ - области должны быть максимально возможными, должны быть представлены все возможные области (максимальное количество пересечений областей).
Рассмотрим пример нахождения СДНФ по карте Карно.
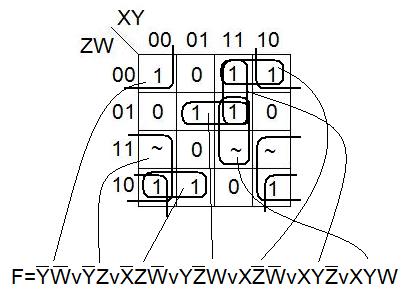
Рассмотрим пример нахождения МДНФ по карте Карно.
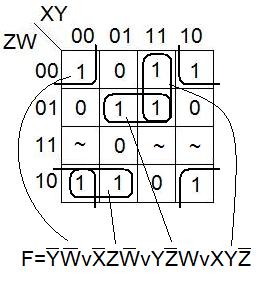
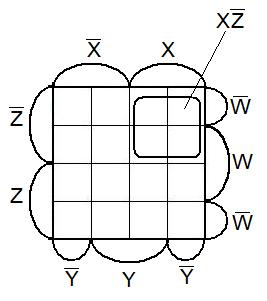
Карты (диаграммы) Вейча строятся аналогично картам Карно.
Правильная конфигурация здесь описывается конъюнкцией. По конъюнкции можно получить ее код, а затем по коду можно получить ее М1.
(В картах Карно наоборот - по наборам получается код конъюнкции, а по коду сама конъюнкция.)
