1.2.2. Пути решения задачи упрощения днф бф.

Основная проблема при работе с БФ – это проблема минимизации.

Существует различные способы минимизации. Рассмотрим основные принципы некоторых из них.

Первый способ. В данном случае исходной является ДСНФ. По ней строится СДНФ, а из СДНФ получают несколько ТДНФ, и из них производится выбор МДНФ или кратчайшей ДНФ.

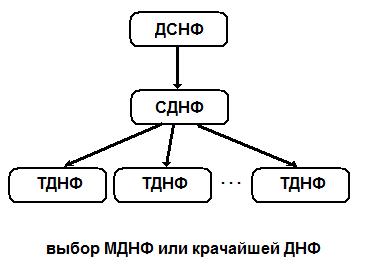
Для «почти всех БФ» переход от ДСНФ к СДНФ сопровождается усложнением, так как длина СДНФ составляет, по крайней мере, , где .

При этом конъюнкции СДНФ имеют не менее (n-logn-1), букв.

Несмотря на это СДНФ при поиске МДНФ необходимо получать, так как в общем случае не имея всех простых импликант, нельзя найти МДНФ.

Число ТДНФ для «почти всех БФ» очень велико.

При этом минимальных или кратчайших ДНФ очень мало. Перебрав небольшое число ТДНФ нельзя статистически достоверно получить МДНФ.

Но, встречающиеся на практике БФ таковы, что СДНФ у них, не слишком сложны, а расхождения в числе букв у МДНФ и наиболее сложной ТДНФ не слишком велики.

В связи с этим на практике используются и другие методы упрощения ДНФ.

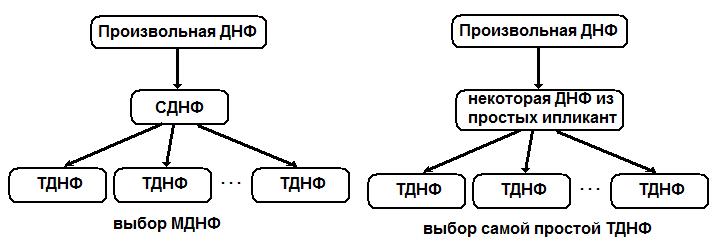
Нахождение ТДНФ для задач большой размерности может быть выполнено следующим образом: для произвольной ДНФ производится получение простых импликант, а затем удаление избыточных конъюнкций. Таким образом, получается произвольная ТДНФ.

1.2.3. Построение сднф по дснф.

СДНФ строят, используя разные подходы, но при этом, можно выделить два основных:

1. Генерация всех возможных конъюнкций исходных переменных и проверка их на наличие свойств простой импликанты рассматриваемой БФ;

2. Формирование всех простых импликант БФ по конъюнкциям из исходной ДСНФ (либо некоторой ДНФ) БФ.

Первый подход порождает много разных методов, отличающихся по организации перебора вариантов при генерации кодов конъюнкций. Эти методы наиболее удобны и эффективны при «машинном» решении задач.

Проверки конъюнкций чаще всего выполняют по М₀.

Рассмотрим пример.

Пусть F(X,Y,Z) имеет М₁=(001, 010,011,100,101,110) и, соответственно, М₀=(000,111).

Необходимо определить является ли конъюнкция простой импликантой БФ F.

Для переменных (X,Y,Z) М₁( )=(000, 001).

Так как 000 - набор из М₀(F), то М₁( ) М₁(F).

Следовательно, не является импликантой F, а тем более простой импликантой.

Второй подход проиллюстрируем с помощью метода построения СДНФ по ДСНФ, предложенного Квайном и усовершенствованного Мак-Класки.

Рассмотрим метод предложенный Квайном.

Пусть СДНФ для F уже получена и имеет вид

Определим, как можно вернуться от СДНФ к ДСНФ.

В ДСНФ любая конъюнкция содержит все переменные. Если в СДНФ D есть K_i, не содержащая Х_j, то можно заменить K_i на K_i( ) = .

При этом мы получим некоторую D¹ = D.

Осуществив последовательно такие разворачивания конъюнкций для D, D¹, D²,…, можно получить ДНФ, отличающуюся от ДСНФ только тем, что некоторые конъюнкции будут входить в ДНФ многократно.

Теперь, если выполнить эти действия в обратном порядке, мы получим алгоритм построения СДНФ.

Обозначим ДСНФ БФ от n переменных как D₀. Для i = 0,1,…,j,…будем получать D_i+1 из D_i, до тех пор, пока D_i+1 будет отличается от D_i.

Чтобы получить D_i+1, в D_i рассматриваются все конъюнкции с числом букв (n-i) и все пары конъюнкций вида ( ) заменяются на выражения ( ).

Затем все выражения вида ( ) и (А А) заменяются на А и на этом процесс построения D_i+1 заканчивается. (Здесь ).

Рассмотрим пример.

- дальнейшее сокращение невозможно, D₂=D₁, следовательно D₂ - СДНФ.

Но данный метод является трудоемким и может привести к тому, что не сокращения будут выполнены, так как основывается на внимательности человека.

Одна из наиболее существенных модификаций метода Квайна была предложена Мак-Класки. Основой метода попрежнему остается склеивание конъюнкций ( ), но перебор при поиске пар конъюнкций, допускающих склеивание, сокращается. (Трудоемкость работ падает.)

Рассмотрим метод Мак-Класки.

1. Каждая конъюнкция представляется n-разрядным кодом.

Значение i-ого разряда кода определяется следующим образом:	«1», если в конъюнкции есть Хi;
	«0», если в конъюнкции есть ;
	«-»,если в конъюнкции нет Хi.

Рассмотрим пример.

F(X₃X₂X₁X₀) =

K₁ К₂

Код конъюнкции K₁ представляется как (0-1-), а К₂ как (--11).

2. Коды конъюнкций разбиваются на группы с равным числом единиц в коде.

Склеиваться могут только те конъюнкции, коды которых отличаются только в одном разряде и находятся в соседних группах (с числом «1», отличающимся на одну).

Таким образом, поиск склеивающихся пар конъюнкций будет проще чем у Квайна, где проверяются все пары конъюнкций.

По Мак-Класки процесс склеивания конъюнкций для получения D₀, D₁, D₂,… представляет собой заполнение кодами конъюнкций столбцов специальной таблицы.

ДНФ D0
ДНФ D1
ДНФ D2

Каждый столбец разбивается на отдельные поля для записи групп кодов конъюнкций. При этом, в соседних полях записываются соседние группы (коды с числом единиц отличающимся на «1»).

Пример соседних групп.

0100 1000	Коды конъюнкций с одной единицей.
0011 0110 1100	Коды конъюнкций с двумя единицами.

Рассмотрим работу алгоритма на примере для БФ от трех переменных F(XYZ) с ДСНФ, равной:

Коды этих конъюнкций соответствуют наборам из М₁. (Для ДСНФ это будет всегда.): 011, 100, 101, 110, 111

Теперь строим таблицу Мак-Класки.

Шаг 1 - делим ДСНФ на группы

0	---
1	100
2	011 101 110
3	111
Число единиц в коде	D0

Шаг 2 – Выполняем склеивания между конъюнкциями соседних групп в D₀ и получаем D₁.

0	---
1	1 00	10- 1-0
2	011 101 110	-11 1-1 11-
3	111
Число единиц в коде	D0
	D1

Шаг 3 – Выполняем склеивания между конъюнкциями соседних групп в D₁ и получаем D₂.

0	---
1	1 00	10- 1-0	1-- 1--
2	011 101 110	-11 1-1 11-
3	111
Число единиц в коде	D0
	D1
	D2

Важно. Когда в наборах появились прочерки, то склеивание может выполняться только между наборами, в которых прочерки совпадают.

Все склеивания выполнены. Теперь нужно выполнить все поглощения:

Чтобы избежать потерь времени на эти действия, необходимо отмечать меткой «в» коды конъюнкций, которые не склеивались и остались после склеивания, а затем выписать их в СДНФ.

0	---
1	1 00	10- 1-0	1-- 1--	1--в
2	011 101 110	-11в 1-1 11-
3	111
Число единиц в коде	D0
	D1
	D2

В результате, после приведения подобных членов получим:

F = 1---11= X YZ.