1.1.2. Конъюнктивная совершенная нормальная форма.

Введем в рассмотрение характеристическую функцию нуля (X_n-1,…X_i,…X₁,X₀), которая равна 0 на наборе значений переменных (X_n-1,…X_i,…X₁,X₀), обозначенном  и равна 1 на всех остальных наборах.

Теперь докажем следующую теорему.

Теорема 2.

Любая бф не равная константе 1 может быть представлена в виде

F(X_n-1, … X_i, … X₁,X₀) = ₁ & ₂ & _i = i,

где M₀ - множество всех номеров наборов значений переменных, на которых F(X_n-1,…X_i,…X₁,X₀) равна 0.

Доказательство:

Возьмем произвольный набор с номером .

Пусть на этом наборе имеет место F(X_n-1,…X₁,X₀) = 1. Тогда правая часть равенства будет иметь вид 1&1&…&1=1, так как ни одна характеристическая функция не равна 0.

Следовательно, левая и правая части равны.

Если же на этом наборе F = 0, то правая часть будет иметь вид 1&1&…&0&…&1= 0, так как найдется одна , принимающая значение 0.

В результате мы получаем, что левая и правая части равны.

Рассмотрим метод получения характеристических функций нуля.

X^=1 только в том случае, если значение Х равно значению . Дизъюнкция степеней булевых переменных X_n-1,…X_i,…X₁,X₀ равна 0, если для всех Х значения степеней не равны значениям переменных. Отсюда вытекает правило получения характеристических функций нуля:

для набора значений переменных (_n-1…₁ ₀) может быть представлена как дизъюнкция степеней переменных X_n-1,…X₁,X₀ со значениями степеней соответственно (1-_n-1) … (1-₁)(1-₀).

Рассмотрим пример.

₂(X,Y,Z,W)=F₀₀₁₀(X,Y,Z,W)= X^1-0 Y^1-0 Z^1-1 W^1-0= X¹ Y¹ Z⁰ W¹=

Зная как получать характеристические функции нуля, можно сформулировать еще один способ получения выражений в алгебре Буля для таблично заданных бф не равных константе «1»:

для всех наборов значений переменных, на которых бф равна 0, выписываем характеристические функции нуля и объединяем их знаками конъюнкции.

Такое аналитическое представление называется конъюнктивной совершенной нормальной формой (КСНФ).

Таким образом, можно сделать следующий вывод:

F_М1= ДСНФ = _М0= КСНФ.

Действительно, основываясь на правилах булевой алгебры можно получить:

Решение о том, каким аналитическим представлением (ДСНФ или КСНФ) описывать булеву функцию принимается исходя из того, каких наборов меньше. Если М1 меньше, чем М0, то функцию лучше описывать с помощью ДСНФ, а если М0 меньше, чем М1, то с помощью КСНФ.

Рассмотрим пример КСНФ.

X	Y	F	F = (X1-0 Y1-1)& (X1-1 Y1-0)&( X1-1 Y1-1)= =
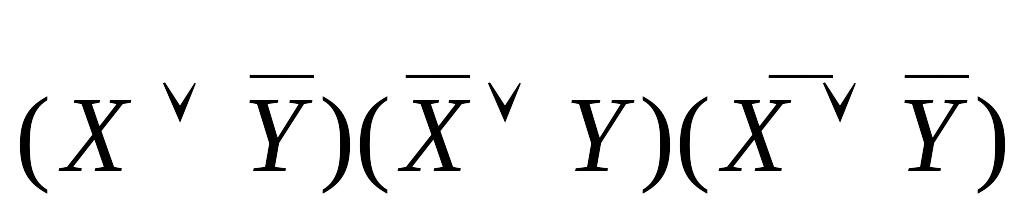
0	0	1
0	1	0
1	0	0
1	1	0

1.2. Минимизация бф.

1.2.1. Дизъюнктивная нормальная форма (днф).

Имея БФ, мы можем представить ее в виде ДСНФ, но такая форма не является единственной.

Пусть ДСНФ некоторй функции

Так как А А = А, можно представить F в виде:

Далее с, помощью скобочных преобразований, можно получить:

В полученном выражении меньше букв и операций чем в исходном.

Так как А =1, то дальнейшие преобразования приведут нас к форме:

Здесь еще меньше букв и операций. Таким образом, была выполнена минимизация исходной БФ.

Минимизация БФ подразумевает упрощение формул (при сохранении их эквивалентности) в определенном классе формул и при определенном способе подсчета сложности.

В качестве формул в теории БФ чаще всего рассматривают бесскобочные выражения вида «дизъюнкция конъюнкций» (аналог в обычной алгебре – сумма произведений), так как простые скобочные формы удобно строить из простых бесскобочных.

Ведем определения, касающиеся минимизации БФ.

Конъюнкция называется элементарной, если каждая переменная входит в нее только один раз.

Дизъюнкция элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ).

Длиной ДНФ называется число конъюнкций, из которых она состоит.

ДНФ, имеющая наименьшую длину среди всех эквивалентных, называется кратчайшей.

ДНФ, имеющая наименьшее число букв среди всех эквивалентных, называется минимальной ДНФ (МДНФ).

МДНФ может не быть кратчайшей и наоборот.

ДНФ D называется ДНФ БФ F, если М₁ для D совпадает с М₁ БФ F ( М₁(D)=М₁(F)).

БФ Ф называется импликантой БФ F, если множество наборов М₁(Ф) является частью (подмножеством) множества наборов М₁(F).

Обозначается это как: М ₁(Ф) М₁(F).

Рассмотрим пример.

Пусть

Ф₁= XY; Ф₂= YZ;

M₁(Ф₁) = = (110, 111)

M₁(Ф₂) = = (011, 111)

M₁(Ф₃) = = (101, 111)

M₁(F) = (101, 110,111)

Ф₁ и Ф₃ являются импликантами F, так как их множества М1, являются частью М1 функции F.

Ф₂ не является импликантой F, так как один набор из М1 (011), не входит в М1 функции F.

Простая импликанта - неукорачиваемая конъюнкция – из нее нельзя удалить ни одной переменной.

Конъюнкция К является простой импликантой БФ F, если:

1. К - импликанта БФ F ;

2. Любая К*, состоящая из части букв К, не является импликантой БФ F.

Рассмотрим пример простой импликанты.

X	Y	Z	F
0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	0

Предположим, что - простая импликанта БФ F.

Докажем это.

1) М₁(F) = (000,001,010,011,100)

М₁(Ф) = (000,100)

Следовательно, Ф является импликантой F.

2) Из Ф можно получить две более короткие конъюнкции: и .

M₁( ) = (000,001,100,101)

M₁( ) M₁(F) следовательно, не является импликантой F.

M₁( ) = (000,010,100,110)

M₁( ) M ₁(F) следовательно, не является импликантой F.

Следовательно из Ф нельзя удалить ни одной переменной.

Из 1) и 2) следует, что Ф простой импликантой F.

ДНФ, состоящая из всех простых импликант бф, называется сокращенной ДНФ (СДНФ).

Число букв в СДНФ может быть не только меньше, но и больше чем у ДСНФ. Слово «сокращенная» говорит о том, что в ДСНФ используются максимально укороченные (сокращенные) конъюнкции.

Если все конъюнкции ДНФ - простые мпликанты, и если удаление из нее любой конъюнкции даст ДНФ неэквивалентную исходной, то такая форма называется тупиковой ДНФ (ТДНФ).

В ТДНФ нельзя удалить ни одну букву и ни одну конъюнкцию.

Рассмотрим примеры.

Пусть - СДНФ (совокупность всех простых импликант) с

М₁(D)=(000,001,011, 111).

Покажем, что D не тднф.

Возьмем , М₁(D*) = (000,001,111).

Следовательно, D* = D, а значит D не тднф.

Теперь проверим, является ли D* - ТДНФ.

, М₁(D*¹) = (000,001) - D*¹ D, а является импликантой D.

, М₁(D*²) = (011,111) - D*² D, а является импликантой D.

Следовательно, из D* нельзя удалить ни одну букву и ни одну конъюнкцию и она является ТДНФ для D.

Аналогично можно доказать, что МДНФ обязательно является ТДНФ.

В тоже время нельзя утверждать, что любая ТДНФ является МДНФ.

У БФ может быть много ТДНФ, при этом часть из них (или все) могут быть МДНФ.

Рассмотрим пример.

Для F(x,y,z) с М₁ = (001,010,011,100,101,110) можно построить СДНФ равную

Эта бф имеет две МДНФ:

и

Кроме того, БФ имеет 3 тднф, не являющихся мднф

,

,