5. Формула полной вероятности

События образуют полную группу, если они в совокупности описывают все возможные несовместные друг с другом исходы некоторого испытания; сумма вероятностей событий полной группы равна 1. Например, испытание - бросание игральной кости. Всего исходов испытания - шесть (число выпавших очков от 1 до 6), каждый может произойти с вероятностью 1/6, сумма вероятностей всех исходов равна 1. Предположим, что событие A может наступить лишь при появлении одного из несовместных событий (гипотез) H₁, H₂, ..., H_n, образующих полную группу. Тогда вероятность события A определяется как сумма произведений вероятностей каждой из гипотез на соответствующую условную вероятность события A:

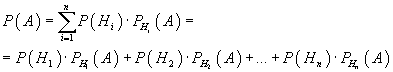
Пример 5.1

В каждой из двух урн находится 9 белых и 14 чёрных шаров. Из первой урны во вторую переложили наудачу один шар, а затем из второй урны вынули наудачу один шар. Найти вероятность того, что шар, вынутый из второй урны, окажется чёрным.

Решение Событие А - шар, вынутый из второй урны, оказался чёрным. Гипотеза Н₁ - из первой урны во вторую переложили белый шар. Р(Н₁) = 9/23. Гипотеза Н₂ - из первой урны во вторую переложили чёрный шар. Р(Н₂) = 14/23. После перекладывания во второй урне стало 24 шара. Условные вероятности события А:

По формуле полной вероятности

Свернуть

6. Формула Бейеса (Байеса)

Предположим, что событие A может наступить лишь при появлении одного из несовместных событий (гипотез) H₁, H₂, ..., H_n, образующих полную группу. Событие A уже произошло. Требуется вычислить условные вероятности гипотез (при условии, что событие А произошло).

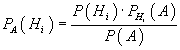
Пример 6.1

Два цеха штампуют однотипные детали. Первый цех дает 5% брака, второй - 4%. Для контроля отобрано 20 деталей с первого цеха и 10 деталей со второго. Эти детали смешаны в одну партию, и из нее наудачу извлекают одну деталь. Деталь оказалась бракованная. Какова вероятность того, что она из цеха №1?

Решение Событие А – деталь оказалась бракованной. Гипотеза Н₁ – деталь изготовлена в 1-м цехе; Р(Н₁) = 2/3 Гипотеза Н₂ – деталь изготовлена во 2-м цехе; Р(Н₂) = 1/3 Условные вероятности события А: P_H1(A)=0,05; P_H2(A)=0,04 Требуется найти вероятность первой гипотезы в предположении, что событие А уже произошло: P_A(H₁) - ? Используем формулу вероятности гипотез Бейеса, подставив в знаменатель формулу полной вероятности:

Свернуть

7. Формула Бернулли

Пусть проводятся независимые испытания (такие, при которых вероятность появления события в каждом испытании не зависит от результатов предыдущих испытаний). Далее, вероятность наступления интересующего нас события в каждом испытании постоянна и равна p. Тогда вероятность того, что рассматриваемое событие появится ровно k раз при n испытаниях (безразлично, в каком порядке), равна

В формуле Бернулли используется число сочетаний. Повторюсь, что для реализации схемы Бернулли необходимы два условия: 1) независимость проводимых испытаний; 2) p = const (постоянное значение вероятности появления события) Распределение вероятностей в схеме Бернулли - биномиальное. Наивероятнейшее число появления события (мода) при n испытаниях заключено в пределах np-q ≤ Mo ≤ np+p,

Пример 7.1

Система, составленная из четырёх блоков, работает исправно, если за рассматриваемый период выйдет из строя не более двух блоков. Найти вероятность безотказной работы системы блоков, если отказы блоков являются независимыми событиями и вероятность отказа каждого блока равна 1/8.

Решение Вероятность того, что за рассматриваемый период ни один из блоков не выйдет из строя:

Вероятность того, что за рассматриваемый период выйдет из строя один блок:

Вероятность того, что за рассматриваемый период выйдет из строя два блока:

Вероятность безотказной работы системы:

Свернуть