2. Статистическая вероятность

При статистическом определении в качестве вероятности события принимают его относительную частоту.

где m - число испытаний, в которых событие A наступило, n - общее число произведённых испытаний.

Пример 2.1

В некотором районе зарегистрировано рождение с начала года 1248 младенцев, из них 645 мальчиков. Какова вероятность рождения мальчика в данном районе?

Решение За вероятность принимаем относительную частоту рождения мальчиков. W = 645/1248 ≈ 0,517 Свернуть

3. Геометрическая вероятность

Пусть некоторая n-мерная фигура (отрезок, плоская фигура, пространственная фигура) составляет часть другой n-мерной фигуры. Если предположить, что вероятность попадания точки на эту фигуру пропорциональна её мере (длине, площади, объёму) и не зависит от взаимного расположения меньшей и большей фигур, то вероятность попадания точки на эту фигуру определяется равенствами

где l(L), s(S), v(V) - длина, площадь и объём меньшей и большей n-мерных фигур соответственно.

Пример 3.1

На плоскости начерчены две окружности радиусами 2 и 7 см соответственно, одна внутри другой. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет также и в малый круг. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади этой фигуры и не зависит от её расположения.

Решение P = s/S = πr²/πR² = 2²/7² = 4/49 ≈ 0,082 Свернуть

4. Теорема сложения и умножения вероятностей

Объединением (суммой) двух событий А и В называется событие D , происходящее тогда и только тогда, когда наступает хотя бы одно из событий А или В: D = A + B Пересечением (произведением) двух событий C и D называется событие F, происходящее тогда и только тогда, когда наступают одновременно оба события C и D: F = C · D

Пример 4.1

Пусть А, В, С, D – четыре события пространства Ω исходов эксперимента. Выразите через А, В, С, D следующие события: а) наступают все четыре события; б) наступает хотя бы одно из событий.

Решение а) A∩B∩C∩D = A·B·C·D (пересечение) б) A∪B∪C∪D = A + B + C + D (объединение) Пункт б) можно решить и другим способом, через противоположное событие. Сначала выразим событие «ни одно из событий не наступает»:

Тогда событие «наступает хотя бы одно из событий», которое является противоположным предыдущему, можно выразить так:

Свернуть

Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.

Следствие. Вероятность появления одного из нескольких попарно несовместных событий равна сумме вероятностей этих событий.

Пример 4.2

Бросается игральная кость (один раз). Найти вероятность того, что выпадет 3 очка или 5 очков.

Решение У кубика 6 граней, вероятность выпадения каждой из граней одинакова и равна 1/6. P(A + B) = P(A) + P(B) = 1/6 + 1/6 = 1/3 Свернуть

Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий за вычетом вероятности их совместного появления.

Пример 4.3

В квадрат со стороной а = 30 см случайным образом вбрасывается точка. Найдите вероятность Р того, что эта точка окажется в правой верхней четверти квадрата или не далее, чем в r = 3 см от центра квадрата.

Решение Задача интересная в том плане, что здесь также используется понятие геометрической вероятности (см. выше на этой же странице). Считаем, что точка с одинаковой вероятностью может попасть в любую область квадрата. Геометрическая вероятность находится как отношение площадей областей. Вероятность попасть в правую верхнюю четверть квадрата: Р(А) = 1/4.  Вероятность попасть в круг радиусом r = 3:

Вероятность попасть в правую верхнюю четверть круга:

Вероятность попасть хотя бы в одну из этих областей: Р(А + В) = Р(А) + Р(В) - Р(АВ)

Свернуть

Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило.

В частности, для независимых событий

События являются независимыми, если факт появления одного из них не влияет на вероятность появления другого.

Пример 4.4

В партии находятся 15 изделий: 10 изделий первого сорта, а 5 – второго. Наудачу одна за другой без возвращения в партию берутся 3 изделия. Найти вероятность того, что хотя бы одно изделие окажется второго сорта.

Решение Сначала найдём вероятность противоположного события: все три изделия, извлекаемые без возвращения из партии, оказались первого сорта. Вероятность извлечь первый раз первосортное изделие равна 10/15, второй раз условная вероятность этого события (в предположении, что первосортное изделие уже извлекли, и их стало на единицу меньше, равна 9/14, а третий раз условная вероятность в предположении, что перед этим уже два раза извлекали изделие первого сорта, равна 8/13. В соответствии с теоремой умножения вероятностей:

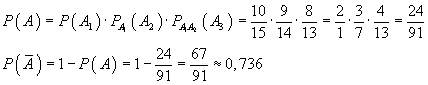
Вероятность противоположного события (хотя бы одно изделие второго сорта, т.е. либо одно, либо два, либо все три) мы нашли, отняв полученный результат от единицы. Свернуть