Пример графического решения нелинейного уравнения

В качестве уравнения, решение которого необходимо найти с точностью 0,05, возьмём следующее: sin(2x)∙ln(x-2) = 1. Ниже из­ложен ход решения этой задачи.

На рисунке 4.14 приведены первые три этапа решение этой за­дачи, выполненные в Excel по методике, изложенной выше. Заме­тим, что левая граница интервала не может равняться 2 (логарифм нуля не существует), поэтому левая граница интервала сдвинута на 0,1 вправо.

На четвёртом этапе создаём последовательность значений ар­гумента и функции F(x)=sin(2x)∙ln(x-2) -1 на выбранном интервале и с шагом, по отношению к заданной точности, пока ещё доста­точно

Рис. 4.14. Первые три этапа решения уравнения в Excel

грубым. На рисунке 4.15 приведены первые 10 членов этой последовательности.

Рис. 4.15. Первые 10 значений из 50 последовательно­стей значений аргумента и функции

На рисунке 4.16 приведён график функции, созданный на основе этих данных.

Рис. 4.16. Прикидочный график функции F(x)

Рассматривая полученный график можно сделать выводы:

1. Линия графика пересекает ось Х, причём неоднократно.

2. На графике видно, что шаг велик. Это следует из некоторой уг­ловатости линий (при правильно выбранном шаге линия графика непрерывной функции плавная, без изломов).

Так как требуется найти любое решение уравнения, то в каче­стве приближённого решения выбираем точку первого пересечения оси абсцисс x ≈ 2,5.

В качестве левой границы нового интервала возьмём прежнее значение 2,1. Учитывая, что точность решения 0,05, правую гра­ницу интервала найдём из выражения

2,1 + 0,05∙50 = 4,6.

Таким образом, новый интервал, включающий точку пересе­чения оси Х, будет равен [2.1; 4,6].

Далее, согласно методике, повторяем этапы 3 и 4 (рис. 4.17). На рис. 4.18 показан окончательный график функции вблизи точки пересечения оси Х.

Рис. 4.17 . Вторая итерация построения графика функции F(x)

Рис. 4.18. Окончательный график функции F(x) для определе­ния точки пересечения оси х

Теперь наводим указатель мыши (в программе Excel) на точку пересечения оси Х и получаем окончательный ответ (рис. 4.19).

Рис. 4.19. Публикация результатов решения задачи

5 Численные методы решения уравнений, систем уравнений и неравенств в eXcel Решение нелинейных уравнений с помощью средства «Подбор параметра»

Рассмотрим, как в Excel численно решаются нелинейные уравнения вида

f(x) = C (5.1)

Здесь С – численная константа.

Численное решение уравнения вида (5.1) рассмотрим на при­мере решения уравнения sin(2x)∙ln(x-2) = 1 с точностью 10^-4 по аргументу х.

Решение включает следую­щие этапы:

1. На рабочем листе (см. рисунок 5.1) формируется ячейка, содержащая произвольное начальное значение независимой пере­менной. Пусть это будет значение 3 (чем ближе начальное значение к искомому корню, тем лучше). В этой же ячейке будет получено решение уравнения.

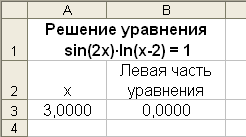
Рис. 5.1. Фрагмент рабочего листа для решения уравнения

В нашем примере – это ячейка А3. Также формируем ячейку, содержащую формулу в левой части уравнения (5.1). В нашем примере в ячейке В3 содержится формула

=SIN(2*A3)*LN(A3-2)

2. Задаём требуемую относительную точность решения уравне­ния и максимальное количество итераций. С этой целью в меню Сервис выбираем строку Параметры… и, в появив­шемся окне Параметры, выбираем вкладку Вычисления. Затем, в поле Предельное число итераций: устанавли­ваем нужное число (по умолчанию там 100), а в поле Отно­сительная погрешность: - требуемую точность (по умол­чанию там 0,001).

3. В меню Сервис выбираем строку Подбор параметра… . В появившемся окне Подбор параметра (см. рисунок 2.2) за­полняем поля. Для задачи, представленной на рис. 5.1, в поле

Рис. 5.2. Окно Подбор параметра с установленными значениями полей

Установить в ячейке: заносим адрес ячейки В3, в поле Значение: заносим константу из правой части уравнения (5.1). А в поле Изменяя значение ячейки: заносим адрес ячейки, содержащей начальное значение независимой пере­менной уравнения (5.1). Далее щёлкаем по клавише OK.

4. Появляется окно Результат подбора пара… (см. рисунок 5.3). В этом окне будут отображены результаты численного решения (если решение найдено) уравнения (5.1).

Рис. 5.3. Окно Результат подбора пара… в случае, если решение найдено

На этом этапе есть две возможности:

• щёлкнуть по кнопке OK и получить решение (в нашем примере – в ячейках А3 и В3, смотри рис. 5.4);

• щёлкнуть по кнопке Отмена, чтобы вернуть рабочий лист в прежнее состояние.

Рис. 5.4. Фрагмент рабочего листа с решением уравнения из рис.5.1

Примечание. К сожалению Excel не всегда может найти решение, по­скольку решение иногда просто не существует. В этом случае в окне Результат подбора пара… будет выдано сообщение об этом. В таких случаях можно рекомендовать следующее.

• проверить формулы и убедиться, что ячейка с форму­лой левой части уравнения (3.1) зависит от ячейки с незави­симой переменной;

• изменить начальное значение независимой переменной на зна­чение более близкое к решению и всё повторить.

• увеличить значение в поле Предельное число итераций: в окне Параметры на вкладке Вычисления (меню Сер­вис).