Типы диаграмм

Как правило, диаграммы создаются для того, чтобы доказать какое-либо утверждение или передать какое-то сообщение. Обычно само сообщение явно указано в заголовке диаграммы. Сама же диа­грамма обеспечивает наглядность этого утверждения или сообще­ния. Поэтому, если тип диаграммы выбран правильно, то утвер­ждение может стать неоспоримым фактом.

Рис. 4.1. Окно Мастер диаграмм

Практически всегда сообщением, которое требуется донести с помощью диаграммы, является сравнение. Можно выделить не­сколько общих типов сравнений.

• Сравнение одной или нескольких величин по различным категориям (регионы, месяцы, склады и т.п.). Например, диаграмма используется для сравнения объёмов продаж про­дукции по регионам.

• Сравнение данных по времени. Например, диаграмма содер­жит ежедневное количество осадков в течение месяца, а также общую тенденцию изменения количества осадков.

• Относительное сравнение. Примером может служить обыч­ная круговая диаграмма, которая показывает долю каждого сектора по отношению к целому.

• Сравнение соотношения данных. Для этого хорошо подхо­дит точечная диаграмма. Например, когда нужно показать взаимоотношения между потоками входящих и исходящих продуктов металлургического агрегата.

• Сравнение по частотам. В этом случае хорошо подходит гис­тограмма, которая отображает, например, количество студен­тов, успеваемость которых находиться в заданных пределах.

Приведём примеры диаграмм на основе одного набора данных – ежемесячное количество посетителей сайта в течении года. На рисунке 4.2 показан фрагмент рабочего листа с исходными данными, а на рисунках 4.3-4.8 – диаграммы различного типа, построенные на основе этих данных.

Легко увидеть, что наиболее просто и наглядно доносит основ-ную идею этих данных диаграммы в виде гистограммы (рис. 1.2) и график с маркерами (рис.1.4). Все остальные типы диаграмм выгля-дят существенно сложнее. Выбор же из двух диаграмм 1.2 и 1.4 определяется личными предпочтениями автора.

Рис. 4.2. Исходные данные для построения диаграмм

На практике изменить тип диаграммы очень легко, поэтому всегда можно поэкспериментировать с типами диаграмм, чтобы представить конкретный набор данных как можно более точно и ясно.

Рис. 4.3. Гистограмма на основе данных рисунка 4.2

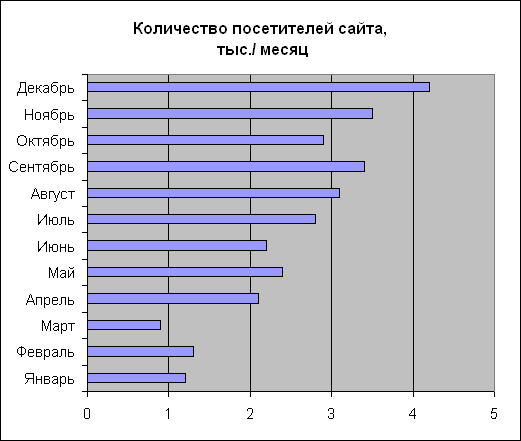
Рис. 4.4. Линейчатая диаграмма на основе данных рисунка 4.2

Рис. 4.5. График с маркерами на основе данных рисунка 4.2

Рис. 4.6. Диаграмма с областями на основе данных рисунка 4.2

Рис. 4.7. Круговая диаграмма на основе данных рисунка 4.2

Рис. 4.8. Лепестковая диаграмма на основе данных рисунка 4.2

Графики

Графики – один из самых распространёных типов диаграмм. Они применяются для отображения непрерывных данных или для отображения дискретных данных, представляющих собой функцио-нальные зависимости.

Построение графика непрерывной функции одной переменной

Построение графика непрерывной функции f(x) включает следующие этапы.

1. Определение области допустимых значений аргумента x функции (область определения функции). Эта область в про­стейшем случае может быть (-∞; ∞). Это верно, для степен­ных и ряда других функций. Для функций вида f(x) = d/(x-s), где d и s – некоторые константы, область определения не включает точку разрыва x = s (недо­пустимо деление на ноль). А вот для функции вида f(x) = ln(x-s) область определения задаётся неравенством x > s и т.д. Необходимо помнить, что график функции можно по­строить только в области её определения и не приближа­ясь близко к точкам разрыва.

2. Выбор интервала изменения аргумента x для построения графика. Этот интервал [a; b] (a –нижняя граница интервала; b – верхняя граница) выбирается в области определения функции обычно из следующих соображений:

   • если функция периодическая, то искомый интервал равен одному или двум периодам изменения функции;

   • если о функции ничего неизвестно, то интервал выбира­ется достаточно большим (по отношению к области оп­ределения функции), чтобы понять поведение функции в области её определения;

   • если важны точки пересечения осей координат, то интервал должен включать эти точки;

   • искомый интервал должен включать особые точки (точки разрыва функции).

3. Создание арифметической прогрессии из значений аргу­мента на выбранном интервале Так как функция не­прерывного типа, то количество точек на графике должно быть достаточно много (порядка 50). В ином случае график функ­ции будет искажённым. Следовательно:

• находим значение шага аргумента по формуле

Δx ≈ (b-a)/50 ;

• вводим в некоторую ячейку заголовок, например x;

• под заголовком создаём столбец значений аргумента (см. раздел 1, п.. «Создание арифметической прогрессии»).

4. Создание столбца значений функции для заданных значе­ний аргумента. Этот столбец создаём рядом со столбцом значений аргумента. Выполняем следующие действия:

   • формируем для него заголовок, например, f(x) ;

   • в первую ячейку столбца вводим формулу функции;

   • методом автозаполнения распространяем формулу на остальные ячейки столбца;

   • если в столбце появятся значения вида #ЧИСЛО! (функция не определена) или #ДЕЛ/0! (деление на ноль), то эти значения следует удалить вместе с соответствующими значениями аргумента, оставив пустые строки.

5. Выделение вместе с заголовками столбцов значений аргумента и функции и вызов окна Мастер диаграмм (рис. 4.1).

6. Выбираем в левом перечне Тип строку График, а в правом перечне Вид – Точечная диаграмма со значениями, соединёнными отрезками без маркеров (пиктограмма в правом нижнем углу перечня видов графиков). После этого щёл­каем по кнопке Далее >, пропускаем второй шаг и опять щёл­каем по кнопке Далее >.

7. На третьем шаге Мастера диаграмм устанавливаем необходимое значение атрибутов диаграммы: заголовок, линии сетки, подписи осей, легенда, цвет фона области графика. Затем щёлкаем по кнопке Далее > или по кнопке Готово.

8. На последнем шаге Мастера диаграмм, указываем на какой рабочий лист поместить диаграмму.

Примечание 1. Пункт 2 этого перечня неоднозначен. На практике действуют итеративно, то есть:

• выбирают тот или иной интервал;

• затем выполняют пункты от 3 до 6 включительно;

• далее, проверяют, удовлетворяет ли график заданным требова­ниям (например, входит ли точка пересечения линии графика оси абсцисс в этот интервал). Если требования удовлетворя­ются, то переходим к п.7, иначе возвращаемся к п. 2 и всё по­вторяется.

Примечание 2. Чтобы определить координаты любой точки линии графика следует навести курсор мыши на эту точку, после чего появится окно с сообщением о координатах.