Примеры формул
В таблице 2.3 приведены примеры формул.
Таблица 2.3
Формула |
Пояснения |
=(34+719)*29/(1-432,7) |
В ячейке с формулой отображается результат вычислений по приведённой формуле. |
=В1+ С2 |
Содержимое ячейки по адресу В1 складывается с содержимым ячейки С2. Результат отображается в ячейке с этой формулой. |
=”Часть-“ & “вторая” |
Конкатенация двух строк в результате даёт строку Часть-вторая |
=А2 & А3 |
Выполняет конкатенацию содержимого ячеек с адресоми А2 и А3. Если ячейка А2 содержит значение 123, а ячейка А3 – 456, то данная формула вернёт текстовую строку 123456 |
=6^3 |
Возводит 6 в куб. Отображаемый результат – число 216 |
=216^(1/3) |
Извлекает кубический корень из числа 216. В ячейке будет отображаться число 6. |
А1 < А2 |
В ячейке будет отображаться слово ИСТИНА, если в ячейке А1 меньше значения в ячейке А2. В ином случае будет отображаться слово ЛОЖЬ. Сравнивать можно не только числа, но и строки. Например, если ячейка А1 содержит текст Боря, а ячейка А2 – текст Клава, то отображаться в ячейке будет слово ИСТИНА |
=В5 |
В ячейке с формулой будет отображаться результат, полученный в ячейке В5. Таким образом можно переносить данные из любой ячейки в любую другую ячейку. |
=Лист4!С5
|
В ячейке с формулой будет отображаться значение ячейки С5, находящейся на листе 4. Заметим, что после имени листа ставится восклицательный знак |
=стоимость_тонны* количество_тонн |
В этой формуле используются именованные ячейки, поэтому вместо адресов употребляются имена ячеек. |
Заполнение таблиц с использование формул
Заполнение таблиц с использование формул покажем на примере заполнения треугольника Паскаля (рис. 2.2).
Рис. 2.2. Создание треугольника Паскаля в Excel
Все внутренние элементы треугольника Паскаля вычисляются по одной формуле: значение элемента равняется сумме соседних элементов в предыдущей строке. Поэтому, в ячейке G3 формула такова:
=H2+F2
Эта формула копируется во все остальные внутренние ячейки треугольника (F4, H4, E5, G5 и т.д.). Все ячейки на границе треугольника равняются единице.
Вычисление значения полинома в Excel
Вычисление значения полинома покажем на примере вычисления полинома 4-ой степени:
P(x)=a0+a1∙x+a2∙x2+a3∙x3+a4∙x4 . (2.3)
Выполним это двумя способами: первый – прямой, согласно формуле (2.3); второй – экономный, согласно формуле (2.4). В обоих случаях операция или функция возведения в степень не должна применяться.
P(x)=a0+x∙(a1+x∙(a2+x∙(a3+a4∙x))). (2.4)
Если первый способ содержит 14 операций сложения и умножения, то экономный способ (в математике его называют схемой Горнера) содержит 8 операций. На рисунке 2.3 показан рабочий лист, реализующий прямой и экономный способы вычисления полиномов.
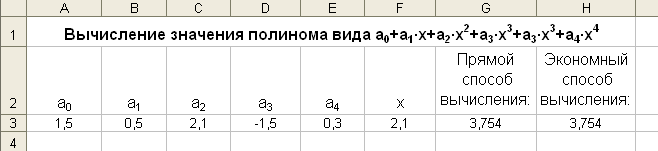
Рис. 2.3. Вычисление полинома по формулам (2.3) и (2.4)
На рисунке 2.3 ячейка G3, согласно (2.3), содержит формулу
=A3+B3*F3+C3*F3*F3+D3*F3*F3*F3+E3*F3*F3*F3*F3
Ячейка H3, согласно (2.4), содержит формулу
= A3+F3*(B3+F3*(C3+F3*(D3+E3*F3)))