Задание 7
Какими свойствами обладает данное отношение?
«x и y – любители джаза» на множестве меломанов;
Решение:
Не рефлексивно,т.к. х меломан, но не любитель джаза,то он не любители джаза, т.е. не для любого х есть пара <x,x>;
Симметрично: т.к. если x и y любители джаза,то и у и х любители джаза,т.е. для любых х и у есть пары <x,y> и <y,x>.
Транзитивно, т.к. если х и у любители джаза, и у и z любители джаза, то х и z также любители джаза , т.е. для любых пар <x,y> и <y,z> есть пара <x,z>
Не антисимметрично,т.к. обладает симметрией,т.е. если х и у любители джаза, то и у и х любители джаза, т.е. для любых х и у есть пары <x,y> и <y,x>, такие что х≠у
2. Теория графов Задание 1. Ориентированный граф
Охарактеризовать граф.
Назвать специальные вершины и рёбра.
Рассчитать полустепени вершин.
Выписать матрицы смежности, инцидентности, достижимости, связности.
Выписать цикл, цепь, простой цикл, простую цепь.
Решение:
Назовем ребра у графа:
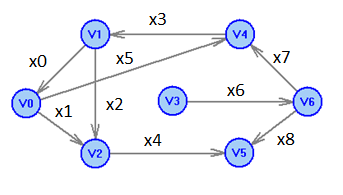
Характеристика графа:
V={V0,V1,V2,V3,V4,V5,V6}; X= {X0,X1,X2,X3,X4,X5,X6,X7,X8}
X0=<V0,V3>, X1=<V0,V2>,X2=<V1,V2>, X3=<V4,V1>,X4=<V2,V5>,X5=<V0,V4>,X6=<V3,V6>,X7=<V6,V4>,X8=<V6V5>
V3- висячая вершина
Полустепени вершин:
-(V0)=2;
-(V1)=2;
-(V2)=1;
-(V3)=1;
-(V4)=1;
-(V5)=0;
-(V6)=2
+(V0)=1; +(V1)=1; +(V2)=2; +(V3)=0; +(V4)=2; +(V5)=2; +(V6)=1 4.
Матрица смежности
|
v0 |
v1 |
v2 |
v3 |
v4 |
v5 |
v6 |
v0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
v1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
v2 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
v3 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
v4 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
v5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
v6 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
Матрица идентичности
|
x0 |
x1 |
x2 |
x3 |
х4 |
х5 |
х6 |
х7 |
x8 |
v0 |
-1 |
+1 |
0 |
0 |
0 |
+1 |
0 |
0 |
0 |
v1 |
+1 |
0 |
+1 |
-1 |
0 |
0 |
0 |
0 |
0 |
v2 |
0 |
-1 |
-1 |
0 |
+1 |
0 |
0 |
0 |
0 |
v3 |
0 |
0 |
0 |
0 |
0 |
0 |
+1 |
0 |
0 |
v4 |
0 |
0 |
0 |
+1 |
-1 |
-1 |
0 |
-1 |
0 |
v5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
v6 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
+1 |
+1 |
Матрица достижимости
|
v0 |
v1 |
v2 |
v3 |
v4 |
v5 |
v6 |
v0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
v1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
v2 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
v3 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
v4 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
v5 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
v6 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
Матрица связности
|
v0 |
v1 |
v2 |
v3 |
v4 |
v5 |
v6 |
v0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
v1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
v2 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
v3 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
v4 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
v5 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
v6 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
Простой цикл: V1 X0 V0 X5 V4 X3 V1; Цикл: нет;
Простая цепь: V1 X0 V0 X5 V4; Цепь: V1 X0 V0 X5 V4 X3 V1 X2 V2