1Множества и отношения Задание 1
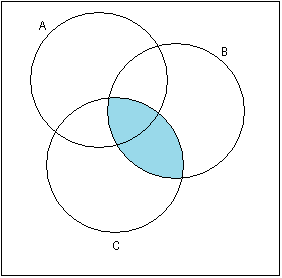
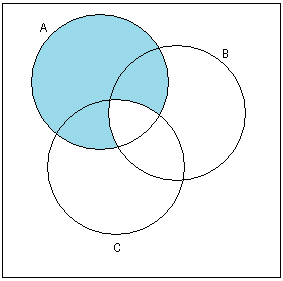
Изобразить на диаграммах Эйлера-Венна. При необходимости выражение упростить, используя тождества алгебры множеств.
2)
̚(A
B)
(
)\̚
(A
B
̚ (B
Задание 2
Доказать
с помощью основных тождеств и показать
на диаграммах Эйлера-Венна.
Решение:
(B
)
A\B
A\C
(A\B)
(A\C)
Задание 3
Доказать по определению:
Решение:
A
-
множество А включено в множество B
или совпадает с ним.
Пусть
< x,y>
(
A
B) * ( C
D)
x
(A
B), y
( C
D )
x
A , x
B, y
C , y
x
A, y
C
x
B, y
<x,y> (A * C) <x,y> (B * D) <x,y> (A*C) (B*D)
<x,y> (A*C) (B*D) <x,y> (A*C) <x,y> (B*D) x A, y C x B,y D
x
A
x
B, y
y
D
x
(A
B),y
(C
D)
<x,y>
(A
B)*(C
D)
(A B)*(C D)выполнимо тогда и только тогда,когда (A*C) (B*D)
Задание 4
Схематично изобразить геометрическое место точек прямого произведения множеств.
.
1.Строим оси OX,OY,OZ
2.В полученной системе координат строим точки и соединяем их, в результате получим 4 плоскости являющиеся прямым произведениям исходных множеств.
Задание 5
Заданы отношения р1 и р2 на множестве натуральных чисел.
Р1-“x и у кратны 2”. Р2- “ х и у кратны 8”
Вычислить:
1)р 1
р2 –х и у кратны 2 или х и у кратны 8, т.к.
8 кратно 2,то р2
р1,
следовательно р1
р2= р1;
2)р1
р2-
х и у кратны 2 и х и у кратны 8, если х и у
кратны 2 это не означает, что они кратны
8,но если х и у кратны 8 это означает, что
они кратны 2, следовательно р2
р1, следовательно р1
р2 = р2;
3)р1\р2 т.к. 8 кратно 2, то р2 р1, следовательно р1\р2= {<x,y>}| х и у кратны 2 и х и у не кратны 8};
4)р1+р2= (
р1
р2)
(р1
р2)
т.к. 8 кратно 2, то р2
р1,
следовательно
р1
= ,
а р1
р2
= р1\р2= {р1\р2= { <х,у>| х и у кратны 2 и х и
у не кратны 8};
5)р1 * р2={<x,z>
|
y
| <x,y>
р1 , <y,z>
р2 } = { <x,y>}|
x
кратен 2, z
кратен 8}
6) р1 равно р2? Нет,т.к. если х и у кратны 2, это не означает, что они кратны 8.
Задание 6
1 Дано отношение.
,
a) Построить примеры пар отношения.
b) Построить графическое представление.
c) Выяснить свойства отношения: рефлексивность, симметричность, транзитивность, антисимметричность.
Примеры пар отношений : р={<-4,-4>;<-3,-2>;<-1,-4>;<1,1>;<1,2>;<2,1>;<2,2>…}
Симметрично, т.к. если a*b- положительно, то и b*a – положительно, т.е. для любой пары <a,b> cуществует пара <b,a>. Например : для пары <1;2> есть пара <2;1>.
Транзитивно , т.к. если a*b – положительно и b*c – положительно,то a*c – всегда положительно, т.е. для любых пар < a,b> и <b,c> существует пара <a,c>. Например:для пар <-1,-2> и <-2,-4> есть пара <-1,-4>
Не антисимметрично, т.к. обладает симметрией, т.е. a*b – положительно ,то и b*a – положительно,при этом а≠b, например для пары <1;2> есть пара <2;1>