Лекция № 16 Предел функции в точке и на бесконечности. Основные теоремы о пределе функции. Односторонние пределы. Непрерывность функции. Первый и второй замечательные пределы.

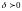Число называют пределом функции при (на плюс бесконечности), если для любого найдется число такое, что при всех , удовлетворяющих неравенству , выполняется неравенство . Обозначение :

В символах математической логики тот факт, что выглядит так .

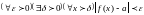Число называют пределом функции при (на минус бесконечности), если . Обозначение : .

Число называют пределом функции в точке , если . Обозначение : .

Это определение называют определением предела функции в точке на языке 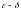, или определением предела по Коши в честь знаменитого французского математика, сформулировавшего его.

Существует другое определение предела функции в точке, сформулированное немецким математиком Гейне - определение на языке последовательностей.

Число называют пределом функции в точке , если для любой последовательности , сходящейся к , , соответственная последовательность значений функции сходится к числу .

Теорема 1. Если функция имеет предел в точке , то он единственный.

Теорема 2. Функция , имеющая предел в точке , ограничена в некоторой окрестности точки .

Теорема 3. Если , и в проколотой окрестности точки выполняется неравенство , то .

Теорема 4. Если , 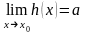и в проколотой окрестности точки выполняется неравенство , то .

Теорема 5. Если и , то в некоторой проколотой окрестности точки выполняется неравенство .

Число называют пределом справа (слева) функции в точке , если Обозначение: .

Пределы справа и слева называют односторонними пределами функции.

Теорема 6. Чтобы функция имела предел в точке , необходимо и достаточно чтобы она имела в этой точке оба односторонних предела и чтобы они были равны.

Функция называется непрерывной в точке , если .

Если в этом определении раскрыть определение предела на языке « », то получим определение: функция называется непрерывной в точке , если .

Если же раскрыть определение предела на языке последовательностей, то приходим к определению: функция называется непрерывной в точке , если для любой последовательности , сходящейся к , соответственная последовательность значений функции сходится к .

Иногда удобно формулировать определение непрерывности функции на языке приращений. Разность называют приращением аргумента в точке , а разность называют приращением функции в точке .

Функция называется непрерывной в точке , если приращение функции в точке стремится к нулю при стремлении к нулю приращения аргумента, т.е. .

Теорема 7. Если функции и непрерывны в точке , то в этой точке будут непрерывны функции 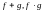, а при условии будет непрерывна функция .

Можно показать, что основные элементарные функции непрерывны в любой точке своей области определения.

Теорема 8. Пусть имеем сложную функцию 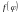. Если функция непрерывна в точке , а функция непрерывна в точке , то сложная функция непрерывна в точке .

Опираясь на теоремы 7 и 8 можно утверждать, что любая элементарная функция будет непрерывной в любой точке своей области определения.

Если предел, входящий в определение непрерывности функции в точке будет односторонним, то функция называется односторонне непрерывной в этой точке. Например, если функция непрерывна отрезке , то ясно, что в точке можно говорить лишь о непрерывности этой функции справа, а в точке - о непрерывности слева.

Теорема 9 Для непрерывности функции в точке , необходимо и достаточно, чтобы была непрерывна слева и справа от .

Теорема 10. . (первый замечательный предел).

Теорема 11. (второй замечательный предел).