Глава 8. Прямое преобразование Лапласа и операторные передаточные функции
Операционное исчисление широко применяется для решения задач электротехники.
Существует множество преобразований, используемых математиками: преобразования Лапласа, Карсона, Фурье и др. Все они имеют свои достоинства и недостатки, но преобразование Лапласа получило наибольшее распространение – MathCAD имеет встроенную поддержку данного преобразования (рис. 2.51).
Рис. 2.51
Более подробно применение операционного исчисления для решения линейных дифференциальных уравнений и систем можно рассмотреть в [14].
Рассмотрим подробно вывод операторной передаточной функции однозвенного LC-фильтра низких частот (ФНЧ) (рис. 2.52).
Рис. 2.52
На первом этапе необходимо составить систему дифференциальных уравнений, описывающих состояние ФНЧ. На вход ФНЧ подаётся гармонический сигнал. Будем использовать следующие обозначения переменных:
– входное напряжение;
– выходное
напряжение;
– ток катушки
индуктивности;
– ток конденсатора;
– ток нагрузки.
По второму закону Кирхгофа входное напряжение уравновешивается как
|
|
|
.
Согласно первому
закону Кирхгофа ток катушки индуктивности
расщепляется на ток конденсатора
и ток нагрузки
:
|
|
|
.
Известно, что ток конденсатора определяется как
|
|
|
,
а ток нагрузки по закону Ома выразим как
|
|
|
.
Система дифференциальных уравнений, описывающих состояние ФНЧ с учётом 2.7 – 2.10, выглядит следующим образом:
|
|
|
Применим к выражению 2.11 прямое преобразование Лапласа, получим систему алгебраических уравнений в изображениях и проведём алгебраические преобразования:
|
|
|
где s – оператор Лапласа.
Подставим второе уравнение системы (2.12) в первое и проведём алгебраические преобразования:
|
|
|
Операторной
передаточной функцией ФНЧ
называется отношение изображение
выходного сигнала
ко входному
:
|
|
|
.
С учётом 2.14 и 2.13 запишем выражение для операторной передаточной функции ФНЧ:
|
|
|
.
Глава 9. Обратное преобразование Лапласа и переходные функции
Рассмотрим задачу получения и анализа импульсных переходных характеристик однозвенного нагруженного Г-образного LC-фильтра низких частот (ФНЧ).
Пусть ФНЧ коммутируют на источник постоянного тока Uвх при трёх значениях сопротивления нагрузки: 10·R (нагруженный режим), 100·R (нормальный режим), 1000·R (ненагруженный режим) (рис 2.53). Необходимо с применением обратного преобразования Лапласа получить импульсные переходные характеристики для всех значений сопротивления нагрузки, определить время переходного процесса и перерегулирование. Результаты внести в таблицу.
Рис. 2.53
Вводим в MathCAD исходные данные (рис. 2.54).
Рис. 2.54
С учётом (2.15) запишем выражение для выходного напряжения ФНЧ в операторной форме
|
|
|
,
где
– операторная форма входного напряжения,
прикладываемого ступенчато при коммутации
ключа (рис. 2.53).
Упростим
в MathCAD
выражение (2.16) с применением оператора
упрощения выражений simplify
для
(рис. 2.55).
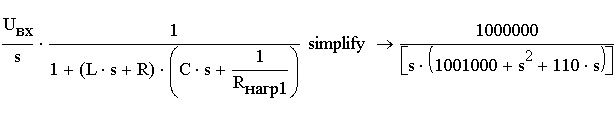
Рис. 2.55
К выражению, полученному в результате упрощения, применим обратное преобразование Лапласа с учётом нулевых начальных условий (до коммутации токи и напряжения ФНЧ равны нулю) (рис. 2.56).
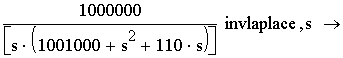
Рис. 2.56
Получаем переходную функцию ФНЧ в ненагруженном режиме:
|
|
|
и вводим её в MathCAD. Напомним, что операция присвоения в MathCAD производится как :=.
Аналогично получим в MathCAD переходные функции ФНЧ:
– в
нормальном (
),
– в
нагруженном режимах (рис. 2.57).
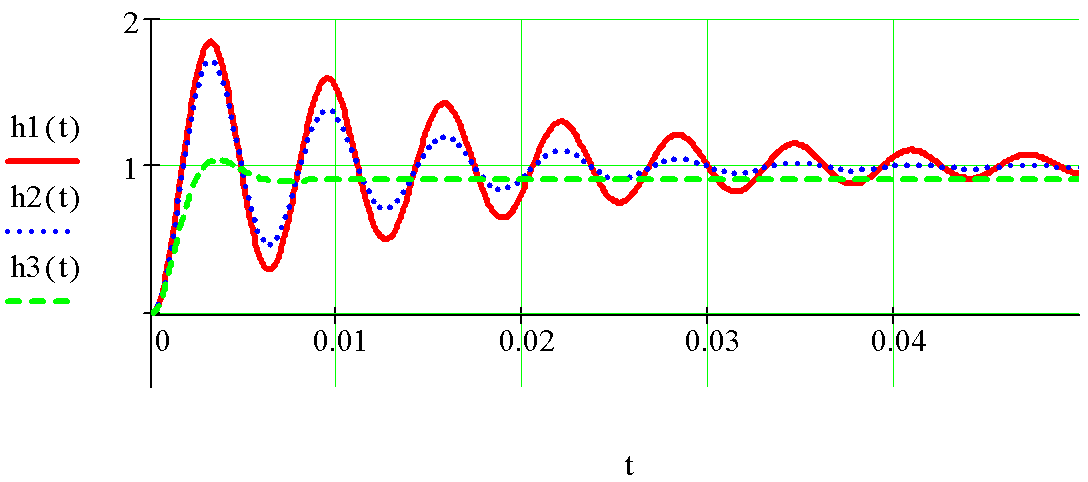
Рис. 2.57
Как
видно из рис. 2.57, переходные процессы
имеют колебательный характер с
перерегулированием и стремятся при t→∞
к установившимся значениям:
,
,
.
Переходный процесс
заканчивается, если
и
,
или, по-другому,
последний
раз входит в зону допустимых отклонений:
.
Время переходного процесса в MathCAD
можно определить графически и численно.
Переходный процесс
последний раз пересекает нижнюю границу
зоны допустимых отклонений при 0.051 с
(рис. 2.58), верхнюю – при 0.054 с (рис. 2.59),
следовательно
.
Рис. 2.58
Рис. 2.59
Аналогично в MathCAD определяем:
для время переходного процесса
;для время переходного процесса
.
Перерегулирование для переходной характеристики определим как
|
|
|
,
где
– время достижения функцией
первого максимума.
Для определения найдём в MathCAD производную по t (рис. 2.60).
Рис. 2.60
Объявим
функцию
(рис. 2.61).
Рис. 2.61
Графически
определим время
,
что соответствует
в
первом приближении (рис. 2.62).
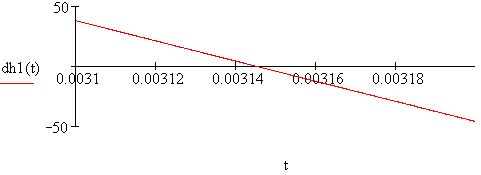
Рис. 2.62
Используя
процедуру find
и учитывая (2.18), определяем, что
перерегулирование переходной функции
составит
(рис. 2.63).
Рис. 2.63
Аналогично в MathCAD определяем:
для перерегулирование
;для перерегулирование
.
Полученные в данной главе результаты внесём в табл. 2.1.
Таблица 2.1
Показатель |
Сопротивление нагрузки |
||
|
|
|
|
Время переходного процесса |
|
|
|
Перерегулирование |
|
|
|
Как видно из табл. 2.1, с увеличением загруженности ФНЧ уменьшается время переходного процесса и перерегулирование.