
Решение.
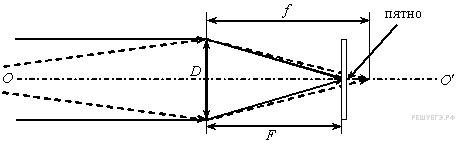
Лучи,
идущие от предмета на расстоянии d,
собираются на расстоянии f,
которое больше фокусного расстояния,
и поэтому образуют на пленке пятно
диаметром ![]() .
Из подобия треугольников получаем
соотношение:
.
Из подобия треугольников получаем
соотношение: ![]() (1).
Из
формулы тонкой линзы
(1).
Из
формулы тонкой линзы ![]() находим:
находим: ![]() (2).
Из (1) и (2) получаем окончательно:
(2).
Из (1) и (2) получаем окончательно: ![]() .
Ответ:
.
Ответ: ![]() .
.
C5 № 3035. ![]() -мезон
массой
-мезон
массой ![]() распадается
на два
-кванта.
Найдите модуль импульса одного из
образовавшихся
-квантов
в системе отсчета, где первичный
распадается
на два
-кванта.
Найдите модуль импульса одного из
образовавшихся
-квантов
в системе отсчета, где первичный ![]() -мезон
покоится.
-мезон
покоится.
Решение.
Согласно
закону сохранения импульса, фотоны от
распада покоящегося
-мезона
разлетаются в противоположные стороны
с равными по значению импульсами: ![]() .
Энергия каждого фотона связана с
импульсом соотношением
.
Энергия каждого фотона связана с
импульсом соотношением ![]() .
Согласно релятивистскому закону
сохранения энергии, в распаде
.
Согласно релятивистскому закону
сохранения энергии, в распаде ![]() .
Следовательно,
.
Следовательно, ![]() .
Ответ:
.
Ответ: ![]() .
.
C5 № 3036. В
идеальном колебательном контуре
амплитуда колебаний силы тока в катушке
индуктивности  ,
а амплитуда напряжения на конденсаторе
,
а амплитуда напряжения на конденсаторе ![]() .
В момент времени t напряжение
на конденсаторе равно
.
В момент времени t напряжение
на конденсаторе равно ![]() .
Найдите силу тока в катушке в этот
момент.
.
Найдите силу тока в катушке в этот
момент.
Решение.
В
идеальном контуре сохраняется энергия
колебаний: ![]() (1),
(1), ![]() (2).
Из
равенства (1) следует:
(2).
Из
равенства (1) следует: ![]() ,
а из (2):
,
а из (2): ![]() .
В
результате получаем:
.
В
результате получаем: 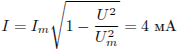 .
.
C5 № 3037. Плоская
горизонтальная фигура площадью ![]() ,
ограниченная проводящим контуром с
сопротивлением 5 Ом, находится в
однородном магнитном поле. Пока проекция
вектора магнитной индукции на вертикальную
ось Оz медленно
и равномерно возрастает от
,
ограниченная проводящим контуром с
сопротивлением 5 Ом, находится в
однородном магнитном поле. Пока проекция
вектора магнитной индукции на вертикальную
ось Оz медленно
и равномерно возрастает от ![]() до
некоторого конечного значения
до
некоторого конечного значения![]() ,
по контуру протекает заряд 0,008 Кл.
Найдите
.
,
по контуру протекает заряд 0,008 Кл.
Найдите
.
Решение.
Закон
электромагнитной индукции в случае
однородного поля ![]() (1).
В
соответствии с законом Ома
(1).
В
соответствии с законом Ома ![]() (2),
где
(2),
где ![]() —
ток в контуре за время
изменения
магнитного поля.
Исключая
из уравнений (1) и (2)
—
ток в контуре за время
изменения
магнитного поля.
Исключая
из уравнений (1) и (2) ![]() ,
получаем выражение для прошедшего
заряда
,
получаем выражение для прошедшего
заряда ![]() ,
, ![]() .
Ответ:
.
Ответ: ![]() .
.
C5 № 3038. В электрической цепи, показанной на рисунке, ЭДС источника тока равна 12 В, емкость конденсатора 2 мФ, индуктивность катушки 5 мГн, сопротивление лампы 5 Ом и сопротивление резистора 3 Ом.
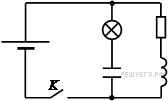
В начальный момент времени ключ К замкнут. Какая энергия выделится в лампе после размыкания ключа? Внутренним сопротивлением источника тока, и проводов пренебречь.
Решение.
Пока
ключ замкнут, через катушку течет ток I,
определяемый сопротивлением резистора:
,
конденсатор заряжен до напряжения ![]() .
Энергия электромагнитного поля в
катушке
.
Энергия электромагнитного поля в
катушке ![]() .
Энергия
электромагнитного поля в конденсаторе
.
Энергия
электромагнитного поля в конденсаторе ![]() .
После
размыкания ключа начинаются электромагнитные
колебания, и вся энергия, запасенная в
конденсаторе и катушке, выделится в
лампе и резисторе:
.
После
размыкания ключа начинаются электромагнитные
колебания, и вся энергия, запасенная в
конденсаторе и катушке, выделится в
лампе и резисторе: ![]() .
Согласно
закону Джоуля–Ленца, выделяемая в
резисторе мощность пропорциональна
его сопротивлению. Следовательно,
энергия 0,184 Дж распределится в лампе
и резисторе пропорционально их
сопротивлениям, и на лампу
приходится
.
Согласно
закону Джоуля–Ленца, выделяемая в
резисторе мощность пропорциональна
его сопротивлению. Следовательно,
энергия 0,184 Дж распределится в лампе
и резисторе пропорционально их
сопротивлениям, и на лампу
приходится ![]() .
Ответ:
.
Ответ: ![]() .
.
C5 № 3660. 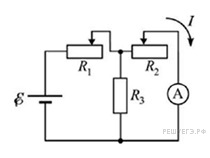 Цепь,
схема которой изображена на рисунке,
состоит из источника постоянного
напряжения с нулевым внутренним
сопротивлением, идеального амперметра,
резистора с постоянным cопротивлением
Цепь,
схема которой изображена на рисунке,
состоит из источника постоянного
напряжения с нулевым внутренним
сопротивлением, идеального амперметра,
резистора с постоянным cопротивлением ![]() и
двух реостатов, сопротивления
и
двух реостатов, сопротивления ![]() и
и ![]() которых
можно изменять. Сопротивления реостатов
меняют так, что сумма
которых
можно изменять. Сопротивления реостатов
меняют так, что сумма ![]() все
время остается неизменной (
все
время остается неизменной (![]() ).
При этом сила тока
).
При этом сила тока ![]() ,
текущего через идеальный амперметр
,
текущего через идеальный амперметр![]() ,
изменяется. При каком отношении
,
изменяется. При каком отношении ![]() сила
тока
будет
минимальной?
сила
тока
будет
минимальной?
Решение.
Обозначим
силу тока, текущего через источник и
реостат
через ![]() ,
а через резистор
—
через
,
а через резистор
—
через ![]() .
Тогда из закона сохранения электрического
заряда при постоянном токе следует,
что
.
Тогда из закона сохранения электрического
заряда при постоянном токе следует,
что ![]() .
Поскольку
реостат
и
резистор
соединены
параллельно, а амперметр идеальный, то
текущие через них токи обратно
пропорциональны их сопротивлениям:
.
Поскольку
реостат
и
резистор
соединены
параллельно, а амперметр идеальный, то
текущие через них токи обратно
пропорциональны их сопротивлениям: ![]() (закон
Ома для участка цепи).
По
закону Ома для полной цепи и формулам
для сопротивления последовательно и
параллельно соединенных резисторов:
(закон
Ома для участка цепи).
По
закону Ома для полной цепи и формулам
для сопротивления последовательно и
параллельно соединенных резисторов:
![]() .
.
Из записанных уравнений получаем:
![]() ,
и
,
и ![]() .
.
Отсюда
с учетом условия, что ![]() ,
имеем:
,
имеем:
![]() .
.
Сила
тока
будет
минимальной, если произведение ![]() примет
максимальное значение, а это будет,
очевидно, при
примет
максимальное значение, а это будет,
очевидно, при ![]() .
Таким образом, искомое отношение при
минимальной силе тока
равно
.
Таким образом, искомое отношение при
минимальной силе тока
равно![]() .
Ответ:
.
.
Ответ:
.
C5 № 3666. Колебательный
контур состоит из катушки индуктивностью ![]() и
сопротивлением
и
сопротивлением ![]() и
конденсатора ёмкостью
и
конденсатора ёмкостью ![]() .
В контуре поддерживаются незатухающие
колебания, при которых амплитуда
колебаний напряжения на конденсаторе
равна
.
В контуре поддерживаются незатухающие
колебания, при которых амплитуда
колебаний напряжения на конденсаторе
равна 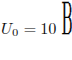 .
Какую среднюю мощность при этом потребляет
контур от внешнего источника?
.
Какую среднюю мощность при этом потребляет
контур от внешнего источника?
Решение. При незатухающих колебаниях в контуре энергия электрического поля, запасённая в конденсаторе, периодически превращается в энергию магнитного поля в катушке индуктивности:
![]()
(здесь ![]() —
амплитудное значение силы тока в
катушке).
Средняя
мощность
—
амплитудное значение силы тока в
катушке).
Средняя
мощность ![]() ,
потребляемая контуром, идёт на компенсацию
тепловых потерь в сопротивлении
,
потребляемая контуром, идёт на компенсацию
тепловых потерь в сопротивлении ![]() катушки
индуктивности контура:
катушки
индуктивности контура: ![]() ,
где
,
где ![]() —
эффективное значение силы тока в
контуре.
Из
записанных уравнений получаем:
—
эффективное значение силы тока в
контуре.
Из
записанных уравнений получаем:
![]() .
.
Ответ: ![]() .
.
C5 № 3672. Один
радиолюбитель постоянно слушал свою
любимую радиостанцию, вещающую на длине
волны ![]() в
диапазоне FM. Однажды передатчик этой
радиостанции испортился, и она перешла
на резервный передатчик, работающий в
диапазоне УКВ на частоте 73,82 МГц.
Радиолюбитель решил перестроить входной
контур своего радиоприёмника на эту
частоту, для чего он в два раза увеличил
индуктивность катушки контура, вставив
в неё ферромагнитный сердечник большего
размера. Настройка на нужную частоту у
него при этом сразу не получилась, и
пришлось вдобавок немного уменьшить
ёмкость конденсатора в контуре. На
сколько процентов была уменьшена ёмкость
этого конденсатора для точной настройки
приемника на новую частоту?
в
диапазоне FM. Однажды передатчик этой
радиостанции испортился, и она перешла
на резервный передатчик, работающий в
диапазоне УКВ на частоте 73,82 МГц.
Радиолюбитель решил перестроить входной
контур своего радиоприёмника на эту
частоту, для чего он в два раза увеличил
индуктивность катушки контура, вставив
в неё ферромагнитный сердечник большего
размера. Настройка на нужную частоту у
него при этом сразу не получилась, и
пришлось вдобавок немного уменьшить
ёмкость конденсатора в контуре. На
сколько процентов была уменьшена ёмкость
этого конденсатора для точной настройки
приемника на новую частоту?
Решение.
Длина
электромагнитной волны связана с её
частотой ![]() соотношением
соотношением ![]() ,
где
,
где ![]() —
скорость света, а
—
скорость света, а ![]() —
период колебаний. Период электромагнитных
колебаний в контуре связан с его
индуктивностью
—
период колебаний. Период электромагнитных
колебаний в контуре связан с его
индуктивностью ![]() и
ёмкостью С формулой
Томсона:
и
ёмкостью С формулой
Томсона: ![]() .
Таким образом,
.
Таким образом,
![]()
![]()
![]() .
.
Отсюда
![]() ,
и
,
и
![]() .
.
Ответ: ёмкость
конденсатора была уменьшена на ![]() .
.
C5 № 3678. В
одном из вариантов опыта, поставленного
А. К. Тимирязевым для демонстрации закона
сохранения и превращения энергии, груз
массой ![]() ,
подвешенный на шнурке, перекинутом
через блок, опускался с постоянной
скоростью
,
подвешенный на шнурке, перекинутом
через блок, опускался с постоянной
скоростью ![]() ,
вращая динамо-машину, на вал которой
был намотан другой конец шнурка.
Динамо-машина питала электрическую
лампочку, рассчитанную на напряжение
,
вращая динамо-машину, на вал которой
был намотан другой конец шнурка.
Динамо-машина питала электрическую
лампочку, рассчитанную на напряжение ![]() и
ток
и
ток ![]() ,
причем лампочка горела с нормальным
накалом. Каков был КПД
,
причем лампочка горела с нормальным
накалом. Каков был КПД ![]() превращения
механической энергии в электрическую,
выделяющуюся в лампочке в виде света и
теплоты?
превращения
механической энергии в электрическую,
выделяющуюся в лампочке в виде света и
теплоты?
Решение.
КПД
установки равен отношению электрической
мощности лампочки к механической
мощности, развиваемой при опускании
гири: ![]() .
Электрическая мощность равна
.
Электрическая мощность равна
![]() ,
,
а механическая мощность при постоянной скорости движения гири равна
![]() .
.
Таким
образом, ![]() .
Ответ: КПД
установки равен
.
Ответ: КПД
установки равен ![]() .
.
C5 № 3684. Хорошо
проводящая рамка площадью ![]() вращается
в однородном магнитном поле с индукцией
вращается
в однородном магнитном поле с индукцией  ,
перпендикулярной оси вращения рамки,
с частотой
,
перпендикулярной оси вращения рамки,
с частотой ![]() .
Скользящие контакты от рамки присоединены
к цепи, состоящей из резистора
сопротивлением
.
Скользящие контакты от рамки присоединены
к цепи, состоящей из резистора
сопротивлением ![]() ,
к которому последовательно присоединены
два параллельно соединенных резистора
сопротивлениями
,
к которому последовательно присоединены
два параллельно соединенных резистора
сопротивлениями  и
и ![]() (см.
рис.). Найти максимальную силу тока,
текущего через резистор
в
процессе вращения рамки. Индуктивностью
цепи можно пренебречь.
(см.
рис.). Найти максимальную силу тока,
текущего через резистор
в
процессе вращения рамки. Индуктивностью
цепи можно пренебречь.
Решение. При вращении рамки в магнитном поле в ней возникает ЭДС индукции, равная, по закону электромагнитной индукции Фарадея,
![]() ,
,
(здесь ![]() —
угловая частота вращения рамки).
В
цепи из резисторов, присоединенной к
рамке, под действием этой ЭДС возникает
ток, равный, согласно закону Ома для
полной цепи,
—
угловая частота вращения рамки).
В
цепи из резисторов, присоединенной к
рамке, под действием этой ЭДС возникает
ток, равный, согласно закону Ома для
полной цепи, ![]() ,
где согласно формулам для сопротивления
цепи, состоящей из последовательно и,
параллельно соединенных
резисторов,
,
где согласно формулам для сопротивления
цепи, состоящей из последовательно и,
параллельно соединенных
резисторов, ![]() .
Поскольку
падение напряжения на параллельно
соединенных резисторах
и
одинаково,
по закону Ома для участка цепи
.
Поскольку
падение напряжения на параллельно
соединенных резисторах
и
одинаково,
по закону Ома для участка цепи ![]() ,
причем в точке разветвления тока
,
причем в точке разветвления тока ![]() .
Из всех записанных уравнений следует,
что
.
Из всех записанных уравнений следует,
что
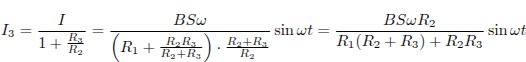 ,
,
откуда
искомая максимальная сила тока ![]() равна,
очевидно,
равна,
очевидно,
![]() .
.
Подставляя числовые данные и проверяя размерность, получаем:
![]() .
.
Ответ: ![]() .
.
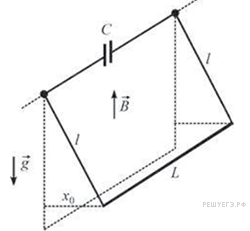
C5 № 3690. На
двух вертикальных лёгких проводах
длиной l каждый
подвешен в горизонтальном положении
массивный проводящий стержень длиной L.
Верхние концы проводов присоединены к
обкладкам конденсатора ёмкостью С.
Система находится в вертикальном
однородном магнитном поле с индукцией В (см.
рисунок). Стержень отклоняют от положения
равновесия параллельно самому себе на
небольшое расстояние ![]() и
отпускают с нулевой начальной скоростью.
Найдите зависимость от
времени t заряда q конденсатора,
считая, что в начальный момент, при
и
отпускают с нулевой начальной скоростью.
Найдите зависимость от
времени t заряда q конденсатора,
считая, что в начальный момент, при ![]() ,
конденсатор был не заряжен. Трением,
сопротивлением всех проводников и
контактов между ними, а также силами
взаимодействия токов в проводниках с
магнитным полем пренебречь.
,
конденсатор был не заряжен. Трением,
сопротивлением всех проводников и
контактов между ними, а также силами
взаимодействия токов в проводниках с
магнитным полем пренебречь.
Решение.
Согласно
условию задачи, взаимодействие токов
в проводниках с магнитным полем
пренебрежимо мало. Поэтому после
отпускания стержень будет совершать
свободные колебания, как математический
маятник, с круговой частотой ![]() ,
по закону
,
по закону ![]() ,
где x —
текущее отклонение стержня от положения
равновесия.
Поток
вектора магнитной индукции через
замкнутый контур, содержащий все
проводники и конденсатор, равен
,
где x —
текущее отклонение стержня от положения
равновесия.
Поток
вектора магнитной индукции через
замкнутый контур, содержащий все
проводники и конденсатор, равен
![]() .
.
По закону электромагнитной индукции Фарадея при колебаниях стержня в данном контуре будет возникать ЭДС индукции, равная
![]() .
.
Поскольку
сопротивлением проводников мы также
пренебрегаем, то по закону Ома для полной
цепи эта ЭДС равняется напряжению между
обкладками конденсатора: ![]() ,
откуда
,
откуда
![]() .
.
Ответ: ![]() .
.
C5 № 3697. 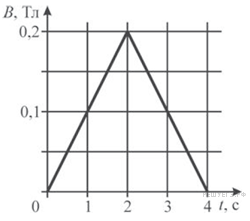 Намотанная
на каркас проволочная катушка
сопротивлением
Намотанная
на каркас проволочная катушка
сопротивлением ![]() ,
выводы которой соединены друг с другом,
помещена в однородное магнитное поле,
линии индукции которого перпендикулярны
плоскости витков катушки. Модуль вектора
магнитной индукции В поля изменяется
с течением времени t так,
как показано на графике. К моменту
времени
,
выводы которой соединены друг с другом,
помещена в однородное магнитное поле,
линии индукции которого перпендикулярны
плоскости витков катушки. Модуль вектора
магнитной индукции В поля изменяется
с течением времени t так,
как показано на графике. К моменту
времени ![]() через
катушку протек электрический заряд
через
катушку протек электрический заряд ![]() .
Сколько витков содержит катушка, если
все витки одинаковые и имеют площадь
.
Сколько витков содержит катушка, если
все витки одинаковые и имеют площадь ![]() ?
?
Решение.
В
соответствии с законом электромагнитной
индукции Фарадея, заряд, протекший через
проводящий контур, равен отношению
изменения потока вектора магнитной
индукции через площадь контура к
сопротивлению этого контура: ![]() .
Так как в данном случае контур представляет
собой проволочную катушку из Nодинаковых
витков, то
.
Так как в данном случае контур представляет
собой проволочную катушку из Nодинаковых
витков, то ![]() ,
где АВ —
изменение модуля вектора магнитной
индукции за время
,
где АВ —
изменение модуля вектора магнитной
индукции за время ![]() с.
Поэтому
с.
Поэтому![]() .
Из графика следует, что Тл. Подставляя
в полученную формулу числовые данные
и проверяя размерность, найдем:
.
Из графика следует, что Тл. Подставляя
в полученную формулу числовые данные
и проверяя размерность, найдем: ![]() .
Ответ:
.
Ответ: ![]() ,
где
,
где ![]() Тл.
Тл.
C5 № 3816. 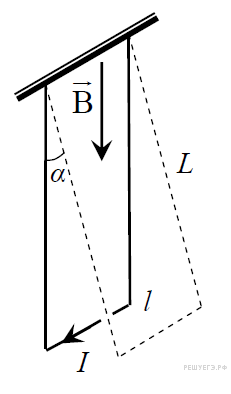 Металлический
стержень длиной l = 0,1 м и массой m =10 г ,
подвешенный на двух параллельных
проводящих нитях длиной L =1м, располагается
горизонтально в однородном магнитном
поле с индукцией B = 0,1 Тл, как показано
на рисунке. Вектор магнитной индукции
направлен вертикально. На какой
максимальный угол отклонятся от вертикали
нити подвеса, если по стержню пропустить
ток силой 10 А в течение 0,1 с? Угол α
отклонения нитей от вертикали за время
протекания тока мал.
Металлический
стержень длиной l = 0,1 м и массой m =10 г ,
подвешенный на двух параллельных
проводящих нитях длиной L =1м, располагается
горизонтально в однородном магнитном
поле с индукцией B = 0,1 Тл, как показано
на рисунке. Вектор магнитной индукции
направлен вертикально. На какой
максимальный угол отклонятся от вертикали
нити подвеса, если по стержню пропустить
ток силой 10 А в течение 0,1 с? Угол α
отклонения нитей от вертикали за время
протекания тока мал.
Решение.
При
протекании тока по стержню, находящемуся
в магнитном поле, на него действует сила
Ампера: ![]() Н,
направленная горизонтально. В соответствии
со вторым законом Ньютона эта сила
вызывает горизонтальное ускорение
стержня, которое в начальный момент
равно:
Н,
направленная горизонтально. В соответствии
со вторым законом Ньютона эта сила
вызывает горизонтальное ускорение
стержня, которое в начальный момент
равно:![]() .
Так
как за время протекания тока угол
отклонения нитей мал, влиянием подвеса
на движение стержня в горизонтальном
направлении за время t действия силы
Ампера можно пренебречь и считать это
движение равноускоренным. Следовательно,
скорость стержня в момент выключения
тока можно вычислить по формуле
.
Так
как за время протекания тока угол
отклонения нитей мал, влиянием подвеса
на движение стержня в горизонтальном
направлении за время t действия силы
Ампера можно пренебречь и считать это
движение равноускоренным. Следовательно,
скорость стержня в момент выключения
тока можно вычислить по формуле ![]() .
После
окончания действия силы Ампера стержень
движется в поле тяжести, поднимаясь на
нитях на высоту
.
После
окончания действия силы Ампера стержень
движется в поле тяжести, поднимаясь на
нитях на высоту ![]() ,
определяемую законом сохранения
энергии:
.
Отсюда
,
определяемую законом сохранения
энергии:
.
Отсюда ![]() ,
а максимальный угол отклонения нитей
подвеса от вертикали определяется
выражением
,
а максимальный угол отклонения нитей
подвеса от вертикали определяется
выражением ![]() .
Подставляя
значения физических величин, получим
.
Подставляя
значения физических величин, получим ![]() ,
т.
е.
,
т.
е. ![]() .
Ответ:
.
.
Ответ:
.
C5 № 3900. 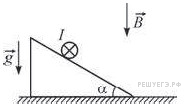 На
шероховатой плоскости, наклонённой под
углом
к
горизонту, находится однородный
цилиндрический проводник массой от
На
шероховатой плоскости, наклонённой под
углом
к
горизонту, находится однородный
цилиндрический проводник массой от ![]() г
и длиной
г
и длиной ![]() см
(см. рисунок). По проводнику пропускают
ток в направлении «от нас», за плоскость
рисунка, и вся система находится в
однородном магнитном поле с индукцией
см
(см. рисунок). По проводнику пропускают
ток в направлении «от нас», за плоскость
рисунка, и вся система находится в
однородном магнитном поле с индукцией ![]() ,
направленной вертикально вниз. При
какой силе тока
цилиндр
будет оставаться на месте, не скатываясь
с плоскости и не накатываясь на неё?
,
направленной вертикально вниз. При
какой силе тока
цилиндр
будет оставаться на месте, не скатываясь
с плоскости и не накатываясь на неё?
Решение.
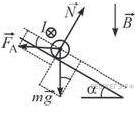 Нарисуем
силы, действующие на проводник с током:
силу тяжести
,
направленную вертикально вниз, силу
нормального давления
Нарисуем
силы, действующие на проводник с током:
силу тяжести
,
направленную вертикально вниз, силу
нормального давления ![]() .
перпендикулярную плоскости, и силу
Ампера
.
перпендикулярную плоскости, и силу
Ампера ![]() ,
равную по модулю
,
равную по модулю ![]() и
направленную в данном случае, согласно
правилу левой руки, горизонтально влево
(см. рисунок). Заметим, что все эти три
силы приложены таким образом, что они
не создают моментов сил относительно
оси цилиндра. Поэтому в равновесии сила
сухого трения цилиндра о шероховатую
наклонную плоскость децствительно
должна равняться нулю - иначе он бы
покатился.
Спроецируем
эти силы на направление вдоль плоскости
и на перпендикуляр к ней. Условия
равновесия имеют вид
и
направленную в данном случае, согласно
правилу левой руки, горизонтально влево
(см. рисунок). Заметим, что все эти три
силы приложены таким образом, что они
не создают моментов сил относительно
оси цилиндра. Поэтому в равновесии сила
сухого трения цилиндра о шероховатую
наклонную плоскость децствительно
должна равняться нулю - иначе он бы
покатился.
Спроецируем
эти силы на направление вдоль плоскости
и на перпендикуляр к ней. Условия
равновесия имеют вид ![]() .
Из
первого уравнения находим искомую
величину силы тока при равновесии
цилиндра:
.
Из
первого уравнения находим искомую
величину силы тока при равновесии
цилиндра: ![]() .
Подставляя это значение
во
второе уравнение, находим
.
Подставляя это значение
во
второе уравнение, находим ![]() (хотя
эту величину находить по условию не
требовалось).
Ответ.
(хотя
эту величину находить по условию не
требовалось).
Ответ. ![]() .
.
Тип |
Условие |
|||||||||||||||||||||||||
C5 |
C5 № 3023. Телескоп имеет объектив с фокусным расстояние 1 м и окуляр с фокусным расстоянием 5 см. Какого диаметра изображение Солнца можно получить с помощью этого телескопа, если есть возможность удалять экран от окуляра до расстояния 1,5 м? Угловой диаметр Солнца . Решение.
Спрятать решение Комментировать |
|||||||||||||||||||||||||
Тип |
Условие |
C5 |
C5 № 3024. Горизонтальный проводящий стержень прямоугольного сечения поступательно движется с ускорением вверх по гладкой наклонной плоскости в вертикальном однородном магнитном поле (см. рисунок).
По стержню протекает ток I. Угол наклона плоскости . Отношение массы стержня к его длине . Модуль индукции магнитного поля . Ускорение стержня . Чему равна сила тока в стержне? Решение. 1) На рисунке показаны силы, действующие на стержень с током:
- сила тяжести , направленная вертикально вниз; - сила реакции опоры , направленная перпендикулярно к наклонной плоскости; - сила Ампера , направленная горизонтально вправо, что вытекает из условия задачи. 2) Модуль силы Ампера , где L — длина стержня. 3) Систему отсчета, связанную с наклонной плоскостью, считаем инерциальной. Для решения задачи достаточно записать второй закон Ньютона в проекциях на ось х (см. рисунок): , где m — масса стержня. Отсюда находим . Ответ: . Спрятать решение Показать комментарии пользователей (1) |
Тип |
Условие |
C5 |
C5 № 3025. Горизонтальный проводящий стержень прямоугольного сечения поступательно движется с ускорением вверх по гладкой наклонной плоскости в вертикальном однородном магнитном поле (см. рисунок).
По стержню протекает ток . Угол наклона плоскости . Отношение массы стержня к его длине — 0,1 кг/м. Модуль индукции магнитного поля . Определите ускорение, с которым движется стержень. Решение. 1. На рисунке показаны силы, действующие на стержень с током: - сила тяжести , направленная вертикально вниз; - сила реакции опоры , направленная перпендикулярно к наклонной плоскости; - сила Ампера , направленная горизонтально вправо, что вытекает из условия задачи. 2. Модуль силы Ампера (1), где L — длина стержня. 3. Систему отсчета, связанную с наклонной плоскостью, считаем инерциальной. Для решения задачи достаточно записать второй закон Ньютона в проекциях на ось x (см. рисунок):
(2), где m — масса стержня. Отсюда находим (3). Ответ: . Спрятать решение Комментировать |
Тип |
Условие |
C5 |
C5 № 3026. В однородном магнитном поле с индукцией B, направленной вертикально вниз, равномерно вращается в горизонтальной плоскости против часовой стрелки положительно заряженный шарик массой m, подвешенный на нити длиной l (конический маятник). Угол отклонения нити от вертикали равен , скорость движения шарика равна v. Найдите заряд шарика q.
Решение. 1) На чертеже указаны силы, действующие на шарик.
2) II закон Ньютона в проекциях на оси:
3) Так как , то выражение для заряда: . Ответ: . Спрятать решение Комментировать |
Тип |
Условие |
C5 |
C5 № 3027. В однородном магнитном поле с индукцией B, направленной вертикально вниз, равномерно вращается в горизонтальной плоскости против часовой стрелки шарик, имеющий положительный заряд q. Шарик подвешен на нити длиной l (конический маятник). Угол отклонения нити от вертикали равен , скорость движения шарика равна v. Найдите массу шарика m.
Решение. 1) На чертеже указаны силы, действующие на шарик.
2) II закон Ньютона в проекциях на оси:
3) Так как , то выражение для массы: . Ответ: . Спрятать решение Комментировать |
Тип |
Условие |
C5 |
C5 № 3028. Небольшой груз, подвешенный на нити длиной 2,5 м, совершает гармонические колебания, при которых его максимальная скорость достигает 0,1 м/с. При помощи собирающей линзы с фокусным расстоянием 0,2 м изображение колеблющегося груза проецируется на экран, расположенный на расстоянии 0,6 м от линзы. Главная оптическая ось линзы перпендикулярна плоскости колебаний маятника и плоскости экрана. Определите амплитуду колебаний смещения груза на экране. Решение. Определим амплитуду колебаний. При гармонических колебаниях амплитуда, максимальная скорость и циклическая частота связаны соотношением . Отсюда Амплитуда колебаний смещения изображения груза на экране, расположенном на расстоянии b от плоскости тонкой линзы, пропорциональна амплитуде A колебаний груза, движущегося на расстоянии a от плоскости линзы: . Расстояние определяется по формуле тонкой линзы: , откуда и . Следовательно, . Ответ: . Спрятать решение Показать комментарии пользователей (1) |
Тип |
Условие |
C5 |
C5 № 3029. Небольшой груз, подвешенный на длинной нити, совершает гармонические колебания, при которых его максимальная скорость достигает 0,1 м/с. При помощи собирающей линзы с фокусным расстоянием 0,2 м изображение колеблющегося груза проецируется на экран, расположенный на расстоянии 0,5 м от линзы. Главная оптическая ось линзы перпендикулярна плоскости колебаний маятника и плоскости экрана. Максимальное смещение изображения груза на экране от положения равновесия равно . Чему равна длина нити l? Решение. При колебаниях маятника максимальная скорость груза v может быть определена из закона сохранения энергии: , где — максимальная высота подъема груза. Максимальный угол отклонения , где A — амплитуда колебаний (амплитуда смещения). Отсюда . Амплитуда колебаний смещения изображения груза на экране, расположенном на расстоянии b от плоскости тонкой линзы, пропорциональна амплитуде A колебаний груза, движущегося на расстоянии a от плоскости линзы: . Расстояние а определяется по формуле тонкой линзы: , откуда и . Следовательно, . Отсюда: . Ответ: . Спрятать решение Комментировать |
Тип |
Условие |
C5 |
C5 № 3030. Плоская рамка из провода сопротивлением 5 Ом находится в однородном магнитном поле. Проекция магнитной индукции поля на ось Ox, перпендикулярную плоскости рамки, меняется от до . За время изменения поля по рамке протекает заряд 1,6 Кл. Определите площадь рамки. Решение. Согласно закону Ома, сила тока в рамке , где ЭДС индукции . Здесь R — сопротивление рамки, S — ее площадь, — время изменения поля. Поскольку , то , . Ответ: . Спрятать решение Комментировать |
Тип |
Условие |
C5 |
C5 № 3031. Плоская рамка из провода сопротивлением 5 Ом находится в однородном магнитном поле. Проекция магнитной индукции поля на ось Ox, перпендикулярную плоскости рамки, меняется от до . Площадь рамки . Какой заряд пройдет по рамке за время изменения поля? Решение. Согласно закону Ома, сила тока в рамке , где ЭДС индукции . Здесь R — сопротивление рамки, S — ее площадь, — время изменения поля. Поскольку , то , . Ответ: . Спрятать решение Комментировать |
Тип |
Условие |
C5 |
C5 № 3032. В горизонтальное дно водоема глубиной 3 м вертикально вбита свая, полностью скрытая под водой. При угле падения солнечных лучей на поверхность воды, равном , свая отбрасывает на дно водоема тень длиной 0,8 м. Определите высоту сваи. Коэффициент преломления воды . Решение. Согласно рисунку, длина тени L определяется высотой сваи h и углом между сваей и скользящим по ее вершине лучом света: .
Этот угол является и углом преломления солнечных лучей на поверхности воды. Согласно закону преломления , , . Следовательно, , а высота сваи . Ответ: . Спрятать решение Комментировать |
Тип |
Условие |
C5 |
C5 № 3033. В горизонтальное дно водоема глубиной 3 м вертикально вбита свая, полностью скрытая под водой. Высота сваи 2 м. При угле падения солнечных лучей на поверхность воды, равном , определите длину тени сваи на дне водоёма. Коэффициент преломления воды . Решение. Согласно рисунку, длина тени L определяется высотой сваи h и углом между сваей и скользящим по ее вершине лучом света: .
Этот угол является и углом преломления солнечных лучей на поверхности воды. Согласно закону преломления , , . Следовательно, . Ответ: . Спрятать решение Комментировать |
Тип |
Условие |
C5 |
C5 № 3034. Условимся считать изображение на пленке фотоаппарата резким, если вместо идеального изображения в виде точки на пленке получается изображение пятна диаметром не более некоторого предельного значения. Поэтому, если объектив находится на фокусном расстоянии от пленки, то резкими считаются не только бесконечно удаленные предметы, но и все предметы, находящиеся дальше некоторого расстояния d. Оцените предельный размер пятна, если при фокусном расстоянии объектива 50 мм и диаметре входного отверстия 5 мм резкими оказались все предметы, находившиеся на расстояниях более 5 м от объектива. Сделайте рисунок, поясняющий образование пятна. Решение.
Лучи, идущие от предмета на расстоянии d, собираются на расстоянии f, которое больше фокусного расстояния, и поэтому образуют на пленке пятно диаметром . Из подобия треугольников получаем соотношение: (1). Из формулы тонкой линзы находим: (2). Из (1) и (2) получаем окончательно: . Ответ: . Спрятать решение Комментировать |
Тип |
Условие |
C5 |
C5 № 3035. -мезон массой распадается на два -кванта. Найдите модуль импульса одного из образовавшихся -квантов в системе отсчета, где первичный -мезон покоится. Решение. Согласно закону сохранения импульса, фотоны от распада покоящегося -мезона разлетаются в противоположные стороны с равными по значению импульсами: . Энергия каждого фотона связана с импульсом соотношением . Согласно релятивистскому закону сохранения энергии, в распаде . Следовательно, . Ответ: . Спрятать решение Комментировать |
Тип |
Условие |
C5 |
C5 № 3036. В идеальном колебательном контуре амплитуда колебаний силы тока в катушке индуктивности , а амплитуда напряжения на конденсаторе . В момент времени t напряжение на конденсаторе равно . Найдите силу тока в катушке в этот момент. Решение. В идеальном контуре сохраняется энергия колебаний: (1), (2). Из равенства (1) следует: , а из (2): . В результате получаем: . Спрятать решение Комментировать |
Тип |
Условие |
C5 |
C5 № 3037. Плоская горизонтальная фигура площадью , ограниченная проводящим контуром с сопротивлением 5 Ом, находится в однородном магнитном поле. Пока проекция вектора магнитной индукции на вертикальную ось Оz медленно и равномерно возрастает от до некоторого конечного значения , по контуру протекает заряд 0,008 Кл. Найдите . Решение. Закон электромагнитной индукции в случае однородного поля (1). В соответствии с законом Ома (2), где — ток в контуре за время изменения магнитного поля. Исключая из уравнений (1) и (2) , получаем выражение для прошедшего заряда , . Ответ: . Спрятать решение Показать комментарии пользователей (2) |
Тип |
Условие |
C5 |
C5 № 3038. В электрической цепи, показанной на рисунке, ЭДС источника тока равна 12 В, емкость конденсатора 2 мФ, индуктивность катушки 5 мГн, сопротивление лампы 5 Ом и сопротивление резистора 3 Ом.
В начальный момент времени ключ К замкнут. Какая энергия выделится в лампе после размыкания ключа? Внутренним сопротивлением источника тока, и проводов пренебречь. Решение. Пока ключ замкнут, через катушку течет ток I, определяемый сопротивлением резистора: , конденсатор заряжен до напряжения . Энергия электромагнитного поля в катушке . Энергия электромагнитного поля в конденсаторе . После размыкания ключа начинаются электромагнитные колебания, и вся энергия, запасенная в конденсаторе и катушке, выделится в лампе и резисторе: . Согласно закону Джоуля–Ленца, выделяемая в резисторе мощность пропорциональна его сопротивлению. Следовательно, энергия 0,184 Дж распределится в лампе и резисторе пропорционально их сопротивлениям, и на лампу приходится . Ответ: . Спрятать решение Показать комментарии пользователей (2) |
Тип |
Условие |
C5 |
C5 № 3081.
В
однородном магнитном поле с индукцией Показать решение Комментировать |
Тип |
Условие |
C5 |
C5 № 3660. Цепь, схема которой изображена на рисунке, состоит из источника постоянного напряжения с нулевым внутренним сопротивлением, идеального амперметра, резистора с постоянным cопротивлением и двух реостатов, сопротивления и которых можно изменять. Сопротивления реостатов меняют так, что сумма все время остается неизменной ( ). При этом сила тока , текущего через идеальный амперметр , изменяется. При каком отношении сила тока будет минимальной? Решение. Обозначим силу тока, текущего через источник и реостат через , а через резистор — через . Тогда из закона сохранения электрического заряда при постоянном токе следует, что . Поскольку реостат и резистор соединены параллельно, а амперметр идеальный, то текущие через них токи обратно пропорциональны их сопротивлениям: (закон Ома для участка цепи). По закону Ома для полной цепи и формулам для сопротивления последовательно и параллельно соединенных резисторов: . Из записанных уравнений получаем: , и . Отсюда с учетом условия, что , имеем: . Сила тока будет минимальной, если произведение примет максимальное значение, а это будет, очевидно, при . Таким образом, искомое отношение при минимальной силе тока равно . Ответ: . Спрятать решение Комментировать |
Тип |
Условие |
C5 |
C5 № 3666. Колебательный контур состоит из катушки индуктивностью и сопротивлением и конденсатора ёмкостью . В контуре поддерживаются незатухающие колебания, при которых амплитуда колебаний напряжения на конденсаторе равна . Какую среднюю мощность при этом потребляет контур от внешнего источника? Решение. При незатухающих колебаниях в контуре энергия электрического поля, запасённая в конденсаторе, периодически превращается в энергию магнитного поля в катушке индуктивности:
(здесь — амплитудное значение силы тока в катушке). Средняя мощность , потребляемая контуром, идёт на компенсацию тепловых потерь в сопротивлении катушки индуктивности контура: , где — эффективное значение силы тока в контуре. Из записанных уравнений получаем: . Ответ: . Спрятать решение Комментировать |
Тип |
Условие |
C5 |
C5 № 3672. Один радиолюбитель постоянно слушал свою любимую радиостанцию, вещающую на длине волны в диапазоне FM. Однажды передатчик этой радиостанции испортился, и она перешла на резервный передатчик, работающий в диапазоне УКВ на частоте 73,82 МГц. Радиолюбитель решил перестроить входной контур своего радиоприёмника на эту частоту, для чего он в два раза увеличил индуктивность катушки контура, вставив в неё ферромагнитный сердечник большего размера. Настройка на нужную частоту у него при этом сразу не получилась, и пришлось вдобавок немного уменьшить ёмкость конденсатора в контуре. На сколько процентов была уменьшена ёмкость этого конденсатора для точной настройки приемника на новую частоту? Решение. Длина электромагнитной волны связана с её частотой соотношением , где — скорость света, а — период колебаний. Период электромагнитных колебаний в контуре связан с его индуктивностью и ёмкостью С формулой Томсона: . Таким образом, . Отсюда , и . Ответ: ёмкость конденсатора была уменьшена на . Спрятать решение Комментировать |
Тип |
Условие |
C5 |
C5 № 3678. В одном из вариантов опыта, поставленного А. К. Тимирязевым для демонстрации закона сохранения и превращения энергии, груз массой , подвешенный на шнурке, перекинутом через блок, опускался с постоянной скоростью , вращая динамо-машину, на вал которой был намотан другой конец шнурка. Динамо-машина питала электрическую лампочку, рассчитанную на напряжение и ток , причем лампочка горела с нормальным накалом. Каков был КПД превращения механической энергии в электрическую, выделяющуюся в лампочке в виде света и теплоты? Решение. КПД установки равен отношению электрической мощности лампочки к механической мощности, развиваемой при опускании гири: . Электрическая мощность равна , а механическая мощность при постоянной скорости движения гири равна . Таким образом, . Ответ: КПД установки равен . Спрятать решение Комментировать |
Тип |
Условие |
C5 |
C5 № 3684. Хорошо проводящая рамка площадью вращается в однородном магнитном поле с индукцией , перпендикулярной оси вращения рамки, с частотой . Скользящие контакты от рамки присоединены к цепи, состоящей из резистора сопротивлением , к которому последовательно присоединены два параллельно соединенных резистора сопротивлениями и (см. рис.). Найти максимальную силу тока, текущего через резистор в процессе вращения рамки. Индуктивностью цепи можно пренебречь. Решение. При вращении рамки в магнитном поле в ней возникает ЭДС индукции, равная, по закону электромагнитной индукции Фарадея, , (здесь — угловая частота вращения рамки). В цепи из резисторов, присоединенной к рамке, под действием этой ЭДС возникает ток, равный, согласно закону Ома для полной цепи, , где согласно формулам для сопротивления цепи, состоящей из последовательно и, параллельно соединенных резисторов, . Поскольку падение напряжения на параллельно соединенных резисторах и одинаково, по закону Ома для участка цепи , причем в точке разветвления тока . Из всех записанных уравнений следует, что , откуда искомая максимальная сила тока равна, очевидно, . Подставляя числовые данные и проверяя размерность, получаем: . Ответ: . Спрятать решение Комментировать |
Тип |
Условие |
C5 |
C5 № 3690. На двух вертикальных лёгких проводах длиной l каждый подвешен в горизонтальном положении массивный проводящий стержень длиной L. Верхние концы проводов присоединены к обкладкам конденсатора ёмкостью С. Система находится в вертикальном однородном магнитном поле с индукцией В (см. рисунок). Стержень отклоняют от положения равновесия параллельно самому себе на небольшое расстояние и отпускают с нулевой начальной скоростью. Найдите зависимость от времени t заряда q конденсатора, считая, что в начальный момент, при , конденсатор был не заряжен. Трением, сопротивлением всех проводников и контактов между ними, а также силами взаимодействия токов в проводниках с магнитным полем пренебречь.
Решение. Согласно условию задачи, взаимодействие токов в проводниках с магнитным полем пренебрежимо мало. Поэтому после отпускания стержень будет совершать свободные колебания, как математический маятник, с круговой частотой , по закону , где x — текущее отклонение стержня от положения равновесия. Поток вектора магнитной индукции через замкнутый контур, содержащий все проводники и конденсатор, равен . По закону электромагнитной индукции Фарадея при колебаниях стержня в данном контуре будет возникать ЭДС индукции, равная . Поскольку сопротивлением проводников мы также пренебрегаем, то по закону Ома для полной цепи эта ЭДС равняется напряжению между обкладками конденсатора: , откуда . Ответ: . Спрятать решение Показать комментарии пользователей (2) |
Тип |
Условие |
C5 |
C5 № 3697. Намотанная на каркас проволочная катушка сопротивлением , выводы которой соединены друг с другом, помещена в однородное магнитное поле, линии индукции которого перпендикулярны плоскости витков катушки. Модуль вектора магнитной индукции В поля изменяется с течением времени t так, как показано на графике. К моменту времени через катушку протек электрический заряд . Сколько витков содержит катушка, если все витки одинаковые и имеют площадь ? Решение. В соответствии с законом электромагнитной индукции Фарадея, заряд, протекший через проводящий контур, равен отношению изменения потока вектора магнитной индукции через площадь контура к сопротивлению этого контура: . Так как в данном случае контур представляет собой проволочную катушку из Nодинаковых витков, то , где АВ — изменение модуля вектора магнитной индукции за время с. Поэтому . Из графика следует, что Тл. Подставляя в полученную формулу числовые данные и проверяя размерность, найдем: . Ответ: , где Тл. Спрятать решение Комментировать |
Тип |
Условие |
C5 |
C5 № 3816. Металлический стержень длиной l = 0,1 м и массой m =10 г , подвешенный на двух параллельных проводящих нитях длиной L =1м, располагается горизонтально в однородном магнитном поле с индукцией B = 0,1 Тл, как показано на рисунке. Вектор магнитной индукции направлен вертикально. На какой максимальный угол отклонятся от вертикали нити подвеса, если по стержню пропустить ток силой 10 А в течение 0,1 с? Угол α отклонения нитей от вертикали за время протекания тока мал. Решение. При протекании тока по стержню, находящемуся в магнитном поле, на него действует сила Ампера: Н, направленная горизонтально. В соответствии со вторым законом Ньютона эта сила вызывает горизонтальное ускорение стержня, которое в начальный момент равно: . Так как за время протекания тока угол отклонения нитей мал, влиянием подвеса на движение стержня в горизонтальном направлении за время t действия силы Ампера можно пренебречь и считать это движение равноускоренным. Следовательно, скорость стержня в момент выключения тока можно вычислить по формуле . После окончания действия силы Ампера стержень движется в поле тяжести, поднимаясь на нитях на высоту , определяемую законом сохранения энергии: . Отсюда , а максимальный угол отклонения нитей подвеса от вертикали определяется выражением . Подставляя значения физических величин, получим , т. е. . Ответ: . Спрятать решение Комментировать |
Тип |
Условие |
C5 |
C5 № 3900. На шероховатой плоскости, наклонённой под углом к горизонту, находится однородный цилиндрический проводник массой от г и длиной см (см. рисунок). По проводнику пропускают ток в направлении «от нас», за плоскость рисунка, и вся система находится в однородном магнитном поле с индукцией , направленной вертикально вниз. При какой силе тока цилиндр будет оставаться на месте, не скатываясь с плоскости и не накатываясь на неё? Решение. Нарисуем силы, действующие на проводник с током: силу тяжести , направленную вертикально вниз, силу нормального давления . перпендикулярную плоскости, и силу Ампера , равную по модулю и направленную в данном случае, согласно правилу левой руки, горизонтально влево (см. рисунок). Заметим, что все эти три силы приложены таким образом, что они не создают моментов сил относительно оси цилиндра. Поэтому в равновесии сила сухого трения цилиндра о шероховатую наклонную плоскость децствительно должна равняться нулю - иначе он бы покатился. Спроецируем эти силы на направление вдоль плоскости и на перпендикуляр к ней. Условия равновесия имеют вид . Из первого уравнения находим искомую величину силы тока при равновесии цилиндра: . Подставляя это значение во второе уравнение, находим (хотя эту величину находить по условию не требовалось). Ответ. . Спрятать решение Показать комментарии пользователей (1) |
Тип |
Условие |
C5 |
C5 № 3901. Решение.
|

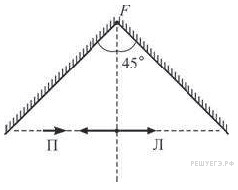 Два
плоских зеркала образуют прямой
двугранный угол, перпендикулярно
биссектрисе которого расположена
небольшая собирающая линза Л, а её
фокус F находится
в вершине угла (см.
рисунок).
В плоскости линзы рядом с ней находится
небольшой предмет П. Постройте
изображение предмета, которое получится
в результате двух отражений от зеркал
и последующего преломления света
линзой. На каком расстоянии от предмета
будет находиться его изображение?
Два
плоских зеркала образуют прямой
двугранный угол, перпендикулярно
биссектрисе которого расположена
небольшая собирающая линза Л, а её
фокус F находится
в вершине угла (см.
рисунок).
В плоскости линзы рядом с ней находится
небольшой предмет П. Постройте
изображение предмета, которое получится
в результате двух отражений от зеркал
и последующего преломления света
линзой. На каком расстоянии от предмета
будет находиться его изображение?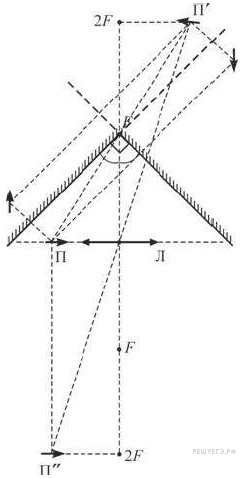 Построим
вначале изображение предмета П после
двух отражений от плоских зеркал. Как
видно из построения на рисунке, предмет
как бы «отражается» относительно
вершины прямого угла, и его мнимое
перевёрнутое изображение П' находится
на расстоянии 2F от плоскости линзы Л.
Далее построим изображение П"
«предмета» П' в линзе - оно действительное,
перевёрнутое относительно П' (и прямое
относительно предмета П) и находится
также на расстоянии 2F от линзы. Таким
образом, изображение П" прямое,
действительное и находится на расстоянии
2F от предмета П - ниже его, на линии,
параллельной биссектрисе угла из
зеркал.
Ответ:
см. рисунок; изображение П" прямое,
действительное и находится на расстоянии
2F от предмета П - ниже его, на линии,
параллельной биссектрисе угла из
зеркал.
Построим
вначале изображение предмета П после
двух отражений от плоских зеркал. Как
видно из построения на рисунке, предмет
как бы «отражается» относительно
вершины прямого угла, и его мнимое
перевёрнутое изображение П' находится
на расстоянии 2F от плоскости линзы Л.
Далее построим изображение П"
«предмета» П' в линзе - оно действительное,
перевёрнутое относительно П' (и прямое
относительно предмета П) и находится
также на расстоянии 2F от линзы. Таким
образом, изображение П" прямое,
действительное и находится на расстоянии
2F от предмета П - ниже его, на линии,
параллельной биссектрисе угла из
зеркал.
Ответ:
см. рисунок; изображение П" прямое,
действительное и находится на расстоянии
2F от предмета П - ниже его, на линии,
параллельной биссектрисе угла из
зеркал.