26. Основні поняття теорії графів: маршрут, довжина маршруту, цикл, простий та елементарний ланцюг.

Нехай G – неорієнтований граф. Маршрутом в графі G називається така послідовність (кінцева або нескінченна) ребер a₁, a₂, ... a_n..., що кожні два сусідні ребра a_i та a_i+1 мають загальну інцидентну вершину. Одне і те ж ребро може зустрічатися в маршруті кілька разів. У кінцевому маршруті (a₁, a₂, ... a_n) є перше ребро a₁ і останнє ребро a_n. Вершина x₁, інцидентна ребру a₁, але не інцидентна ребру a₂, називається початком маршруту, а вершина x_n, інцидентна ребру a_n, але не інцидентна ребру a_n-1, називається кінцем маршруту.

Довжиною маршруту називається число ребер, що входять в маршрут, причому кожне ребро рахується стільки раз, скільки воно входить в даний маршрут.

Замкнутий маршрут називається циклом.

Маршрут (цикл), в якому всі ребра різні, називається простим ланцюгом (циклом). Маршрут (цикл), в якому всі вершини (окрім першої і останньої) різні, називається елементарним ланцюгом (циклом).

27. Основні поняття теорії графів: шлях, довжина шляху, простий та елементарний контур. Поняття зв’зного та навантаженого графу, довжини шляху, матриця вагів.

Шляхом в орієнтованому графі називається послідовність дуг, в якій кінцева вершина всякої дуги, відмінної від останньої, є початковою вершиною наступної дуги.

Число дуг шляху називається довжиною шляху.

Шлях називається контуром, якщо його початкова вершина співпадає з кінцевою вершиною.

Шлях (контур), в якому всі дуги різні, називається простим.

Шлях (контур), в якому всі вершини, окрім першої і останньої, різні, називається елементарним.

Поняттям ребра, маршруту, ланцюга, циклу в неорієнтованому графі відповідають поняття дуги, шляху, орієнтованого ланцюга, контура в орієнтованому графі.

Неорієнтований граф	Орієнтований граф
ребро маршрут цикл	дуга шлях контур

Граф називається зв’язним, якщо кожна пара різних вершин може бути сполучена, принаймні, одним ланцюгом.

Орієнтований граф називається навантаженим, якщо дугам цього графа поставлені у відповідність ваги, так що дузі (x_i ,x_j) зіставлено деяке число c(x_i, x_j) = c_ij, зване довжиною (або вагою, або вартістю дуги). Довжиною (або вагою або вартістю) шляху s, що складається з деякої послідовності дуг (x_i, x_j), называется число l(s), що дорівнює сумі довжин дуг, що входять в цей шлях, тобто

l(s) =

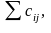
причому підсумовування ведеться по всіх дугах (x_i, x_j) s.

Матриця C = (c_ij) називається матрицею довжин дуг або матрицею вагів.

28. Основні поняття теорії графів: підгрф неорієнтованого графа, власний підграф, компонента зв’язності неорієнтованого графа, неорієнтоване дерево, дерево-остов.

Підграфом неорієнтованого графа G називається граф, всі вершини і ребра якого містяться серед вершин і ребер графа G. Підграф називається власним, якщо він відмінний від самого графа. Аналогічно визначається підграф орієнтованого графа.

Компонентою зв’язності неорієнтованого графа називається його зв’язний підграф, що не є власним підграфом ніякого іншого зв’язного підграфа даного графа.

Неорієнтованим деревом (або просто деревом) називається зв’язний граф без циклів.

Остовним деревом (деревом-остовом, покриваючим деревом, скелетним деревом) зв’язного графа G називається будь-який його підграф, що містить всі вершини графа G і що є деревом.

29. Алгоритм побудови мінімального покриваючого дерева (алгоритму Краскала).

Нехай G – зв’язний навантажений граф. Завдання побудови мінімального остовного дерева полягає в тому, щоб з множини остовних дерев знайти таке, у якого сума довжин ребер мінімальна.

Приведемо типові випадки, коли виникає необхідність побудови мінімального остовного дерева графа:

а) Необхідно з’єднати n міст залізничними лініями (або автомобільними дорогами, лініями електропередач, мережею трубопроводів і так далі) так, щоб сумарна довжина ліній або вартість була б мінімальною.

б) Потрібно побудувати схему електричної (комп’ютерної) мережі, в якої клеми (вузли мережі) повинні бути сполучені за допомогою проводів найменшої загальної довжини.

Задачу побудови мінімального дерева-остову можна вирішити за допомогою алгоритму Краскала. Приведемо опис алгоритму по кроках.

Крок 1. Відсортуємо ребра графа по неубуванню вагів.

Крок 2. Вважаємо, що кожна вершина відноситься до своєї компоненти зв’язності.

Крок 3. Проходимо ребра в «відсортованому» порядку. Для кожного ребра виконуємо наступну перевірку:

а) якщо вершини, що сполучаються даним ребром, лежать в різних компонентах зв’язності, то об’єднуємо ці компоненти в одну, а дане ребро додаємо до мінімального дерева-остову;

б) якщо вершини, що сполучаються даним ребром, лежать в одній компоненті зв’язності, то виключаємо ребро з розгляду, оскільки при включенні даного ребра утворюється цикл.

Крок 4. Якщо є ще нерозглянуті ребра і не всі компоненти зв’язності об’єднані в одну, то переходимо до кроку 3, інакше алгоритм завершує роботу:

а) якщо при цьому проглянуті всі ребра, але не всі компоненти зв’язності об’єднані в одну, то для початкового графа неможливо побудувати покриваюче дерево;

б) якщо проглянуті всі ребра, і всі компоненти зв’язності об’єднані в одну, то для початкового графа побудовано мінімальне покриваюче дерево.