
- •16. Встановлення найбільш економічного об’єму партії у детермінованій моделі без дефіциту (формулою Уілсона).
- •17. Статистична детермінована модель з дефіцитом.
- •20. Встановлення оптимального об’єму партії в задачі з дефіцитом.
- •21. Стохастичні моделі.
- •22. Встановлення функції сумарних витрат в стохастичних моделях управління запасами з випадковим попитом.
- •23. Сутність задачі управління запасами у стохастичних моделях.
- •24. Стохастичні моделі управління запасами з фіксованим часом затримки поставок.
- •25. Основні поняття теорії графів: граф, ребро, дуги, орієнтований, змішаний та зважений граф. Матриця суміжності та інцидентності, правила їх побудови та використання.
- •26. Основні поняття теорії графів: маршрут, довжина маршруту, цикл, простий та елементарний ланцюг.
- •27. Основні поняття теорії графів: шлях, довжина шляху, простий та елементарний контур. Поняття зв’зного та навантаженого графу, довжини шляху, матриця вагів.
- •28. Основні поняття теорії графів: підгрф неорієнтованого графа, власний підграф, компонента зв’язності неорієнтованого графа, неорієнтоване дерево, дерево-остов.
- •29. Алгоритм побудови мінімального покриваючого дерева (алгоритму Краскала).
- •30. Пошук шляхів із заданою кількістю дуг між вузлами мережі.
- •Пошук шляхів із заданою кількістю дуг
24. Стохастичні моделі управління запасами з фіксованим часом затримки поставок.
В розглянутих вище ідеалізованих моделях управляння запасами передбачалось, що поповнення запасів відбувається практично миттєво. Проте в багатьох задачах час затримки поставок може виявитись на стільки значним, що його необхідно враховувати в моделі.
Нехай за час затримок поставок Ө вже замовлено n партій по одній в кожний із n періодів тривалістю T=Ө/n.
Позначимо:
sнз – початковий рівень запасу (до початку першого періоду);
si – запас за і-й період;
ri – попит за і-й період;
qi – поповнення запасу за і-й період.
Тоді
до кінця n-го
періоду на склад поступить
 одиниць продукту, а витрачено буде
одиниць продукту, а витрачено буде
 одиниць, тобто
одиниць, тобто
 ,
(2.39)
,
(2.39)
або
 (2.40)
(2.40)
де
 ,
(2.41)
,
(2.41)
 .
(2.42)
.
(2.42)
Потрібно знайти оптимальний об’єм партії замовлення, який необхідно зробити за останній n-й період, попередній надходженню зробленого раніше замовлення.
Математичне очікування сумарних витрат в цьому випадку встановлюється за формулою (2.28), а оптимальний запас s знаходиться за формулою (2.30), тобто
F(s0) < p < F(s0 +1) (2.43)
Знайшовши оптимальний запас s0 та знаючи q1, q2, …,qn-1, можна розрахувати qn за формулою (2.41), тобто
 .
(2.44)
.
(2.44)
25. Основні поняття теорії графів: граф, ребро, дуги, орієнтований, змішаний та зважений граф. Матриця суміжності та інцидентності, правила їх побудови та використання.
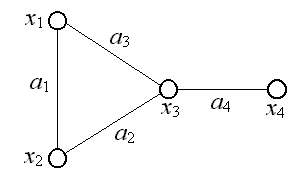
Графом G = (X, А) називається пара об’єктів X = {x1, x2 ., xn} і А = {a1, a2 ., am}, де X – множина вершин, а A – множина ребер графа. Якщо ребра з множини A орієнтовані, то вони називаються дугами, а граф називають орієнтованим. Якщо ребра не мають орієнтації, то граф називають неорієнтованим. Інакше граф є змішаним. На рис.4.1–4.6 приведені неорієнтований і орієнтований графи відповідно.
|
X = {x1, x2, x3, x4}, A = {a1, a2, a3, a4}.
|
|
X = {x1, x2, x3, x4}, A = {a1 = (x1 , x2 ), a2 = (x1 , x3 ), a3 = (x3 , x4 ), a4 = (x3 , x2 )}. |
Якщо зіставити кожному ребру число з множини С, тоді граф називають зваженим.
Граф можна задати матрицями суміжності і інцидентності. Елементи матриці суміжності S графа задаються так:
|
якщо існує ребро (дуга), що сполучає вершини хi та xj;
інакше, |
(i, j=1, 2,…, n). |
Елементи
матриці інцидентності
 для графа G,
що складається з n
вершин
і m
дуг,
визначаються як:
для графа G,
що складається з n
вершин
і m
дуг,
визначаються як:
|
якщо вершина хi – початок дуги aj; |
якщо вершина хi кінець дуги aj; |
|
якщо вершина хi не інцидентна дузі aj. |
|
|
(i=1, 2,…,n; j=1, 2,…, m). |

 Рисунок
4.1
Рисунок
4.1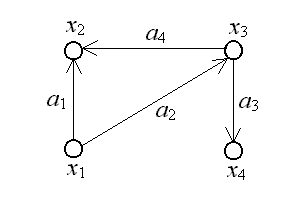 Рисунок
4.2
Рисунок
4.2
