16. Встановлення найбільш економічного об’єму партії у детермінованій моделі без дефіциту (формулою Уілсона).

. (2.10)

Формула (2.10) називається формулою Уілсона або формулою найбільш економічного об’єму партії, широко використовується в економіці. Ця формула може бути отримана і іншим способом, якщо врахувати, що добуток С₁С₂=0,5с₁с₂Nθ є величина постійна, незалежна від n. В цьому випадку, як відомо, сума двох величин приймає найменше значення, коли вони рівні, тобто С₁=С₂ або

, (2.11)

звідки отримуємо (2.9).

Із (2.11) випливає, що мінімум загальних затрат задачі управління запасами досягається тоді, коли затрати на створення запасу дорівнюють затратам на збереження запасів. При цьому мінімальні сумарні затрати

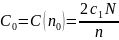, (2.12)

(Приклад 2. Потреба складального підприємства в деталях певного типу складає 120000 деталей на рік, причому ці деталі витрачаються в процесі виробництва рівномірно та безперервно. Деталі замовляються раз на рік та поставляються партіями однакового об’єму, вказаного в замовлені. Зберігання деталі на складі коштує 0,35 грошових одиниць на добу, а поставка партії – 10000 грош. одиниць. Затримка виробництва із-за відсутності деталей недопустима. Встановити найбільш економічний об’єм партії та інтервал між поставками, які необхідно вказати в замовлені (постачальник не допускає затримки поставок).

Р і ш е н н я . За умовою затрати на одну партію складають с₁=10000 грош.од., загальний проміжок часу θ=1 рік =365 днів, а загальний об’єм запасу за цей період N=120000 деталей. За формулою (2.9) , а за (2.14) .

Таким чином, найбільш економічний об’єм партії дорівнює 4335 деталей, а інтервал між поставками ≈13 днів.).

17. Статистична детермінована модель з дефіцитом.

В розглянутій моделі будемо вважати наявність дефіциту. Це означає, що при відсутності запасоємного продукту, тобто при J(t)=0 попит зберігається з тією ж інтенсивність r(t)=b, але споживання запасу відсутнє – b(t)=0, внаслідок чого накопичується дефіцит із швидкістю b. Графік зміни рівня запасу в цьому випадку представлений на рис. 2.3.

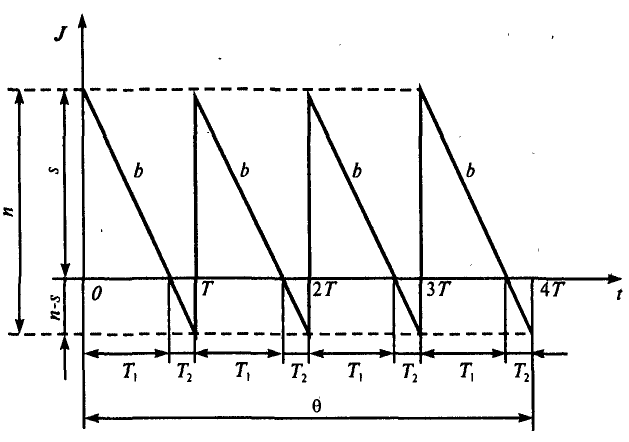
Рис.2.3.

Спадання графіку нижче осі абсцис в область від’ємних значень на відміну від графіка на рис 2.2 характеризує накопичення дефіциту.

З рис.2.3 видно, що кожний період «пилки» розбиваються на два часових інтервали, тобто , де Т₁ – час, на протязі якого відбувається споживання запасу, Т₂ – час, коли запас відсутній та накопичується дефіцит, який буде перекритий в момент надходження наступної партії.

Необхідність покриття дефіциту приводить до того, що максимальний рівень запасу s в момент надходження кожної партії тепер не дорівнює його об’єму n, а менше його на величину дефіциту n-s, накопиченого за час Т₂ (див. рис.2.3).

З геометричних міркувань легко встановити, що

(2.17)

В даній моделі в функцію сумарних затрат С поряд із затратами С₁ (на поповнення запасу) та С₂ (на зберігання запасу необхідно ввести затрати С₃ – на штраф із-за дефіциту, тобто С=С₁+С₂+С₃.

Затрати С₁, як і раніше, знаходимо за формулою (2.11). В попередньому розділі було показано, що затрати С₂ при лінійних витратах запасу дорівнюють затратам на зберігання середнього запасу, який на час споживання Т₁ дорівнює ; тому з урахуванням (2.7) та (2.5) ці затрати складають

. (2.18)

При розрахунку затрат С₃ будемо вважати, що штраф за дефіцит становить за одиницю часу с₃ на кожну одиницю продукту. Так як середній рівень дефіциту за період Т₂ дорівнює (n-s)T₂/2, то штраф за цей період Т₂ складає , а за весь період  з урахуванням (2.7) і (2.19) –

. (2.19)

Тепер, враховуючи (2.12), (2.18) та (2.19), сумарні затрати дорівнюють

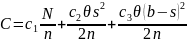. (2.20)

Неважко помітити, що при n=s формула (2.19) співпадає з отриманою раніше (2.18) в моделі без дефіциту.

18. Найбільш економічного об’єму партії у статистичній детермінованій моделі дефіцитом.

Розглянута задача управління запасами зводиться до відшукання такого об’єму партії n та максимального рівня запасу s, при яких функція С (2.16) приймає мінімальне значення. Іншими словами, необхідно дослідити функцію двох змінних C(n, s) на екстремум. Прирівнюючи часткові похідні до нуля, отримаємо після перетворення систему рівнянь:

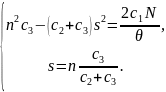(2.21)

Вирішуючи систему, отримуємо формули найбільш економічного об’єму партії та максимального рівня запасу для моделі з дефіцитом:

, (2.22)

. (2.23)

19. Поняття та розрахунок щільності збитків із-за незадоволеного попиту у статистичній детермінованій моделі дефіцитом.

Величина

(2.24)

називається щільністю збитків із-за незадоволеного попиту і відіграє важливу роль в управлінні запасами. Відмітимо, що 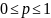. Якщо значення c₃ дорівнює з с₂, то величина p наближається до нуля: коли с₃ значно перевищує с₂, то p близька до 1. Недопустимість дефіциту рівноцінна припущенню, що або p=1.

Використовуючи (2.24), основні формули (2.22) і (2.23) можна записати компактніше:

, (2.25)

. (2.26)

Необхідно врахувати, що в силу (2.17) та (2.26) і . Тому твердження про те, що щільність збитків із-за незадоволеного попиту дорівнює p, означає , що на протязі (1-p)100% часу від повного періоду Т запас продукту буде відсутній.