12. Парамагнетизм (природа происхождения)

Парамагнетизм – вид магнетизма, проявляющийся в веществах, которые намагничиваются во внешнем магнитном поле в направлении внешнего магнитного поля. Таким образом, магнитная восприимчивость парамагнетиков имеет положительное значение, и при нормальных условиях (273.150 К, 101.325 кПа) составляет порядка 10^-5 ÷ 5·10^-3, что несколько больше (по модулю) магнитной восприимчивости нормальных диамагнетиков. Магнитная восприимчивость нормальных парамагнетиков, типичными представителями которых являются Al, Pt, щелочноземельные металлы, а также O₂, NO, MnO, FeCl₂ и др. в слабых магнитных полях не зависит от напряженности поля и существенно зависит от температуры, хотя существуют и такие парамагнетики, для которых χ от температуры зависит слабо. К последним, например, относятся щелочные металлы и металлы с аномальной температурной зависимостью, такие как Ti, Zr и другие.

Молекулы, содержащие более одного атома, как правило, имеют четное число электронов, магнитные моменты которых компенсируют друг друга, такие молекулы диамагнитны. Молекулы же с некомпенсированными магнитными моментами обычно обладают парамагнитными свойствами.

Парамагнетики обладают свойством насыщения, т. е. в очень сильных полях, или при очень низких температурах их намагниченность стремится к определенному пределу. Для намагничивания парамагнетиков до такого состояния, когда все элементарные магнитные моменты становятся параллельными внешнему полю при н. у. требуется напряженность магнитного поля ~10¹¹ А/м, а при температуре 1 K – 3·10⁵ А/м.

Как уже отмечалось, одним из необходимых условий парамагнитного состояния является наличие в атомах или молекулах некомпенсированных магнитных моментов μ_M, которые, для большей наглядности, допустимо представлять в виде элементарных магнитиков.

При отсутствии внешнего магнитного поля упорядоченному расположению этих магнитиков препятствует тепловое движение. Расчеты показывают, что энергия магнитного взаимодействия двух магнитиков составляет порядка 10^-23 Дж. А тепловая энергия, даже при 10 K равна 10^-22 Дж, что на порядок выше. Поэтому при обычных температурах магнитные моменты разупорядочены и результирующая намагниченность равна нулю

13. Законы Кюри и Кюри-Вейсса

В 1905 г., на основе методов статической физики Ланжевеном была решена задача нахождения значения намагниченности, и установлено выражение для результирующего магнитного момента N частиц:

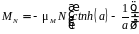(2.19)

где 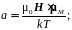k – постоянная Планка; N – количество атомов, содержащихся в объеме V с некомпенсированным магнитным моментом μ_M при температуре T.

Функцию называют функцией Ланжевена. При нормальных условиях, и не очень сильных полях (a << 1) очевидно, что энергия взаимодействия магнитного момента парамагнетиков с внешним полем мала по сравнению с энергией теплового движения.

Учитывая, что вместо (2.19) запишем:

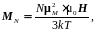(2.20)

откуда намагниченность I и объемная магнитная восприимчивость χ определяться по формулам (2.21) и (2.22) соответственно.

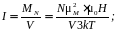(2.21)

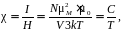(2.22)

где C – постоянная Кюри (2.23), определяемая для каждого вещества.

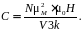(2.23)

Выражение (2.23) представляет собой закон Кюри, при доказательстве которого не учитывались силы взаимодействия между элементарными носителями магнетизма парамагнетика (молекулярное магнитное поле). Закон Кюри правдоподобно описывает температурную зависимость лишь тех парамагнитных материалов, молекулярное взаимодействие между элементарными носителями магнетизма которых мало (например, O₂, NO и др.).

Для учета влияния молекулярного магнитного поля Вейсс предложил считать это поле пропорциональным намагниченности, появившейся вследствие упорядоченности, на основании чего, в парамагнетике действует поле:

H_эфф=H+nI, (2.24)

где n – коэффициент пропорциональности.

Подставляя выражение (2.24) в (2.21), и учитывая (2.22), получим:

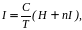(2.25)

отсюда следует, что

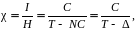(2.26)

где Δ – постоянная Вейсса.

Выражение (2.26) представляет собой более общий (по сравнению с законом Кюри) закон Кюри-Вейсса