9. Понятие «спина». Основные квантовые числа

Одновременно с развитием квантовой теории и применением ее для объяснения природы магнетизма, было сделано значительное открытие, связанное с понятием «спин» (от англ. to spin – вращаться).

Если рассмотреть модель электрона в виде тора (замкнутого на себя потока энергии), то спин представляется, как магнитный момент, возникающий в результате циркуляции по кольцу распределенного электрического заряда, суммарно равного элементарному (рис. 2.1).

В простейшем одноэлектронном случае радиус электрона совпадает с первой боровской орбитой, и связан с длиной волны соотношением Комптона:

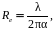
где α – постоянная тонкой структуры:

Рис. 2.1. Тороидальная модель электрона

Объясняя результаты последующих магнитомеханических экспериментов с учетом понятия спина, было установлено:

(2.13)

где m_s – спиновое магнитное квантовое число (m_s=±½)

Следовательно, отношение собственного магнитного момента электрона к собственному механическому моменту можно представить в виде (2.14):

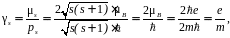(2.14)

где γ_s – собственное гиромагнитное отношение электрона; s – спиновое квантовое число (s=±½).

Далее различными методами были получены гиромагнитные (магнитомеханические) отношения для ряда элементов, в единицах e/(2m):

Железо (Fe)………………………………….….1.93;

Кобальт (Co)………………………………….....1.85;

Никель (Ni)...........................................................1.84 – 1.92;

Магнетит (Fe₃O₄).................................................1.93;

Пермаллой (сплав никеля с железом)………...1.90.

Эти данные свидетельствуют о том, что основную роль в образовании магнитных моментов для ферромагнетиков играют спиновые моменты при g_l приближающемся к 2.

Состояние движения изолированного электрона в кулоновском поле ядра атома характеризуется четырьмя квантовыми числами: n, l, m_l, m_s. Этими же числами характеризуют состояние электрона и сложных атомов, в которых имеет место взаимодействие между электронами.

Совокупность электронов, обладающих одним и тем же квантовым числом n, образует оболочку атома. Оболочки атома при n=1, 2, 3, 4, 5... обозначают соответственно буквами K, L, M, N, O, P и Q.

10. Природа атомного магнетизма

11. Диамагнетизм

Диамагнетизм – один из видов магнетизма, который проявляется в намагничивании вещества навстречу направлению, действующему на него внешнего магнитного поля.

К диамагнетикам относятся все инертные газы (He, Ne, Ar, Kr, Xe, Rn), газы (H₂, N₂, Cl₂, NH₃ и др.), ряд металлов (Zn, Cu, Au, Hg и др.), неметаллы (Si, P, S и др.), а также NaCl, SiO₂, H₂О и некоторые прочие вещества.

Качественное объяснение явления диамагнетизма состоит в следующем. Под действием внешнего поля, по закону электромагнитной индукции (1.20), в замкнутом контуре (которым в данном случае является движущийся по орбите электрон) возникает электродвижущая сила и дополнительный ток. Этот ток создает момент, противоположно направленный внешнему полю.

В общем виде, грамм-атомная диамагнитная восприимчивость χ_A определяется экспериментально, либо вычисляется по формуле Ланжевена-Паули (2.17), из которой следует, что диамагнитная восприимчивость зависит от радиусов электронных орбит и не зависит от температуры и напряженности поля. Здесь предполагается, что электрон движется по круговой орбите радиусом r, плоскость которой перпендикулярна H [5].

(2.17)

где N_A – число Авогадро; 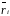– среднее значение квадрата радиуса орбиты; z – число электронов, входящих в состав атома.

Выражение (2.17) относится к диамагнетизму атомных остовов. Диамагнетизм металлов можно рассматривать как сумму диамагнетизмов атомных остовов и электронного газа. Расчеты по определению диамагнитной восприимчивости электронного газа показали, что эта восприимчивость так же не зависит от температуры, и очень мала.

Помимо рассматриваемых нормальных диамагнетиков, различают также аномальные (например, Bi) обладающие повышенной и зависящей от температуры диамагнитной восприимчивостью (на ~3 порядка выше, чем у нормальных диамагнетиков), и «сверхдиамагнетики», к которым относятся Zn, Be, Bi в сверхпроводящем состоянии (χ достигает значения ~8·10^-1).

В целом, ввиду малости диамагнитного эффекта, (у большинства диамагнетиков χ ~ 10^-6), в технике он практически не используется, хотя его исследование и представляет определенный интерес в некоторых разделах теоретической физики.