6. Уравнения Максвелла. Интегральная и дифференциальная форма записей; физический смысл; система материальных уравнений Максвелла
Система уравнений, Максвелла, сформулированная на основе законов (1.17), (1.19), (1.20), вместе с законом Лоренца (1.4) является фундаментом классической электродинамики. В настоящее время наиболее широко распространена следующая математическая формулировка данной системы:
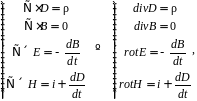(1.22)
где D – электрическая индукция, [Кл/м2]; i – плотность электрического тока, [А/м2]; ρ – плотность стороннего электрического заряда, [Кл/м3].
Физический смысл системы (1.22) заключается в следующем:
электрический заряд является источником электрической индукции;
не существует магнитных зарядов;
изменение магнитной индукции порождает вихревое электрическое поле;
электрический ток и изменение электрической индукции порождают вихревое магнитное поле.
Согласно теореме Остроградского-Гаусса (1.23), определяющей поток векторного поля через замкнутую поверхность как интеграл от дивергенции этого поля по объему, замкнутого под поверхностью, систему уравнений Максвелла можно также записать и в интегральном виде (1.24).
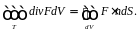(1.23)
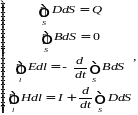(1.24)
где S – двумерная замкнутая в случае теоремы Гаусса поверхность, ограничивающая объем V, и открытая поверхность в случае закона Фарадея и Ампера-Максвелла (ее границей является замкнутый контур l); Q = ∫V ρdV – электрический заряд, заключенный в объеме V, ограниченном поверхностью S; I = ∫S idS – электрический ток, проходящий через поверхность S.
При интегрировании по замкнутой поверхности вектор элемента площади dS направлен из объема наружу. Ориентация dS при интегрировании по незамкнутой поверхности определяется направлением правого винта, «вкручивающегося» при повороте в направлении обхода контурного интервала по dl.
Изменение магнитного потока в законе Фарадея и потока электрической индукции в законе Ампера-Максвелла могут происходить как в случае зависящих от времени полей, так и в результате изменения области интегрирования (ориентации площади S или ее геометрических размеров).
Уравнения Максвелла в интегральной форме справедливы и в тех случаях, когда существуют поверхности разрыва, на которых свойства среды или напряженности электрического или магнитного поля меняются скачкообразно. Таким образом, интегральная форма записи уравнений Максвелла обладает большей общностью, чем дифференциальная, предполагающая, что все величины в пространстве и во времени меняются непрерывно. Система (1.24) позволяет интерпретировать постулаты Максвелла несколько иначе:
поток электрической индукции через замкнутую поверхность S пропорционален величине свободного заряда находящегося в объемe V, который окружает поверхность S;
поток магнитной индукции через замкнутую поверхность равен нулю;
изменение потока магнитной индукции, проходящего через незамкнутую поверхность S, взятое с обратным знаком, пропорционально циркуляции электрического поля на замкнутом контуре l, который является границей поверхности S;
полный электрический ток свободных зарядов и изменение потока электрической индукции через незамкнутую поверхность S, пропорциональны циркуляции магнитного поля на замкнутом контуре l, который является границей поверхности S.
Очевидно, что система уравнений (1.24) не составляет полного описания электромагнитного поля, поскольку не содержит свойств среды, в которой оно возбуждено. Соотношения, учитывающие индивидуальные свойства среды, известны как система материальных уравнений Максвелла.
В изотропных и однородных средах материальные уравнения Максвелла принимают вид системы (1.25).
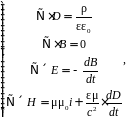(1.25)
где ρ – плотность электрического заряда; ε – относительная диэлектрическая проницаемость среды; ε0 – электрическая постоянная; i – плотность тока; μ – относительная магнитная проницаемость среды; μ0 – магнитная постоянная.
В оптическом диапазоне частот электромагнитных волн, вместо понятия диэлектрической проницаемости ε обычно применяют термин «показатель преломления» определяемый как n2=εμ (зависящий от длины волны), и показывающий отличия скорости распространения монохроматической световой волны в среде от скорости света в вакууме. При этом в оптическом диапазоне диэлектрическая проницаемость заметно меньше чем на низких частотах, а магнитная проницаемость большинства оптических сред практически равна единице. В вакууме диэлектрическая и магнитная проницаемости равны единице