4.Формы записи и физический смысл законов Био-Савара-Лапласса, Гаусса
Еще один закон, сформулированный в результате эмпирических исследований, определяет магнитное поле движущегося точечного заряда q и математически дается выражением (1.10).
(1.10)
где r – радиус-вектор, проведенный от заряда q к точке наблюдения. Напряженность электрического поля неподвижного заряда, той же величины q, в той же точке наблюдения задается выражением (1.11).
(1.11)
Учитывая (1.11), выражение (1.10) можно записать в виде:
(1.12)
причем (v << c), где c – скорость распространения электромагнитного поля в вакууме (скорость света).
Далее рассмотрим закон, определяющий магнитное поле отдельного элемента тока. Согласно принципу суперпозиции, магнитные поля отдельных движущихся зарядов векторно складываются, причем каждый заряд возбуждает поле, абсолютно не зависящее от наличия других зарядов. Согласно выражению (1.10) принцип суперпозиции приводит к следующему выражению магнитного поля объемного элемента тока:
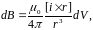(1.13)
и аналогично для линейного элемента тока:
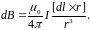(1.14)
Выражения (1.13) и (1.14) представляют собой так называемый закон Био-Савара-Лапласа.
Полное поле находится интегрированием выражений (1.13) и (1.14) по всем токам: [2]
(1.15)
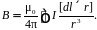(1.16)
Здесь следует отметить, что выражения (1.13) – (1.16) справедливы лишь для постоянных токов, а так как постоянные токи всегда замкнуты, то выражения (1.13) и (1.14) подтвердить опытным путем принципиально недоступно.
Предполагая, что магнитное поле возбуждается равномерно движущимися точечными зарядами, ФB – поток вектора B через замкнутую поверхность, а так же циркуляция того же вектора по замкнутому контуру будет определяться согласно теореме Гаусса для магнитного поля (1.17).
(1.17)
Другими словами, поток магнитного поля через любую замкнутую поверхность равен нулю, откуда следует, что магнитного заряда не существует, а само магнитное поле имеет вихревой характер.
Так как условие (1.17) выполняется для любых подобластей некоторой области W, то оно равносильно тому, что равна нулю дивергенция векторного поля B:
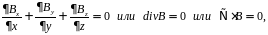(1.18)
где
– оператор набла, определяемый как
.
Такая особенность распространения магнитного поля является принципиально отличной от свойств распространения поля электрического, описываемого законом Гаусса (1.19), согласно которому поток вектора электрической индукции через замкнутую поверхность пропорционален заключенному внутри этой поверхности свободному электрическому заряду.
(1.19)
где Q – полный заряд, содержащийся в объеме, ограничивающем поверхность S.
5. Закон электромагнитной индукции
Несколько позже, в 1831 г. Фарадеем было экспериментально установлено явление электромагнитной индукции – возникновение электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через данный контур. Математически, закон электромагнитной индукции дается как: [2]
(1.20)
где ℰ – ЭДС, действующая вдоль произвольно выбранного контура.
Знак «-» в выражении (1.20) объясняется тем, что индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.
Закон Фарадея (закон электромагнитной индукции), записанный в дифференциальной форме, имеет вид:
