28. Эффект Гаусса

• Эффект Гаусса – эффект зависимости удельного сопротивления полупроводника (металла), помещенного в магнитное поле, от значения индукции этого поля.

Такая зависимость объясняется тем, что носители заряда (фермионы), перемещающиеся в полупроводнике (металле) под действием электрического поля, обладают не одинаковыми значениями скорости перемещения, так как известно, что скорости носителей заряда подчиняются распределению, отвечающему статистике Ферми-Дирака:

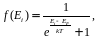
где E_F – энергия Ферми; E_i – энергия i-го состояния фермиона; k – постоянная Больцмана; T – абсолютная температура.

В результате, наводимое поперечное поле Холла (4.1) компенсирует влияние силы Лоренца только на носители тока, имеющие некоторую скорость v (рис. 4.1). Траектория же носителей тока, скорость которых отлична от v, будет искривляться, приобретая дугообразную форму (рис. 1.1).

Такое искривление траекторий движения заряженных частиц приводит к увеличению числа их столкновений (сокращению длины свободного пробега), а, следовательно, – к понижению значения удельной проводимости и увеличению удельного сопротивления проводника или полупроводника (так называемый «физический эффект магнитосопротивления»).

Оценку приращения удельного сопротивления в полупроводнике n-типа или металле, для случая слабых магнитных полей (μB << 1), можно произвести в соответствии с выражением 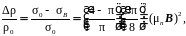(4.6).

(4.6)

где Δρ – приращение удельного сопротивления; ρ₀ – удельное сопротивление материала вне магнитного поля; σ₀ – удельная электрическая проводимость материала вне магнитного поля; σ_B – удельная электрическая проводимость в магнитном поле с индукцией B; μ_n – подвижность носителей заряда [12].

Естественно, что понятия слабого и сильного магнитных полей относительны, поскольку в условия μB << 1 и μB >> 1 кроме магнитной индукции B, входит значение подвижности носителей заряда μ. Таким образом, сильное для полупроводников с высокой подвижностью электронов магнитное поле может являться слабым для полупроводников с меньшей подвижностью.

В случае участия в проводимости носителей заряда обоих знаков выражение (4.6) принимает следующий вид:

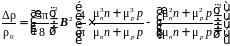(4.7)

где μ_n и μ_p – подвижности электронов и дырок соответственно; n и p – концентрация электронов и дырок соответственно.

Наибольшее возможное значение величины ∆ρ/ρ₀ в полупроводнике (зная зависимости μ_n и μ_p от концентрации) можно определить из выражения 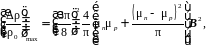(4.8).

(4.8)

при этом отношение концентраций носителей заряда должно удовлетворять условию:

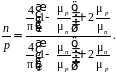
Таким образом, как следует из выражений (4.7) и (4.8), приращение сопротивления в области малых магнитных полей пропорционально квадратам подвижности носителей тока и магнитной индукции.

В связи с некоторой громоздкостью выражений (4.6) – (4.8) для приблизительного описания эффекта магнитосопротивления в большом диапазоне значений магнитной индукции, предлагается применять более лаконичное и удобное для проведения расчетов, выражение 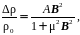(4.9).

(4.9)

где A – коэффициент формы магниторезистора, при условии выражения подвижности носителей в единицах [см²·В^-1·см^-1], принимающий значение порядка ~10^-12.

Из выражения (4.9) следует, что при малых значениях магнитной индукции, величина ∆ρ/ρ₀ квадратично зависит от B, тогда как при больших значениях B отношение ∆ρ/ρ₀ достигает насыщения.

В инженерной практике для оценки относительного изменения сопротивления полупроводника в магнитном поле также часто используется следующее выражение:

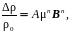(4.10)

где n – показатель степени, принимающий значения от 1 до 2, в зависимости от величины магнитной индукции.