27. Эффект Холла

• Эффект Холла – явление возникновения поперечной разности потенциалов при помещении металла (полупроводника), вдоль которого течет постоянный электрический ток, в поперечное току магнитное поле.

В случае проводника (полупроводника), помещенного в магнитное поле, как показано на рис. 4.1, составляющие электрического поля и напряжения будут определяться в соответствии с системой (4.1) и (4.2) соответственно.

(4.1)

где E_x, E_y, E_z – электрическое поле вдоль осей X, Y, Z соответственно; tan (θ_n)=-μ_nB_z; μ_n – подвижность носителей заряда; B_z – индукция внешнего магнитного поля, направленного вдоль оси Z; θ_n – угол Холла; ρ_n – удельное сопротивление материала; i_x = I_x/(bc); b и c – ширина и толщина материала соответственно; I_x – ток, протекающий в образце вдоль оси X.

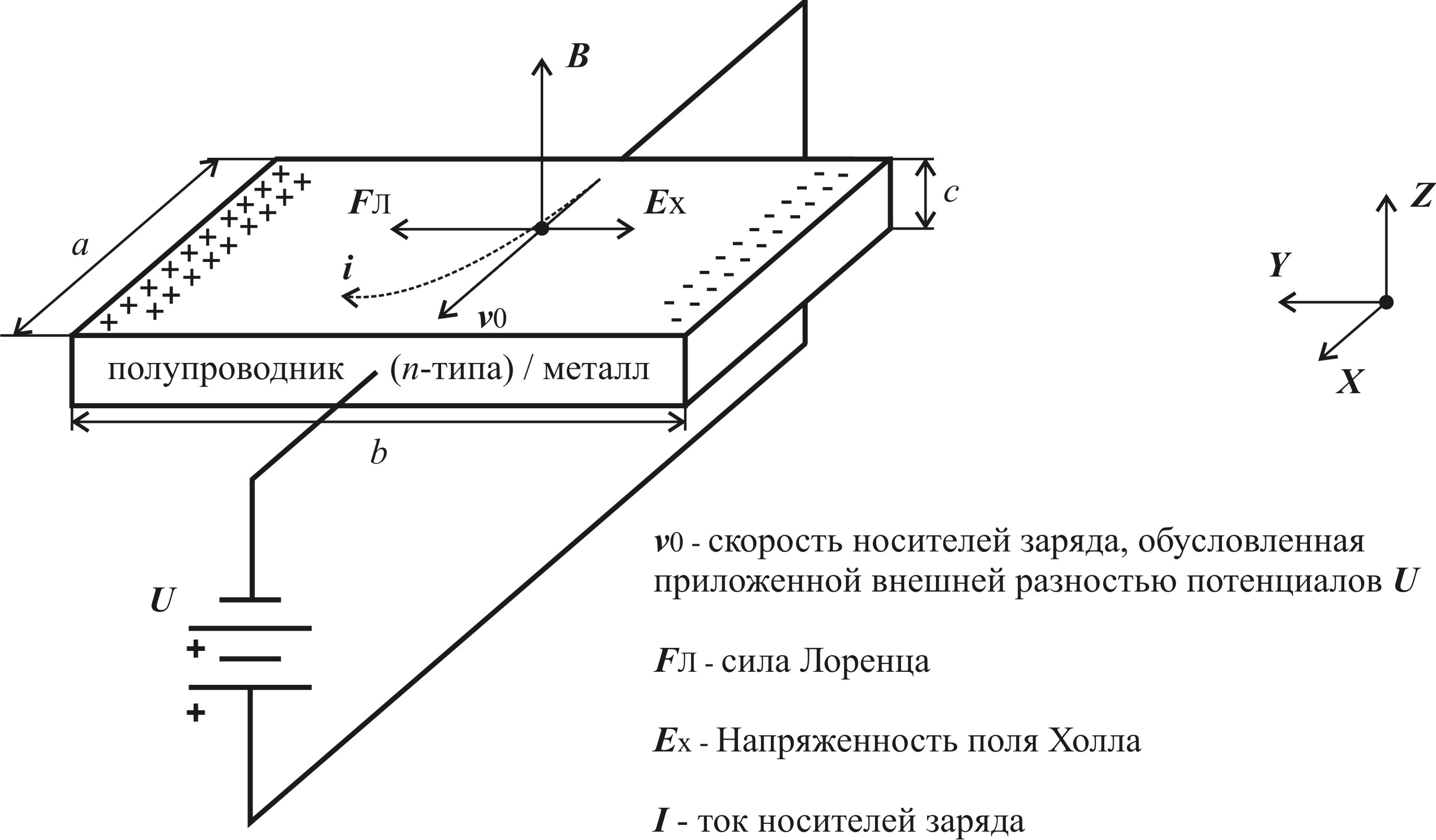
Рис. 4.1. Эффект Холла в полупроводниковой (металлической) пластине

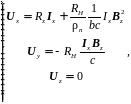(4.2)

где R_x – сопротивление полупроводника вдоль оси X; R_H – постоянная Холла.

Напряжение U_x складывается из омического падения напряжения на пластине и напряжения, возникающего в результате так называемого продольного эффекта Холла, причем, это последнее слагаемое, обычно мало по сравнению со слогаемым I_xR_x.

Если рассматривать случай, когда угол между I и B не является прямым, составляющая U_z ≠ 0 (планарный эффект Холла):

(4.3)

где ψ – угол между I и B.

Постоянная Холла в выражениях (4.2) и (4.3) определяется по формуле (4.4), где в случае металлов или вырожденного полупроводника A=1. При определении R_H полупроводникa p- или n-типа следует также учитывать влияние рассеяния носителей тока. В этом случае коэффициент A будет зависеть от механизма рассеяния носителей тока в монокристаллической решетке: в случаях рассеяния на тепловых колебаниях решетки A=3π/8; в случае рассеяния на ионизированных примесях A=1.93.

(4.4)

где q – заряд носителей тока, n – концентрация носителей заряда.

Выражение (4.4) справедливо лишь для проводников с единственным типом носителей тока (только электроны или только дырки). В случае проводника со смешанным типом проводимости (полупроводник i-типа), то есть когда подвижность электронов и дырок сопоставимы между собой, выражение для коэффициента Холла принимает вид:

(4.5)

где μ_n, μ_p – подвижность электронов и дырок соответственно; n и p – концентрация электронов и дырок соответственно.

Касательно понятия подвижности носителей заряда, здесь следует пояснить, что движение свободных носителей заряда в кристалле полупроводника рассматривается как движение в вакууме свободных электронов, обладающих эффективной массой m^*. При создании вдоль проводящего тела электрического поля Е, все электроны передвигаются вдоль силовых линий этого поля с некоторой средней скоростью v_ср. Отношение этой скорости к напряженности электрического поля в веществе называется подвижностью носителей тока или заряда:

где E – напряженность электрического поля; – среднее время свободного пробега носителей тока.