16. Петли гистерезиса( классификация, основные характеристики)
Основная кривая намагничивания является важнейшей характеристикой магнитных материалов, и широко используется для оценки их намагничивания в постоянных полях.
На основной кривой намагничивания принято различать три участка: начальный, соответствующий нижнему колену кривой, участок быстрого возрастания индукции (намагниченности) и участок насыщения (выше верхнего колена кривой).
При циклическом перемагничивании кривая намагничивания образует петлю гистерезиса, как показано на рис. 2.5 (некоторые материалы обладают более сложной формой петли гистерезиса).
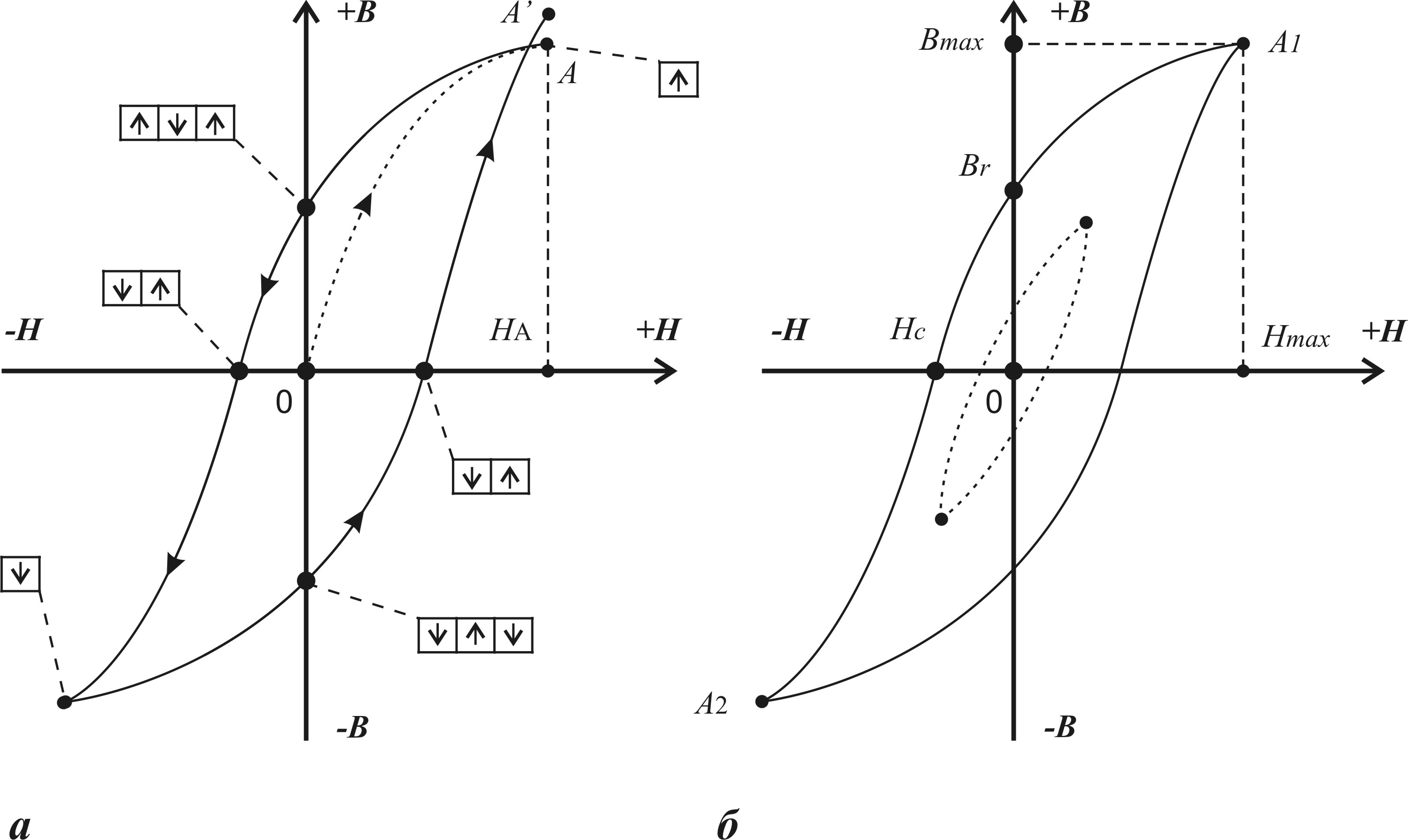
Рис. 2.5. Петли гистерезиса
Если намагничивание происходит так, как показано стрелками на рис. 2.5, а, то при однократном прохождении петли точки A и A’, соответствующие одному и тому же полю H не совпадают, что объясняется различной для этих точек магнитной историей.
Для получения более определенной симметричной (установившейся) петли (рис. 2.5, б) при измерении в цепях постоянного тока производят так называемую магнитную подготовку, которая заключается в многократном (5–10 раз) коммутировании тока в намагничивающей обмотке после установления его значения.
Форма петли для данного материала зависит от значения поля Hmax. Для слабых полей она имеет вид эллипсов, с увеличением поля у нее начинают вытягиваться «носики», соответствующие точкам A1 и A2 (рис. 2.5, б).
Петли гистерезиса, полученные при условии насыщения, называют предельными, именно они обычно и приводятся в специализированных справочниках.
Основными характеристиками петли гистерезиса является:
остаточная индукция Br – индукция, которая остается в предварительно намагниченном образце после снятия внешнего магнитного поля;
коэрцитивная сила Hс – размагничивающее поле, которое должно быть приложено к предварительно намагниченному образцу, для того, чтобы индукция в нем стала равной нулю;
потери на гистерезис Pг (площадь петли гистерезиса одного цикла перемагничивания), отнесенные к единице объема вещества (удельные потери), определяемые по формуле (2.28).
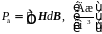(2.28)
При перемагничивании материала с частотой f потери на гистерезис будут определяться согласно выражению (2.29).
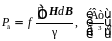(2.29)
где γ – плотность вещества, кг/м3.
Так же здесь следует различать абсолютную и относительную магнитные проницаемости, задаваемые формулами (2.30) и (2.31) соответственно.
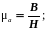(2.30)
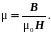(2.31)
17. Свойства магнитных материалов, используемых в цепях переменного тока
Так, наиболее часто используются понятия нормальной магнитной проницаемости μ (слово «нормальная» обычно опускается), начальной магнитной проницаемости μнач, а так же максимальной μmax, импульсной μи и дифференциальной μдиф.
Для точки A (рис. 2.6) магнитная проницаемость μ определяется как тангенс угла наклона секущей OA к оси абсцисс, т. е.
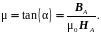(2.32)
Начальная и максимальная проницаемости представляют собой частные случаи нормальной проницаемости:
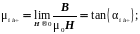(2.33)
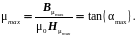(2.34)
Таким образом, наклон касательной на начальном участке кривой B = f(H), характеризует начальную проницаемость, а наклон прямой, проведенной из начала координат в точку верхнего перегиба кривой, соответствует максимальной проницаемости.
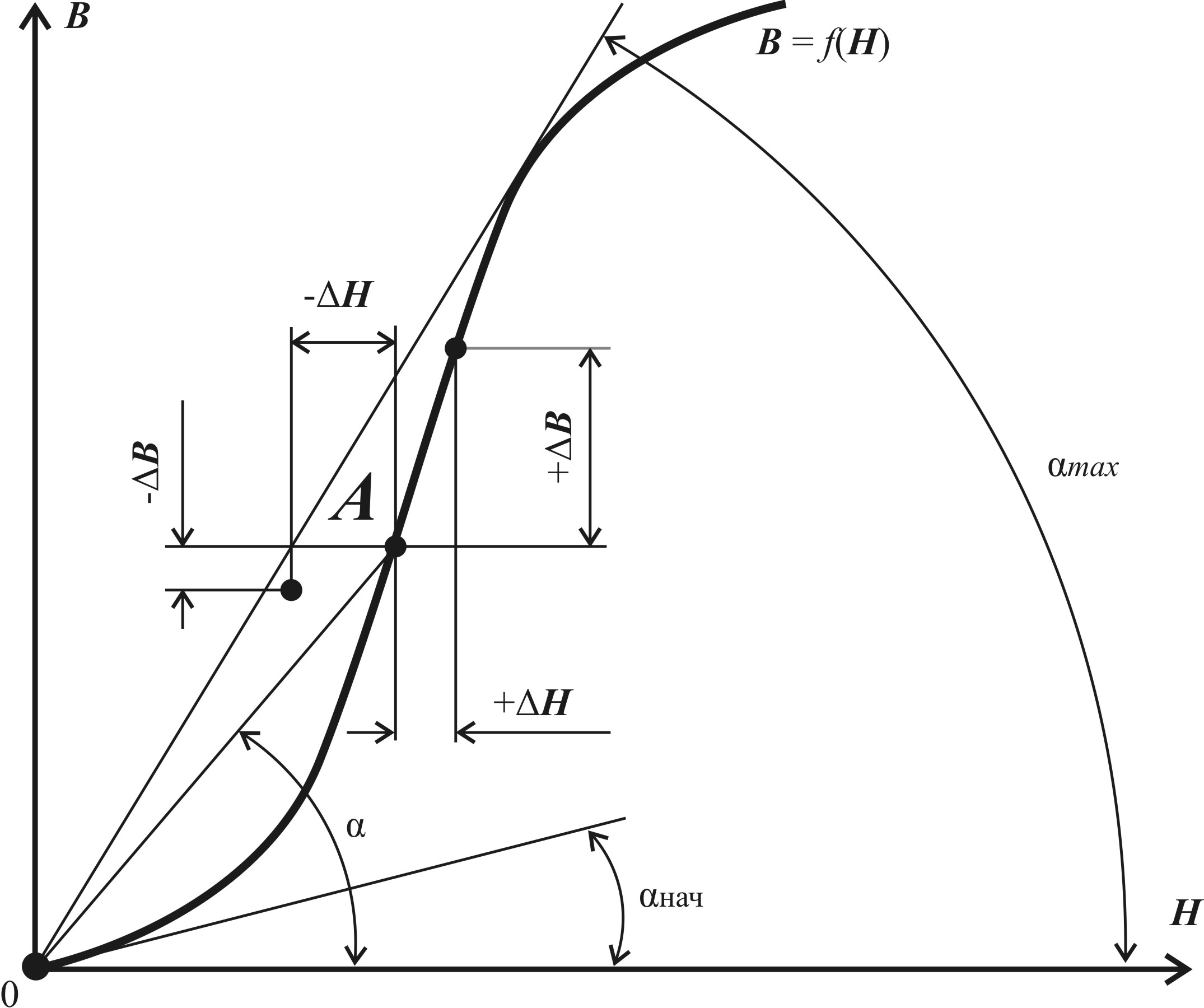
Рис. 2.6. К объяснению понятий различных магнитных проницаемостей
Дифференциальную проницаемость определяют, как производную магнитной индукции по напряженности магнитного поля для любой точки кривой намагничивания, т. е. она представляет собой тангенс угла между осью абсцисс и касательной к кривой намагничивания в этой точке.
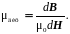(2.35)
Понятие μдиф чаще всего используют при анализе вопросов, связанных с одновременным действием на магнитный материал постоянного H0 и переменного H~ магнитных полей, причем H~<< |H0|.
Импульсная магнитная проницаемость определяется как:
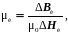(2.36)
где ΔBи – максимальное изменение магнитной индукции при намагничивании импульсным полем ΔHи.
При намагничивании магнитного материала переменным полем петля гистерезиса, характеризующая затраты энергии в течение одного цикла перемагничивания расширяется (увеличивает свою площадь), как за счет потерь на гистерезис Pг, так и за счет потерь на вихревые токи Pв и дополнительные потери Pд. Такую петлю называют динамической, а сумму составляющих потерь – полными или суммарными потерями.
Удельные потери на гистерезис при частоте перемагничивания f определяются согласно выражению (2.28). Потери же на вихревые токи зависят не только от магнитных, но и от электрических свойств материала (удельного электрического сопротивления). Для листового образца удельные потери на вихревые токи находят по формуле (2.37).
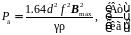(2.37)
где Bmax – амплитуда магнитной индукции; f – частота переменного тока; d – толщина листа; γ – плотность материала; ρ – удельное электрическое сопротивление материала.
Дополнительные потери нельзя рассчитать аналитически, их определяют как разность между полными потерями и суммой потерь на гистерезис и вихревые токи:
Pд = P-(Pг + Pв). (2.38)
В соответствии с определением основной кривой намагничивания, геометрическое место вершин динамических петель называют динамической кривой намагничивания, а отношение индукции к напряженности поля на этой кривой – динамической магнитной проницаемостью μ~.
При изменении во времени величин B и H необходимо учитывать два явления: искажение формы кривой и сдвиг по фазе между магнитной индукцией и напряженностью магнитного поля.
Зависимость между B и H определяется формой динамической петли, поэтому, при синусоидальном изменении одной из рассматриваемых величин в общем случае, вторая – изменяется не синусоидально (появляются высшие гармоники). Одновременное синусоидальное изменение B и H возможно лишь в случае эллиптической петли.
При заданном значении Bmax форма и площадь динамической петли зависят от того, что именно изменяется по синусоидальному закону – магнитная индукция или напряженность поля.
При синусоидальной индукции петля более узкая (потери меньше), чем при синусоидальной напряженности поля. Это объясняется тем, что согласно (2.37) потери на вихревые токи возрастают очень быстро при наличии высших гармонических составляющих на кривой магнитной индукции. Чем большее сопротивление включено последовательно с намагничивающей обмоткой магнитного элемента, тем ближе к синусоидальной форма кривой напряженности магнитного поля, и наоборот.
Что же касается отставания по фазе кривой индукции от кривой напряженности поля, то это явление объясняется действием вихревых токов, препятствующих (согласно закону Ленца) изменению индукции, гистерезисом и магнитной вязкостью. Угол отставания δ в данном случае называют углом потерь.
С целью математического учета искажений формы кривой и сдвига по фазе в зависимости B = f(H) при намагничивании переменным полем В предлагается заменить реальную динамическую петлю эквивалентным эллипсом, уравнения которого в координатах h и b имеют вид выражений (2.39) и (2.40) соответственно.
h = Hmaxsin(ωt); (2.39)
b = Bmaxsin(ωt-δ). (2.40)
Введение эквивалентного эллипса не только позволяет решить сложную задачу, но и во многих случаях приблизиться к реальным условиям намагничивания, так как в слабых полях и на высоких частотах динамическая петля практически является эллипсоидом. Если ввести составляющую индукции Bmax1=Bmax·cos(δ), совпадающую по фазе с напряженностью H, и составляющую Bmax2=Bmax·sin(δ), отстающую на 90° от напряженности H, то можно показать, что Bmax1 связана с обратимыми процессами превращения энергии при перемагничивании, Bmax2 – с необратимыми.
Помимо параметров Hmax, Bmax, Bmax1, Bmax2 и угла потерь δ, для характеристики магнитных свойств материалов, используемых в цепях переменного тока, применяются следующие виды магнитной проницаемости:
амплитудная (полная) проницаемость
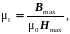(2.41)
где μп не определяет фазового сдвига и должна быть дополнена другими понятиями;
упругая проницаемость
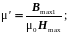(2.42)
вязкая проницаемость
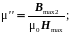(2.43)
комплексная проницаемость
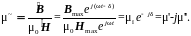(2.44)
Очевидно, что последний вид проницаемости описывает процессы намагничивания в переменных полях наиболее полно.
При магнитных измерениях в переменных полях чаще всего применяют зависимости Bmax = f(Hmax) с одновременным измерением угла потерь δ. Пользуются и другими зависимостями, например Bmax1 = f(Hmax1), где Bmax1 и Hmax1 – амплитудные значения переменных гармоник.