2. Предел числовой последовательности. Свойства сходящихся последовательностей.

О п р е д е л е н и е 1 Число называется пределом число- вой последовательности при , если для любого числа существует номер , начиная с которого все элементы последовательности удовлетворяют неравенству

. (3)

Символически это записывается так , или при .

Если последовательность имеет предел, то её называют сходящейся; ели же предела не существует, то её называют расходящейся.

Замечание 1 В соответствии с этим определением, всякая бесконечно малая последовательность имеет предел и этот предел равен нулю.

Замечание 2 Бесконечно большие последовательности иногда называют последовательностями, сходящимися к бесконечности и записывают .

Замечание 3. Если , то последовательность является бесконечно малой. Следовательно, любой элемент сходящейся последовательность можно представить в виде

, (4)

где - элемент бесконечно малой последовательности.

Замечание 4. Неравенство (3) равносильно неравенствам или . Последнее неравен -ство означает, что элементы находятся в - окрестности точки . В соответствии с этим получаем ещё одно опреде -ление сходящейся последовательности:

О п р е д е л е н и е 2. Последовательность называется сходящейся, если существует число такое, что в любой - окрестности этого числа находятся все элементы последова -тельности , начиная с некоторого номера.

Рассмотрим примеры сходящихся последовательностей.

1. Последовательность сходится и предел этой последовательности равен 1. В самом деле, разность и для доказательства сходимости достаточно убедиться, что последовательность является бесконечно малой. Для произ -вольного 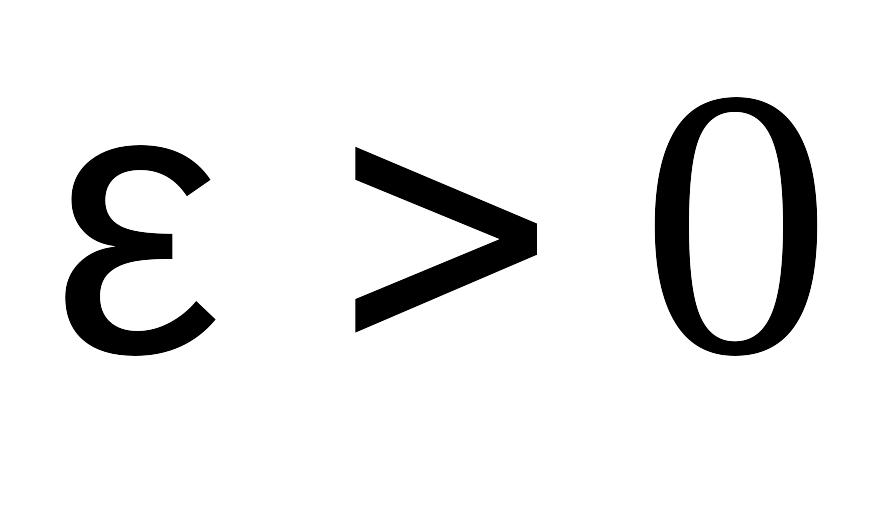можем взять любой номер . Тогда . Следовательно, для всех чисел , удовлетворяющих неравенству , будет выполнено , т.е. последова- тельность в самом деле бесконечно малая.

2. Последовательность сходится и имеет пределом число . В самом деле

. Из этих неравенств получается . Так как при , , то для произвольно взятого , выбрав номер из условия , получим при .

Основные свойства сходящихся последовательностей:

1. Сходящаяся последовательность имеет только один предел.

2. Сходящаяся последовательность ограничена.

3. Алгебраическая сумма сходящихся последовательностей является сходящейся последовательностью, причём, если , то .

4. Произведение сходящихся последовательностей является сходящейся последовательностью, причём, если , то .

5. Частное двух сходящихся последовательностей и

, при условии, что предел не равен нулю,

является сходящейся последовательностью, предел

которой равен частному пределов последовательностей

и

6. Из сходимости последовательности следует

сходимость последовательностей

для любых чисел и .

7. Если все элементы некоторой сходящейся последовательности , начиная с некоторого номера, удовлетворяют неравенству , то и предел этой последовательности - удовлетворяет такому же неравенству, т.е. .

8. Если элементы сходящихся последовательностей

и , начиная с некоторого номера, удовлетво-

ряют неравенству , то их пределы удовлетворя-

ют тому же неравенству, т.е. .

7. Если все элементы сходящейся последовательности находятся в отрезке , то её предел также находится в этом отрезке.

8. Пусть и - сходящиеся последовательности, причём . Пусть, кроме этого, начи- ная с некоторого номера, элементы последовательнос- ти удовлетворяют неравенству: . Тогда последовательность также сходится и имеет предел, равный .

Замечание В соответствии с теоремой 1 из 1.3, любая

последовательность вида , является бесконечно малой, т.е. . Поэтому, учитывая свойства 3 – 7 сходящихся последовательностей, можем легко вычислять следующие пределы:

Пример 1. Найти предел . Разделим чис- тель и знаменатель дроби на . В результате получим

В дальнейшем, при вычислении пределов такого вида, ни к чему повторять такую последовательность операций. Легко проверить и следует запомнить следующее правило:

ПРАВИЛО: Если в дроби старшая степень числителя меньше старшей степени знаменателя, то предел равен нулю; если старшая степень числителя больше старшей степени знаменателя, то предел равен бесконечности; если старшие степени числителя и знаменателя совпадают, то предел равен отношению коэффициентов перед старшими степенями.

Рассмотрим ещё один пример:

Пример 2. Вычислить предел

.

Под знаком предела находится неопределённое выражение вида . Для вычисления такого предела желательно сначала получить дробь и затем использовать правило. Для этого умножим и разделим это выражение на сумму корней, чтобы получить в числителе разность квадратов. Получим: