8. Логарифмическое дифференцирование.

По правилу вычисления производной сложной функции, . Эта формула позволяет вычислять производные довольно сложного вида. В первую очередь к ним относятся, так называемые показательно – степенные функции вида

, где и - некоторые функции от ( ), имеющие производные в точке .

Прологарифмируем эту функцию :

.

Вычислим производную: . Отсюда, учитывая, что , получим

.

ПРИМЕР. Вычислить производную функции

Прологарифмируем это выражение:

.

Вычислим производную

,

тогда ,

или .

Учитывая свойства логарифмов (логарифм произведения равен сумме логарифмов, логарифм частного равен разности логарифмов, степень можно выносить за знак логарифма) этот же метод удобно использовать в случае, если функция задана только степенями, корнями, произведениями и дробями.

ПРИМЕР. Найти производную функции

.

Прологарифмируем эту функцию и используем свойства логарифма:

.

Тогда

.

Окончательно,

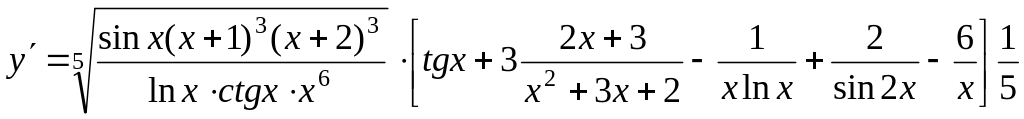Если бы мы попытались найти производную этой функции, непосредственно используя правила дифференцирования, получить результат было бы намного сложнее.

8. Производные высших порядков.

Как уже отмечалось, производная функции сама является функцией от . Следовательно, по отношению к ней, снова можно поставить вопрос о существовании произ –водной.

Назовём производной первого порядка от функции . Производная от производной некоторой функции называется производной второго порядка (или второй про- изводной) этой функции. Производная от второй производной называется производной третьего порядка (или третьей про- изводной) и т.д. Производные, начиная со второй, называются производными высших порядков и обозначаются

Рассмотрим несколько примеров

1. Найти 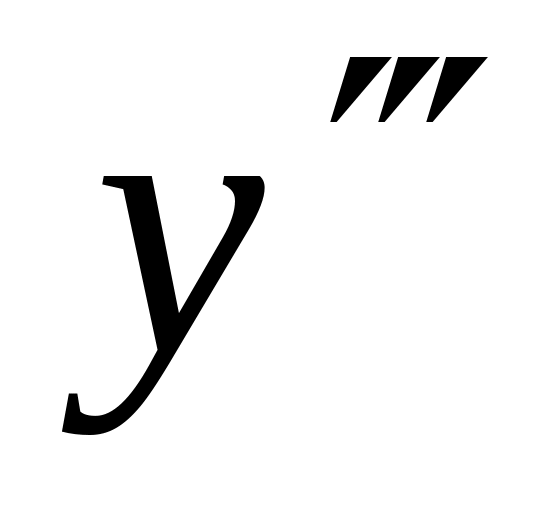для функции .

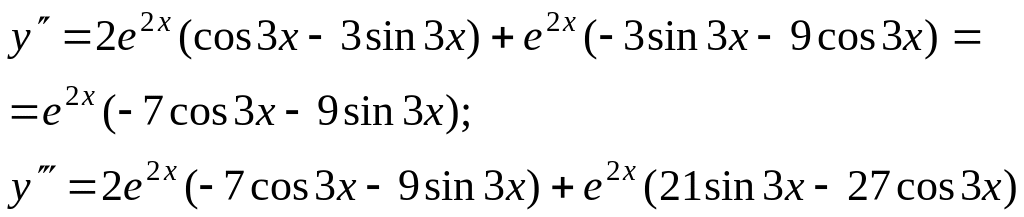
Следовательно, .

2.. Пусть . Найти производную .

3. Пусть . Тогда .

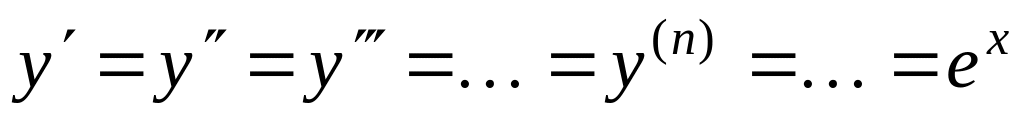5.10. Параметрически заданная функция и её

дифференцирование

Пусть даны две функции одной независимой переменной

(1)

определённые и непрерывные в одном и том же промежутке. Если строго монотонна ( если то ), то обратная к ней функция одно -значна и также строго монотонна. Поэтому можно рас -сматривать как функцию, зависящую от переменной посредством переменной , называемой параметром:

.

В этом случае говорят, что функция от задана параметрически с помощью уравнений (1).

Пример:

Пусть . Функция убывает на этом промежутке. Тогда данные уравнения задают параметрически заданную функция от .Тогда . Так как , то это уравнение определяет верхнюю половину окружности: .

Предположим теперь, что функции и имеют производные, причём . Тогда производная , или просто, .

Например. Найти производную для функции

Тогда .

Пусть теперь существуют вторые производные . Так как первую производную также является параметрически заданной функцией от , т.е.

то её производную вычисляем по той же формуле

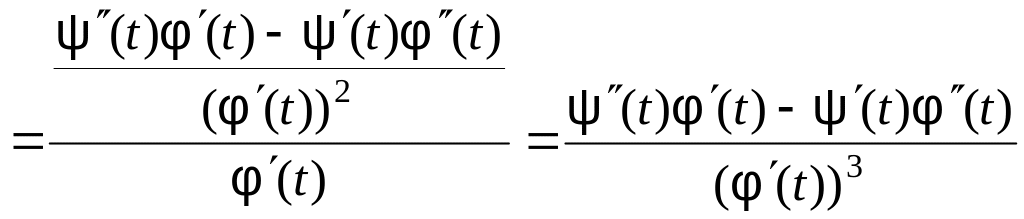. (2)

Например, пусть . Найти Тогда

Следовательно, по формуле (2)

Аналогичным образом можно вычислить производную любого порядка от функции, заданной параметрически.