МИНЕСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Московский Государственный Институт Электроники и Математики

(Технический Университет)

Курсовая работа

По курсу «Математические методы и модели исследования операций»

Задание № 28

Выполнила:

студентка группы МЭ-62

Наумова А.А.

Москва 2009 г.

Оглавление

Часть 1 2

Содержательная постановка задачи 2

Математическая постановка задачи 3

Вывод двойственной задачи 4

Нахождение оптимального решения прямой и двойственной задачи в Excel 6

Прямая задача 6

Двойственная задача 7

Анализ полученных решений 8

Отчеты для прямой задачи 8

Пример 1: «Определение нормированной стоимости и пример, показывающий ее смысл». 10

Пример 2: «Объяснить, что означают столбцы «Допустимое увеличение и «Допустимое уменьшение», привести пример изменения параметров в допустимых и вне допустимых пределов». 13

Пример 3: «Объяснить значение теневой цены и привести пример». 14

Пример 4: «Объяснить, что означают столбцы «Допустимое увеличение и «Допустимое уменьшение» для ограничений, привести пример изменения параметров допустимых и вне допустимых пределов. 16

Пример 5: «Объяснить столбцы «Нижний предел», «верхний предел», «Целевой результат». 20

Отчеты для двойственной задачи 20

Часть 1 Содержательная постановка задачи

В аптеке продается 7 наименований поливитаминов. Каждое наименование содержит витамины трех различных типов. Цены на витамины различны. Необходимо пройти профилактический курс, в течение которого с минимальными суммарными затратами получить 100 единиц витамина А, 80 единиц витамина С и 120 единиц витамина В₆. Необходимое количество поливитаминов покупается одновременно.

витамины	Содержание витаминов, ед\г							всего
	Р1	Р2	Р3	Р4	Р5	Р6	Р7	необходимо
А	5	0	2	0	3	1	2	100
С	3	1	5	0	2	0	1	80
В6	1	0	3	1	2	0	6	120
цена за г	4	1	5	6	3.5	7	4

1. Какое общее поливитаминов следует принять (г) ?

2. Какое количество поливитамина Р₁ следует принять (г)?

3. Каковы минимальные затраты на профилактический курс?

Математическая постановка задачи

Составим математическую модель. В задаче: i=(имеется 3

витамина: А,С, В₆) и j=( имеется 7 поливитаминов)

Обозначим:

-количество витамина i в j -ом поливитамине

-потребность в i-ом витамине

-цена j-ого поливитамина

-количество закупаемого j-ого поливитамина

.

Тогда расходы от покупки этих поливитаминов равен 4х₁+х₂+5х₃+6х₄+3.5х₅+7х₆+4х₇. Их нужно минимизировать. Потребление витаминов ограничено необходимым количеством.

Для А: 5х₁+2х₃+3х₅+х₆+2х₇≥ 100

Для С: 3х₁+х₂+5х₃+2х₅+х₇≥ 80

Для В₆: х₁+3х₃+х₄+2х₅+6х₇ ≥120

Еще нужно добавить ограничения х₁≥0; х₂≥0; х₃≥0;х₄≥0;х₅≥0;х₆≥0;х₇≥0.(из экономического смысла)

Таким образом, получаем задачу

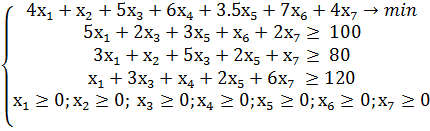
Задача линейного программирования

Вывод двойственной задачи

Воспользуемся общими правилами построения двойственной задачи:

1. Каждому ограничению ЗЛП, кроме условия не отрицательности, сопоставляется двойственная переменная.

В прямой задаче 3 ограниченияв двойственной задаче будут 3 переменных λ₁, λ₂, λ₃

Каждой переменной в исходной задаче соответствует

ограничение в двойственной задаче.

В прямой задаче 7 переменных в двойственной задаче будет 7 ограничений.

2. Ограничению неравенством исходной задачи, кроме условия не отрицательности, соответствует не отрицательная двойственная переменная. Ограничению равенством - свободная переменная.

В прямой задаче 3 ограниченияв двойственной условие не отрицательности будет состоять и 3-ех не отрицательных переменных

λ₁≥0, λ₂≥ 0,λ₃≥0

3. Если переменная исходной задачи не отрицательна, то в двойственной задаче ей соответствует ограничение неравенство. Свободной переменной, т. е. тем, на которые не наложены условия не отрицательности, соответствует ограничение равенство.

В прямой задаче 7 не отрицательных переменных в двойственной задаче будет 7 ограничений-неравенств.

4. Матрица коэффициентов ограничений двойственной задачи получается из матрицы коэффициентов прямой задачи транспонированием. И наоборот.

А = Матрица коэффициентов прямой ЗЛП

А^т = Матрица коэффициентов двойственной ЗЛП

5. Коэффициенты целевой функции исходной задачи образуют правую часть ограничений двойственной задачи. Правая часть ограничений исходной задачи является коэффициентами целевой функции в двойственной задаче.

с = (4 1 5 6 3.5 7 4) -коэффициенты целевой функции прямой ЗЛП

b = (100 80 120) - правая часть ограничений прямой ЗЛП

6. Если исходная задача - это задача на min, то двойственная задача к ней - это задача на max.

Таким образом, получили двойственную задачу:

Двойственная задача к (ЗЛП)

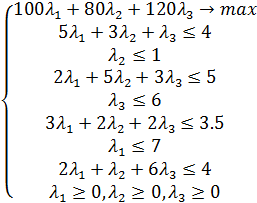
Для интерпретации двойственной задачи, предположим, что все требуемые витамины можно приобрести раздельно в аптеке. Вектор λ =(λ₁, λ₂, λ₃) – вектор цен на рассматриваемые витамины. Продавая суточный набор b = (100 80 120) по этим ценам, аптекарь получит доход, равный , который он старается максимизировать. Но его товар должен быть конкурентоспособен с наборами витаминов, содержащихся поливитаминах, поэтому, назначая цены, аптекарь должен следить за выполнением условий:

Еще нужно добавить ограничения λ₁≥0, λ₂≥ 0,λ₃≥0( следуют из экономического смысла)