Примеры решения задач
Пример: определить величину и точку приложения силы гидростатического давления воды на щит шириной b=2м, если глубина воды перед щитом H=2,7м.
Р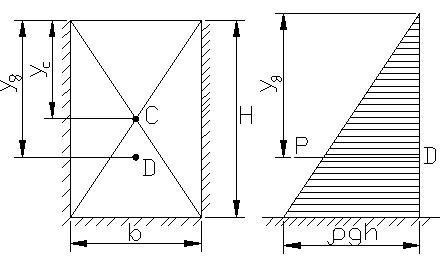
ешение:
Сила давления воды на
щит: рис.16
Расстояние точки приложения этой силы от свободной поверхности воды:
Пример: определить диаметр d суженной части трубы, при котором вода поднимается на высоту h=3,5м (рис. 17). Расход воды Q=6л/с, диаметр D=10см.
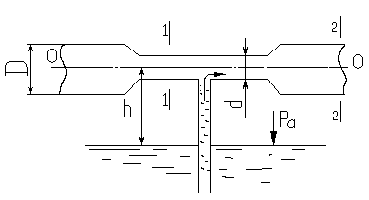
Рис.17
Решение:
Сечение1-1
принимаем в суженной части трубы, где
нужно определить d,
сечение 2-2 – на выходе из расширенной
части трубы, где давление равно
атмосферному (р2=ра).
Плоскость сравнения совместим с осью
трубы, тогда z1=z2=0.
С учетом этого уравнение Бернулли
получим в виде:
Для того чтобы вода поднялась из резервуара на высоту h, удельная энергия давления на поверхности воды в резервуаре ратм/ρg должна быть на величину h выше, чем удельная энергия давления в сечении 1-1, т.е.:
Решая совместно эти уравнения, получим:
Скорости воды в сечении 1-1 и 2-2:
;
Подставляя эти величины в последнее уравнение, и решая его относительно диаметра суженной части, получим:
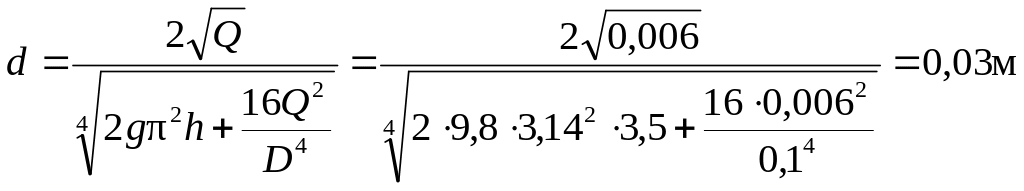
Пример: найти потерю давления на трение при движении воды с температурой Т=50˚С в цельносварной стальной трубе, бывшей в эксплуатации, с внутренним диаметром d=0,5м. Расход воды Q=0,6 м3/с. Длина трубы l=500 м.
Решение:
Находим по таблице значение абсолютной эквивалентной шероховатости трубы ∆экв=0,15 мм = 0,15∙10-3м, ∆экв /d=0,0003.
Кинематический коэффициент вязкости для воды заданной температуры ν=0,55∙10-6 м2/с.
Средняя скорость течения воды в трубе и число Рейнольдса:
Значение коэффициента гидравлического трения:
Потери напора на трение:
м.вод.ст.
Плотность воды находим из таблицы приложения по температуре – ρ=988 кг/м3.
Потери давления на трение:
Пример: вода при температуре Т=20˚С перекачивается насосом из открытого бака А в резервуар В (рис.15), где поддерживается постоянное давление РВ=0,075 МПа (избыточное) по трубопроводу общей длиной l=112м и диаметром d=125мм. Разность уровней воды в баках НГ=25м. Определить напор, создаваемый насосом для подачи в бак В расхода воды Q=25 л/с. Принять суммарный коэффициент местных сопротивлений ξ=6,5. Эквивалентная шероховатость стенок трубопровода ∆Э=0,15мм.
Решение:
Напор, создаваемый насосом:
Средняя скорость течения воды в трубе:
Число Рейнольдса для потока воды в трубе:
Значение коэффициента гидравлического трения
Величина напора:
Приложение
1. Средние значения плотности и кинематической
вязкости некоторых жидкостей
Жидкость
|
Плотность,кг/м3, при t,˚C |
Кинематическая вязкость, м2/с при t ,оС
|
||||
20
|
50
|
20
|
40
|
60
|
80
|
|
Вода пресная |
998 |
— |
0,010 |
0,0065 |
0,0047 |
0,003 |
Нефть Баку, легкая
|
884
|
—
|
0,25
|
—
|
—
|
—
|
Нефть Баку, тяжелая |
924
|
—
|
1,4
|
—
|
—
|
—
|
Бензин авиац.
|
745
|
—
|
0,0073 |
0,0059 |
0,0049
|
—
|
Керосин Т-1 (очищенный)
|
808 |
— |
0,025 |
0,018 |
0,012 |
0,010 |
Керосин Т-2 (тракторный) |
819 |
— |
0,010 |
— |
— |
— |
Дизельное топливо
|
846
|
—
|
0,28
|
0,12
|
—
|
—
|
Глицерин
|
1245
|
—
|
9,7
|
3,3
|
0,88
|
0,38
|
Ртуть
|
13550
|
—
|
0,0016
|
0,0014
|
0,0010
|
—
|
Масла:
|
|
|
|
|
|
|
Касторовое
|
960
|
—
|
15
|
3,5
|
0,88
|
0,35
|
Трансформаторное
|
884
|
880
|
0,28
|
0,13
|
0,076
|
0,084
|
АМГ-10
|
—
|
850
|
0,17
|
0,11
|
0,085
|
0,065
|
Веретенное АУ
|
—
|
892
|
6,48
|
0,19
|
0,098
|
0,059
|
Индустриальное 12
|
—
|
883
|
0,48
|
0,19
|
0,98
|
0,059
|
То же, 20
|
—
|
891
|
0,85
|
0,33
|
0,14
|
0,080
|
30
|
—
|
901
|
1,8
|
0,56
|
0,21
|
0,11
|
50
|
—
|
910
|
5,3
|
1,1
|
0,38
|
0,16
|
Турбинное
|
—
|
900
|
0,97
|
038
|
0,16
|
0,088
|
Автотракторное АКи-10
|
—
|
898
|
5,0
|
1,1
|
0,45
|
0,20
|