Задания

(Определяются последней цифрой шифра и

должны быть изложены на одной странице)

Последняя цифра шифра	Номер задачи
1	Т1, 1, 4, 7, 11
2	Т2, 2, 5, 7, 11
3	Т3, 3, 6, 8, 11
4	Т4, 1, 5, 9, 11
5	Т5, 2, 6, 8, 11
6	Т6, 3, 4. 9, 11
7	Т7, 1, 6, 7, 11
8	Т8, 2, 4, 9, 11
9	Т9, 3, 5, 10, 11
0	Т0, 1, 6, 10, 11

Задания по теории предмета

Т1. Пьезометрическая и вакуумметрическая высота. Пьезометрические плоскости.

Т2. Скорость и расход истечения жидкости через отверстие в тонкой стенке.

Т3. Сила гидростатического давления на криволинейную поверхность (как векторная сумма проекций на координатные оси).

Т4. Относительный покой жидкости в цилиндрическом сосуде, вращающемся относительно вертикальной оси.

Т5. Уравнение Бернулли для потока вязкой несжимаемой жидкости. Диаграмма уравнения на примерах.

Т6. Формулы для расчета потери напора в трубах. Зависимость коэффициента гидравлического трения от числа Рейнольдса и относительные шероховатости.

Т7. Основное уравнение гидростатики и закон Паскаля.

Т8. Числа подобия гидромеханики (критерии).

Т9. Действительные рабочие характеристики центробежного насоса.

Т10. Определение пропускной способности простого трубопровода.

Расчетные задачи Тема: Физические свойства жидкостей

Задача 1. Автоклав объемом 25л наполнен жидкостью и закрыт герметически, коэффициент температурного расширения жидкости , ее модуль упругости Е. Определить повышение давления в автоклаве при увеличении температуры жидкости на величину Т, объемной деформацией автоклава пренебречь.

шифр	1	2	3	4	5	6	7	8	9	0
, 10 -6 1/ оС	649	832	698	351	956	735	187	536	150	653
Е, 109 Па	1,58	1,95	1,67	2,08	1,48	1,72	2,46	2,08	2,06	1,75
Т, оС	40,5	11,0	38,5	45,0	19,9	32,0	5,5	21,0	39,5	32,5

Указания: При решении задачи используют известные формулы для определения коэффициентов объемного сжатия и температурного расширения жидкости. Интересно, что повышение давления в герметичном заполненном жидкостью сосуде не зависит от его объема.

Задача 2. Определить скорость υ равномерного скольжения прямоугольной пластины (aхbхс) по наклонной плоскости под углом = 12^о, если между пластиной и плоскостью находится слой масла толщиной (рис.7). Температура масла 30°С, плотность материала пластины =7850 кг/м³.

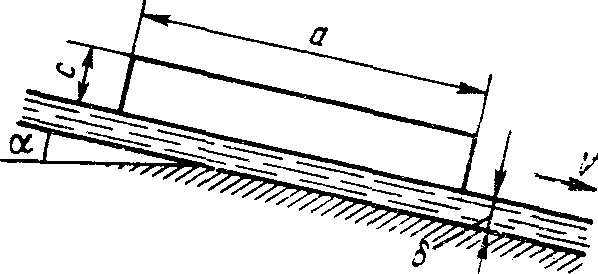
Рис.7

Шифр	1	2	3	4	5	6	7	8	9	0
Масло	Индустр-ное	Турбинное	Индустр-ное	Трансформато рное	АМГ-10	Индустр-ное	Касторовое	Веретенное	Индустр-ное	Турбинное
а, мм	580	400	590	530	470	630	310	850	720	450
в, мм	450	250	300	260	290	440	140	740	570	280
с, мм	12	43	10	13	20	11	15	7	6	35
, мм	0.4	0.7	1.1	0.5	0.4	0.9	1.2	0.6	0.5	0.9

Задача 3. Зазор между валом и втулкой заполнен маслом, толщина слоя которого равна . Диаметр вала D, длина втулки L. Вал вращается равномерно под воздействием вращающего момента М. Определить частоту вращения вала, если температура масла равна 40 °С.

Рис.8

Шифр	1	2	3	4	5	6	7	8	9	0
Масло	Индустр-ное	Турбинное	Индустр-ное	Трансформа торное	АМГ-10	Индустр-ное	Касторовое	Веретенное	Индустр-ное	Турбинное
М, Нм	520	1.35	9.20	4.50	2.65	3.30	15.5	6.10	1.65	8.50
, мм	3,3	0,8	2,2	1,5	1,1	1,7	2,8	5,1	1,4	1,9
D, мм	480	100	180	470	270	400	250	340	230	200
L, мм	1400	300	700	1200	780	640	1300	850	590	630

Указание: При решении задач 2,3 применяется формула Ньютона.

Поскольку толщина слоя масла мала, можно считать, что скорости в нем изменяются по прямолинейному закону. Эпюра касательных напряжений в слое масла принимается прямоугольной; сила трения проходит через центр тяжести этой эпюры. В задачах 2,3 важно увидеть параллель хода решения этих задач, и перед решением задачи 3 следует рассмотреть задачу 2. Задачи решаются с помощью формулы Ньютона:

T=A(dυ/dn),

где T- сила трения;

 - динамическая вязкость жидкости;

А - площадь соприкосновения твердой поверхности с жидкостью;

(dυ/dn) - градиент скорости. Пластина скользит под воздействием силы F= G sin , где G - сила тяжести пластины. При равномерном движении T=G и равна величине силы Р.

Задачу 3 решают по той же методике, с учетом законов вращательного движения. Силу трения в этом случае определяют из формулы момента:

М=Т( D/2 + /2)

Из-за малости зазора вторым членом в скобках можно пренебречь. Рассматривая движение в зазоре как плоскопараллельное, т.е. считая, что скорости в слое масла изменяются по прямолинейному закону, то угловую скорость  и частоту вращения вала n определяют по известным формулам механики:

υ= D/2, =2n