МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ДНІПРОДЗЕРЖИНСЬКИЙ ДЕРЖАВНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
МЕТОДИЧНІ ВКАЗІВКИ
до самостійної роботи з дисципліни
«Математичний аналіз»
(змістовий модуль 5)
для студентів, що навчаються за напрямом
6.040301 «Прикладна математика»
ЗАТВЕРДЖЕНО:
Редакційно-видавничою секцією
науково-методичної ради ДДТУ
“_____” _______ 20___ р. протокол №
Дніпродзержинськ
2012
Розповсюдження і тиражування без офіційного дозволу Дніпродзержинського державного технічного університету заборонено.
Методичні вказівки до самостійної роботи з дисципліни “Математичний аналіз” (змістовний модуль 5) для студентів, що навчаються за напрямом 6.040301 “Прикладна математика” / Укладач С.В.Тимченко – Дніпродзержинськ, ДДТУ, 2012. - 37 с.
Укладач: С.В.Тимченко, ст. викладач
Відповідальний за випуск: С.Є.Самохвалов,
проф., доктор техн. наук
Рецензент: В.В.Кармазина, к.ф.-м.наук, доцент
Затверджено на засіданні кафедри ПМ
протокол № 8 від 30 січня 2012 року
Коротка анотація до видання. У методичних вказівках до самостійної роботи з дисципліни «математичний аналіз» (змістовний модуль 5) наведено варіанти індивідуальних завдань для модульного контролю. Наведено зразок виконання індивідуального завдання.
ЗМІСТ
Вступ . . . . . . . . . . . . . . . . . . . . . . |
. . . . . 4 |
Варіант 1 . . . . . . . . . . . . . . . . . . . . |
. . . . . 5 |
Варіант 2 . . . . . . . . . . . . . . . . . . . . |
. . . . . 6 |
Варіант 3 . . . . . . . . . . . . . . . . . . . . |
. . . . . 7 |
Варіант 4 . . . . . . . . . . . . . . . . . . . . |
. . . . . 8 |
Варіант 5 . . . . . . . . . . . . . . . . . . . . |
. . . . . 9 |
Варіант 6 . . . . . . . . . . . . . . . . . . . . |
. . . . . 10 |
Варіант 7 . . . . . . . . . . . . . . . . . . . . |
. . . . . 11 |
Варіант 8 . . . . . . . . . . . . . . . . . . . . |
. . . . . 12 |
Варіант 9 . . . . . . . . . . . . . . . . . . . . |
. . . . . 13 |
Варіант 10 . . . . . . . . . . . . . . . . . . . . |
. . . . . 14 |
Варіант 11 . . . . . . . . . . . . . . . . . . . . |
. . . . . 15 |
Варіант 12 . . . . . . . . . . . . . . . . . . . . |
. . . . . 16 |
Варіант 13 . . . . . . . . . . . . . . . . . . . . |
. . . . . 17 |
Варіант 14 . . . . . . . . . . . . . . . . . . . . |
. . . . . 18 |
Варіант 15 . . . . . . . . . . . . . . . . . . . . |
. . . . . 19 |
Варіант 16 . . . . . . . . . . . . . . . . . . . . |
. . . . . 20 |
Варіант 17 . . . . . . . . . . . . . . . . . . . . |
. . . . . 21 |
Варіант 18 . . . . . . . . . . . . . . . . . . . . |
. . . . . 22 |
Варіант 19 . . . . . . . . . . . . . . . . . . . . |
. . . . . 23 |
Варіант 20 . . . . . . . . . . . . . . . . . . . . |
. . . . . 24 |
Зразок виконання індивідуального завдання . |
. . . . . 25 |
Перелік літератури . . . . . . . . . . . . . . . |
. . . . . 37 |
ВСТУП
Важливим елементом засвоєння математики й оволодіння її методами є самостійна робота студентів. Ця робота є неперервною складовою виконання поточних домашніх завдань і циклічної роботи з виконання індивідуальних модульних завдань. Результативність самостійної роботи студентів забезпечується ефективною системою контролю, яка включає опитування студентів за змістом лекції, перевірку виконання поточних домашніх завдань, розв’язування задач біля дошки, захист індивідуальних модульних робіт.
Метою індивідуальних домашніх завдань є перевірка результативності самостійної роботи з даного модуля.
Студент повинен самостійно розв’язати індивідуальні домашні завдання свого варіанта, який відповідає номеру студента у списку навчальної групи.
Розв’язання завдань із поясненнями слід подати у зошиті, на обкладинці якого необхідно написати назву дисципліни та модуля; прізвище студента, його ім’я і по батькові; курс, номер групи; номер варіанта. Кожне завдання необхідно позначати його номером за методичними вказівками. Умову завдання треба переписати повністю.
Якщо після перевірки роботи викладачем зроблені зауваження, студент повинен розв’язати заново неправильно виконані завдання у тому самому зошиті і повторно подати його на перевірку. Після позитивної оцінки викладача робота підлягає захисту.
ВАРІАНТ 1
Завдання
1.
Знайти частинні похідні
та
від заданих функцій:
а)
; б)
;
в)
; г)
.
Завдання
2.
Перевірити, чи задовольняє функція
умові
.
Завдання
3. Знайти
та
,
якщо
,
,
.
Завдання
4.
Обчислити наближено:
.
Завдання
5.
Обчислити
,
якщо
.
Завдання
6.
Знайти
похідну скалярного поля
в точці М
за напрямом вектора l
:
, М
(1; 1; 1) , 
.
Завдання 7. Знайти похідну функції в точці М за напрямом нормалі до поверхні S, яка утворює гострий кут з додатнім напрямом осі Oz.
,
,
.
Завдання
8.
Знайти кут між градієнтами скалярних
полів
і
в точці М.
,
;
.
Завдання 9. Дослідити задану функцію на екстремум
.
Завдання
10.
Знайти екстремум функції
при умові
.
ВАРІАНТ 2
Завдання 1. Знайти частинні похідні та від заданих функцій:
а)
; б)
;
в)
; г)
.
Завдання
2.
Перевірити, що функція
задовольняє
умові
.
Завдання
3.
Знайти
,
якщо
,
,
.
Завдання
4.
Обчислити наближено:
.
Завдання
5. Знайти
,
якщо
.
Завдання 6. Знайти похідну скалярного поля в точці М за напрямом вектора l .
,
М
(2; 1; 1) ,
.
Завдання 7. Знайти похідну функції в точці М за напрямом нормалі до поверхні S, яка утворює гострий кут з додатнім напрямом осі Oz.
,
,
.
Завдання 8. Знайти кут між градієнтами скалярних полів і в точці М.
, 
; 
.
Завдання 9. Дослідити задану функцію на екстремум
.
Завдання
10.
Знайти екстремум функції
при умові
.
ВАРІАНТ 3
Завдання 1. Знайти частинні похідні та від заданих функцій:
а)
;
б)
;
в)
;
г)
.
Завдання
2.
Перевірити, що функція
задовольняє умові
.
Завдання
3. Знайти
та
,
якщо
,
,
.
Завдання
4.
Обчислити наближено:
.
Завдання
5. Довести,
що
,
якщо
.
Завдання 6. Знайти похідну скалярного поля в точці М за напрямом вектора l .
,
М
(1; 5; -2) , 
.
Завдання 7. Знайти похідну функції в точці М за напрямом нормалі до поверхні S, яка утворює гострий кут з додатнім напрямом осі Oz.
,
,
.
Завдання 8. Знайти кут між градієнтами скалярних полів і в точці М.
,
; 
.
Завдання 9. Дослідити задану функцію на екстремум
.
Завдання
10.
Знайти екстремум функції
при умові
.
ВАРІАНТ 4
Завдання 1. Знайти частинні похідні та від заданих функцій:
а)
;
б)
;
в)
; г)
.
Завдання
2.
Перевірити, що функція
задовольняє
умові
.
Завдання
3.
Знайти
,
якщо
,
,
.
Завдання
4.
Обчислити наближено:
.
Завдання
5.
Обчислити
,
якщо
.
Завдання 6. Знайти похідну скалярного поля в точці М за напрямом вектора l .
, М
(0; 1; 1) , 
.
Завдання 7. Знайти похідну функції в точці М за напрямом нормалі до поверхні S, яка утворює гострий кут з додатнім напрямом осі Oz.
,
,
.
Завдання 8. Знайти кут між градієнтами скалярних полів і в точці М.
, 
;
.
Завдання 9. Дослідити задану функцію на екстремум
.
Завдання
10.
Знайти екстремум функції
при умові
.
ВАРІАНТ 5
Завдання 1. Знайти частинні похідні та від заданих функцій:
а)
;
б)
;
в)
; г)
.
Завдання
2.
Перевірити, що функція
задовольняє
умові
.
Завдання
3. Знайти
та
,
якщо
,
,
.
Завдання
4.
Обчислити наближено:
.
Завдання
5. Знайти
,
якщо
.
Завдання 6. Знайти похідну скалярного поля в точці М за напрямом вектора l .
, М
(-2; 1; -1) , 
.
Завдання 7. Знайти похідну функції в точці М за напрямом нормалі до поверхні S, яка утворює гострий кут з додатнім напрямом осі Oz.
,
,
.
Завдання 8. Знайти кут між градієнтами скалярних полів і в точці М.
, 
; 
.
Завдання 9. Дослідити задану функцію на екстремум
.
Завдання
10.
Знайти екстремум функції
при умові
.
ВАРІАНТ 6
Завдання 1. Знайти частинні похідні та від заданих функцій:
а)
; б)
;
в)
; г)
.
Завдання
2.
Перевірити, що функція
задовольняє умові
.
Завдання
3.
Знайти
,
якщо
,
.
Завдання
4.
Обчислити наближено:
.
Завдання
5. Довести,
що
,
якщо
.
Завдання 6. Знайти похідну скалярного поля в точці М за напрямом вектора l .
,
М
(1; 3; 2) , 
.
Завдання 7. Знайти похідну функції в точці М за напрямом нормалі до поверхні S, яка утворює гострий кут з додатнім напрямом осі Oz.
,
,
.
Завдання 8. Знайти кут між градієнтами скалярних полів і в точці М.
; 
;
.
Завдання 9. Дослідити задану функцію на екстремум
.
Завдання
10.
Знайти екстремум функції
при умові
.
ВАРІАНТ 7
Завдання 1. Знайти частинні похідні та від заданих функцій:
а)
; б)
;
в)
; г)
.
Завдання
2.
Перевірити, що функція
задовольняє
умові
.
Завдання
3. Знайти
та
,
якщо
,
,
.
Завдання
4.
Обчислити наближено:
.
Завдання
5.
Обчислити
,
якщо
.
Завдання 6. Знайти похідну скалярного поля в точці М за напрямом вектора l .
,
М
(
)
,
.
Завдання 7. Знайти похідну функції в точці М за напрямом нормалі до поверхні S, яка утворює гострий кут з додатнім напрямом осі Oz.
,
,
.
Завдання 8. Знайти кут між градієнтами скалярних полів і в точці М.
, 
, 
.
Завдання 9. Дослідити задану функцію на екстремум
.
Завдання
10.
Знайти екстремум функції
при умові
.
ВАРІАНТ 8
Завдання 1. Знайти частинні похідні та від заданих функцій:
а)
; б)
;
в)
; г)
.
Завдання 2. Перевірити, що задана функція задовольняє умові
,
якщо
.
Завдання
3.
Знайти
,
якщо
,
,
.
Завдання
4.
Обчислити наближено:
.
Завдання
5. Знайти
,
якщо
.
Завдання 6. Знайти похідну скалярного поля в точці М за напрямом вектора l .
,
М
(1; 1; 2) , 
.
Завдання 7. Знайти похідну функції в точці М за напрямом нормалі до поверхні S, яка утворює гострий кут з додатнім напрямом осі Oz.
,
,
.
Завдання 8. Знайти кут між градієнтами скалярних полів і в точці М.
,
,
.
Завдання 9. Дослідити задану функцію на екстремум
.
Завдання
10.
Знайти екстремум функції
при умові
.
ВАРІАНТ 9
Завдання 1. Знайти частинні похідні та від заданих функцій:
а)
; б)
;
в)
; г)
.
Завдання
2.
Перевірити, що функція
задовольняє
умові
.
Завдання
3. Знайти
та
,
якщо
,
,
.
Завдання
4.
Обчислити наближено:
.
Завдання
5. Довести,
що
,
якщо
.
Завдання 6. Знайти похідну скалярного поля в точці М за напрямом вектора l .
,
М
(1; -3; 4) , 
.
Завдання 7. Знайти похідну функції в точці М за напрямом нормалі до поверхні S, яка утворює гострий кут з додатнім напрямом осі Oz.
,
,
.
Завдання 8. Знайти кут між градієнтами скалярних полів і в точці М.
,
,
.
Завдання 9. Дослідити задану функцію на екстремум
.
Завдання
10.
Знайти екстремум функції
при умові
.
ВАРІАНТ 10
Завдання 1. Знайти частинні похідні та від заданих функцій:
а)
; б)
;
в)
; г)
.
Завдання
2.
Перевірити,
що функція
задовольняє
умові
.
Завдання
3.
Знайти
,
якщо
,
.
Завдання
4.
Обчислити наближено:
.
Завдання
5.
Обчислити
,
якщо
.
Завдання 6. Знайти похідну скалярного поля в точці М за напрямом вектора l .
,
М
(4; 1; -2) , 
.
Завдання 7. Знайти похідну функції в точці М за напрямом нормалі до поверхні S, яка утворює гострий кут з додатнім напрямом осі Oz.
,
,
.
Завдання 8. Знайти кут між градієнтами скалярних полів і в точці М.
, 
; 
.
Завдання 9. Дослідити задану функцію на екстремум
.
Завдання
10.
Знайти екстремум функції
при умові
.
ВАРІАНТ 11
Завдання 1. Знайти частинні похідні та від заданих функцій:
а)
; б)
;
в)
; г)
.
Завдання
2.
Перевірити, що функція
задовольняє
умові
.
Завдання
3. Знайти
та
,
якщо
,
,
.
Завдання
4.
Обчислити наближено:
.
Завдання
5. Знайти
,
якщо
.
Завдання 6. Знайти похідну скалярного поля в точці М за напрямом вектора l .
, М
(1; 1; 0) , 
.
Завдання 7. Знайти похідну функції в точці М за напрямом нормалі до поверхні S, яка утворює гострий кут з додатнім напрямом осі Oz.
,
,
.
Завдання 8. Знайти кут між градієнтами скалярних полів і в точці М.
,
, 
.
Завдання 9. Дослідити задану функцію на екстремум
.
Завдання
10.
Знайти екстремум функції
при умові
.
ВАРІАНТ 12
Завдання 1. Знайти частинні похідні та від заданих функцій:
а)
; б)
;
в)
; г)
.
Завдання
2.
Перевірити, що функція
задовольняє умові
.
Завдання
3.
Знайти
,
якщо
,
,
.
Завдання
4.
Обчислити наближено:
.
Завдання
5. Довести,
що
,
якщо
.
Завдання 6. Знайти похідну скалярного поля в точці М за напрямом вектора l .
,
М
(3; -2; 1) , 
.
Завдання 7. Знайти похідну функції в точці М за напрямом нормалі до поверхні S, яка утворює гострий кут з додатнім напрямом осі Oz.
,
,
.
Завдання 8. Знайти кут між градієнтами скалярних полів і в точці М.
,
,
.
Завдання 9. Дослідити задану функцію на екстремум
.
Завдання
10.
Знайти екстремум функції
при умові
.
ВАРІАНТ 13
Завдання 1. Знайти частинні похідні та від заданих функцій:
а) ; б) ;
в)
;
г)
.
Завдання
2.
Перевірити, що функція
задовольняє
умові
.
Завдання
3. Знайти
та
,
якщо
,
,
.
Завдання
4.
Обчислити наближено:
.
Завдання
5.
Обчислити
,
якщо
.
Завдання 6. Знайти похідну скалярного поля в точці М за напрямом вектора l .
, М
(1; 2; -1) , 
.
Завдання 7. Знайти похідну функції в точці М за напрямом нормалі до поверхні S, яка утворює гострий кут з додатнім напрямом осі Oz.
,
,
.
Завдання 8. Знайти кут між градієнтами скалярних полів і в точці М.
,
; 
.
Завдання 9. Дослідити задану функцію на екстремум
.
Завдання
10.
Знайти екстремум функції
при умові
.
ВАРІАНТ 14
Завдання 1. Знайти частинні похідні та від заданих функцій:
а)
; б)
;
в) ; г) .
Завдання 2. Перевірити, що функція задовольняє умові
.
Завдання
3.
Знайти
,
якщо
,
.
Завдання
4.
Обчислити наближено:
.
Завдання
5. Знайти
,
якщо
.
Завдання 6. Знайти похідну скалярного поля в точці М за напрямом вектора l .
, М
(1; -1; 2) , 
.
Завдання 7. Знайти похідну функції в точці М за напрямом нормалі до поверхні S, яка утворює гострий кут з додатнім напрямом осі Oz.
,
,
.
Завдання 8. Знайти кут між градієнтами скалярних полів і в точці М.
,
, 
.
Завдання 9. Дослідити задану функцію на екстремум
.
Завдання
10.
Знайти екстремум функції
при умові
.
ВАРІАНТ 15
Завдання 1. Знайти частинні похідні та від заданих функцій:
а) ; б) ;
в) ; г) .
Завдання
2.
Перевірити, що функція
задовольняє
умові
.
Завдання
3. Знайти
та
,
якщо
,
,
.
Завдання
4.
Обчислити наближено:
.
Завдання
5. Довести,
що
,
якщо
.
Завдання 6. Знайти похідну скалярного поля в точці М за напрямом вектора l .
,
М
(-4; 3; -1) ,
.
Завдання 7. Знайти похідну функції в точці М за напрямом нормалі до поверхні S, яка утворює гострий кут з додатнім напрямом осі Oz.
, , .
Завдання 8. Знайти кут між градієнтами скалярних полів і в точці М.
;
;
.
Завдання 9. Дослідити задану функцію на екстремум
.
Завдання
10.
Знайти екстремум функції
при умові
.
ВАРІАНТ 16
Завдання 1. Знайти частинні похідні та від заданих функцій:
а) ; б) ;
в) ; г) .
Завдання 2. Перевірити, що задана функція задовольняє умові
,
якщо
.
Завдання
3.
Знайти
,
якщо
,
.
Завдання
4.
Обчислити наближено:
.
Завдання
5.
Обчислити
,
якщо
.
Завдання 6. Знайти похідну скалярного поля в точці М за напрямом вектора l .
,
М
(1; -3; 4) ,
.
Завдання 7. Знайти похідну функції в точці М за напрямом нормалі до поверхні S, яка утворює гострий кут з додатнім напрямом осі Oz.
,
,
.
Завдання 8. Знайти кут між градієнтами скалярних полів і в точці М.
,
,
.
Завдання 9. Дослідити задану функцію на екстремум
.
Завдання 10. Знайти екстремум функції при умові .
ВАРІАНТ 17
Завдання 1. Знайти частинні похідні та від заданих функцій:
а) ; б) ;
в) ; г) .
Завдання
2.
Перевірити, що функція
задовольняє
умові
.
Завдання
3. Знайти
та
,
якщо
,
,
.
Завдання
4.
Обчислити наближено:
.
Завдання
5. Знайти
,
якщо
.
Завдання 6. Знайти похідну скалярного поля в точці М за напрямом вектора l .
,
М
(2; 1; 1) , 
.
Завдання 7. Знайти похідну функції в точці М за напрямом нормалі до поверхні S, яка утворює гострий кут з додатнім напрямом осі Oz.
,
,
.
Завдання 8. Знайти кут між градієнтами скалярних полів і в точці М.
,
,
.
Завдання 9. Дослідити задану функцію на екстремум
.
Завдання 10. Знайти екстремум функції при умові .
ВАРІАНТ 18
Завдання 1. Знайти частинні похідні та від заданих функцій:
а) ; б) ;
в) ; г) .
Завдання 2. Перевірити, що функція задовольняє умові
.
Завдання
3.
Знайти
,
якщо
,
,
.
Завдання
4.
Обчислити наближено:
.
Завдання
5. Довести,
що
,
якщо
.
Завдання 6. Знайти похідну скалярного поля в точці М за напрямом вектора l .
, М (1; 1; 1) , .
Завдання 7. Знайти похідну функції в точці М за напрямом нормалі до поверхні S, яка утворює гострий кут з додатнім напрямом осі Oz.
,
,
.
Завдання 8. Знайти кут між градієнтами скалярних полів і в точці М.
,
,
.
Завдання 9. Дослідити задану функцію на екстремум
.
Завдання 10. Знайти екстремум функції при умові .
ВАРІАНТ 19
Завдання 1. Знайти частинні похідні та від заданих функцій:
а) ; б) ;
в) ; г) .
Завдання 2. Перевірити, що задана функція задовольняє умові
,
якщо
.
Завдання
3. Знайти
та
,
якщо
,
,
.
Завдання
4.
Обчислити наближено:
.
Завдання
5.
Обчислити
,
якщо
.
Завдання 6. Знайти похідну скалярного поля в точці М за напрямом вектора l .
, М (2; 1; 1) , .
Завдання 7. Знайти похідну функції в точці М за напрямом нормалі до поверхні S, яка утворює гострий кут з додатнім напрямом осі Oz.
,
,
.
Завдання 8. Знайти кут між градієнтами скалярних полів і в точці М.
,
;
.
Завдання 9. Дослідити задану функцію на екстремум
.
Завдання 10. Знайти екстремум функції при умові .
ВАРІАНТ 20
Завдання 1. Знайти частинні похідні та від заданих функцій:
а) ; б) ;
в) ; г) .
Завдання 2. Перевірити, що задана функція задовольняє умові
,
якщо
.
Завдання
3.
Знайти
,
якщо
,
.
Завдання
4.
Обчислити наближено:
.
Завдання
5. Знайти
,
якщо
.
Завдання 6. Знайти похідну скалярного поля в точці М за напрямом вектора l .
, М (1; 5; -2) , .
Завдання 7. Знайти похідну функції в точці М за напрямом нормалі до поверхні S, яка утворює гострий кут з додатнім напрямом осі Oz.
,
,
.
Завдання 8. Знайти кут між градієнтами скалярних полів і в точці М.
,
, 
.
Завдання 9. Дослідити задану функцію на екстремум
.
Завдання 10. Знайти екстремум функції при умові .
Зразок виконання індивідуального завдання
Завдання 1. Знайти частинні похідні та від заданих функцій:
а)
; б)
;
в)
; г)
.
Розв'язання
а) Для функції маємо
та
.
б)
Функція
представляє собою добуток, тому
;
;
в) Функція представляє собою частку, тому
;
.
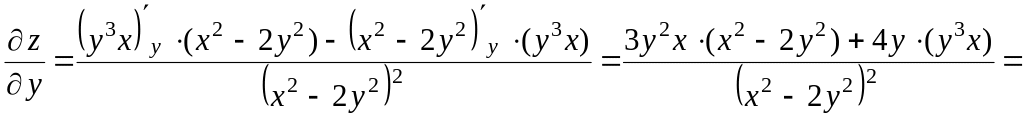
г) Функція є складеною, тому отримуємо
;
.
Завдання
2.
Перевірити, що функція
задовольняє умові
.
Розв'язання
Знайдемо частинні похідні та від заданої функції :
;
.
Знайдені вирази підставимо у задане рівняння, отримаємо
,
,
;
,
що і треба було довести.
Завдання
3. Знайти
та
,
якщо
,
,
.
Розв'язання
Задана
функції
є складеною, де кожен аргумент в свою
чергу є функцією двох змінних
,
.
Для знаходження частинних похідних
та
скористаємося формулами:
; 
.
(1)
Знайдемо відповідні частинні похідні для кожної із заданих функцій. Для функції маємо:
;
.
Для функції маємо наступні частинні похідні:
;
.
Для функції частинні похідні мають вигляд:
; 
.
Знайдені частинні похідні підставляємо у формули (1), отримуємо
;
.
Завдання
4.
Обчислити наближено:
.
Розв'язання
Для наближеного обчислення застосовуємо формулу:
.
(2)
Заданою
функцією є
.
З умови маємо:
,
тоді
,
і
,
,
отже точка
має координати
і значення функції в цій точці дорівнює
.
Знайдемо частинні похідні від заданої функції:
;
.
Обчислимо
значення цих похідних в точці
:
;
.
Знайдені величини підставляємо у формулу (2), отримуємо
.
Завдання
5. Довести,
що
,
якщо
.
Розв'язання
Для заданої функції знайдемо вказані частинні похідні:
; 
;
.
Знайдені похідні підставляємо в умову, отримуємо
,
,
що і треба було довести.
Завдання
6.
Знайти
похідну скалярного поля
в точці М
за напрямом вектора
.
, М
(1; 1; 1) , 
.
Розв'язання
Якщо
функція
є диференційованою, то похідна за
напрямом обчислюється за формулою:
.
Знайдемо частинні похідні від заданої функції та обчислимо їх значення в заданій точці. Маємо
; 
;
; 
;
;
.
Знайдемо
напрямні
косинуси вектора
.
Довжина вектора
,
тоді
,
,
.
Таким чином,
.
Завдання 7. Знайти похідну функції в точці М за напрямом нормалі до поверхні S, яка утворює гострий кут з додатнім напрямом осі Oz.
,
,
.
Розв'язання
Спочатку
знайдемо координати вектора нормалі
до заданої поверхні. Рівняння поверхні
задано у неявній формі
,
тому вектор нормалі має координати
.
Знаходимо
частинні похідні від функції
та їх значення в точці М:
, 
,
;
,
,
.
Таким
чином, нормальним вектором до поверхні
є
.
Знаходимо його довжину та напрямні
косинуси:
,
,
,
.
Знайдемо
частинні похідні від функції
та обчислимо їх значення в точці М:
; 
;
; 
;
;
.
Отже,
,
.
Завдання 8. Знайти кут між градієнтами скалярних полів і в точці М.
,
,
.
Розв'язання
Градієнтом
функції
в точці М
називають вектор, координати якого є
значення частинних похідних функції у
заданій точці і позначають
.
Отже,
.
Знайдемо частинні похідні заданих функцій та обчислимо їх значення в заданій точці. Маємо для функції :
;
;
; 
;
;
,
Отже,
.
Аналогічно, для функції отримуємо:
;
;
; 
;
;
,
Отже,
.
Позначимо
через
та
і нагадаємо, що кут між векторами
знаходимо за формулою
.
Знайдемо довжину кожного з векторів:
,
,
тоді
.
Завдання 9. Дослідити задану функцію на екстремум
.
Розв'язання
Знайдемо стаціонарні точки функції, скористаємося необхідною умовою екстремуму функції двох змінних, а саме:
Маємо
;
,
тоді система набуває вигляду
Розв’язком
системи є
,
,
отже, функція має одну стаціонарну точку
М(0,
3).
Для дослідження характеру екстремуму використовуємо достатні умови. Знайдемо величину
.
Оскільки
,
,
,
то
.
Таким
чином,
,
,
отже точка М – точка максимуму. В цій
точці
.
Завдання
10.
Знайти найбільше значення функції
,
якщо х
та у
додатні і задовольняють рівняння зв’язку
.