
- •Лекція № 6. Невласні інтеграли. Застосування визначеного інтеграла до розв’язання задач геометрії та фізики.
- •1. Невласні інтеграли з нескінченними межами інтегрування (невласні інтеграли 1-го роду).
- •Ознаки збіжності невласних інтегралів 1-го роду.
- •2. Невласні інтеграли від необмежених функцій (невласні інтеграли 2-го роду)
- •Ознаки збіжності невласних інтегралів 2-го роду.
- •1) Якщо інтеграл збігається, то збігається й інтеграл .
- •3. Обчислення площ плоских фігур
- •1) Площа плоскої фігури в декартовій системі координат
- •2) Площа плоскої фігури при параметричному заданні межі області
- •3) Площа плоскої фігури в полярній системі координат
- •4. Обчислення довжини дуги гладкої кривої
- •1) Довжина дуги в декартовій системі координат
- •2) Довжина дуги кривої, заданої параметрично
- •3) Довжина дуги в полярній системі координат
- •5. Обчислення об’єму тіла.
- •6. Обчислення об’єму тіла обертання
- •6. Обчислення площі поверхні обертання
- •7. Обчислення роботи
3) Площа плоскої фігури в полярній системі координат
Розглянемо
плоску фігуру, обмежену кривою, заданою
в полярній системі координат неперервною
функцією
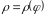 і променями
і променями
 і
і
 .
Таку фігуру називають криволінійним
сектором.
.
Таку фігуру називають криволінійним
сектором.
Обчислимо
площу
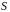 криволінійного сектора.
криволінійного сектора.
Р озіб’ємо
відрізок
на
озіб’ємо
відрізок
на
 частин
частин
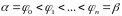 .
.
Через
кожну точку
 ,
проведемо промінь. Ці промені розіб’ють
сектор на
елементарних секторів. Очевидно, що
площа
всього сектора дорівнює сумі всіх площ
,
проведемо промінь. Ці промені розіб’ють
сектор на
елементарних секторів. Очевидно, що
площа
всього сектора дорівнює сумі всіх площ
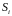 елементарних секторів.
елементарних секторів.
В кожному
відрізку
 виберемо довільну точку
виберемо довільну точку
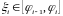 .
Площа
.
Площа
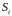 елементарного сектора, обмеженого
кривою
і променями
елементарного сектора, обмеженого
кривою
і променями
 і
і
 наближено дорівнює площі кругового
сектора, обмеженого тими самими променями
і дугою кола радіуса
наближено дорівнює площі кругового
сектора, обмеженого тими самими променями
і дугою кола радіуса
 :
:
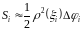 ,
де
,
де

Побудуємо
суму
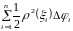 .
Ця сума буде інтегральною сумою функції
.
Ця сума буде інтегральною сумою функції
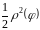 ,
яка відповідає даному розбиттю відрізка
і даному вибору проміжних точок
,
яка відповідає даному розбиттю відрізка
і даному вибору проміжних точок
 .
Тоді
.
Тоді
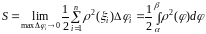 .
.
Отже, площа криволінійного сектора обчислюється за формулою:
 (4)
(4)
4. Обчислення довжини дуги гладкої кривої
1) Довжина дуги в декартовій системі координат
Нехай
 дуга кривої, заданої рівнянням
,
де
– неперервної на відрізку
функція.
дуга кривої, заданої рівнянням
,
де
– неперервної на відрізку
функція.
Д овжиною
дуги кривої
називається границя, до якої прямує
довжина вписаної до неї ламаної, коли
найбільша з її ланок прямує до 0.
овжиною
дуги кривої
називається границя, до якої прямує
довжина вписаної до неї ламаної, коли
найбільша з її ланок прямує до 0.
Обчислимо довжину ламаної:


або
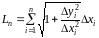 .
.
За
формулою Лагранжа
 ,
де
,
де
 . Отже, сума
. Отже, сума
 буде інтегральною сумою функції
буде інтегральною сумою функції
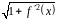 .
Таким чином, довжина
дуги кривої
обчислюється за формулою:
.
Таким чином, довжина
дуги кривої
обчислюється за формулою:
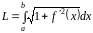 (5)
(5)
2) Довжина дуги кривої, заданої параметрично
Якщо крива задана параметрично
,
то
 (6)
(6)
Довжину дуги гладкої просторової кривої, заданої рівняннями

обчислюють за аналогічною формулою:

3) Довжина дуги в полярній системі координат
Нехай
крива в полярній системі координат
задана рівнянням
,
де
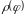 – неперервна на відрізку
функція. Якщо в рівностях
– неперервна на відрізку
функція. Якщо в рівностях
 ,
,
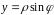 параметром вважати кут
параметром вважати кут
 ,
то
,
то
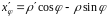 ,
,
 і
і
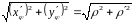 ,
тому за формулою (6)
,
тому за формулою (6)
 (7)
(7)
5. Обчислення об’єму тіла.
Нехай в нас є деяке тіло і нехай відомі площі перерізів цього тіла площинами, перпендикулярними до, наприклад, осі :

Тоді
утворені між перерізами тіла можна
вважати циліндрами з основами
і висотами
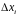 .
Очевидно, що об’єм
.
Очевидно, що об’єм
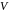 всього тіла дорівнює сумі всіх об’ємів
елементарних циліндрів.
всього тіла дорівнює сумі всіх об’ємів
елементарних циліндрів.
Побудуємо
суму
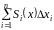 .
Ця сума буде інтегральною сумою функції
.
Ця сума буде інтегральною сумою функції
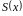 .
Тоді
.
Тоді
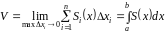 .
.
Отже,
об’єм тіла обчислюється за формулою:
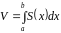 , (8)
, (8)
яка називається формулою об’єму тіла за площами паралельних перерізів.
6. Обчислення об’єму тіла обертання
Розглянемо, зокрема, об’єм тіла обертання. Нехай в нас є криволінійна трапеція, яка обмежена двома вертикальними прямими і , віссю і графіком невід’ємної і неперервної на відрізку функції . Якщо цю трапецію обертати навколо осі , то утвориться просторова фігура, яка називається тілом обертання:
О скільки
площі паралельних перерізів
скільки
площі паралельних перерізів
 ,
то за формулою (8), об’єм тіла, утвореного
обертанням даної криволінійної трапеції
навколо осі
,
то за формулою (8), об’єм тіла, утвореного
обертанням даної криволінійної трапеції
навколо осі
 . (9)
. (9)
Якщо
криволінійна трапеція обмежена двома
вертикальними прямими
 і
і
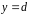 ,
віссю
,
віссю
 і графіком невід’ємної і неперервної
на відрізку
і графіком невід’ємної і неперервної
на відрізку
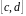 функції
функції
 ,
то об’єм тіла, утвореного обертанням
даної криволінійної трапеції навколо
осі
,
то об’єм тіла, утвореного обертанням
даної криволінійної трапеції навколо
осі
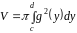 (10)
(10)
