
- •Лекція № 6. Невласні інтеграли. Застосування визначеного інтеграла до розв’язання задач геометрії та фізики.
- •1. Невласні інтеграли з нескінченними межами інтегрування (невласні інтеграли 1-го роду).
- •Ознаки збіжності невласних інтегралів 1-го роду.
- •2. Невласні інтеграли від необмежених функцій (невласні інтеграли 2-го роду)
- •Ознаки збіжності невласних інтегралів 2-го роду.
- •1) Якщо інтеграл збігається, то збігається й інтеграл .
- •3. Обчислення площ плоских фігур
- •1) Площа плоскої фігури в декартовій системі координат
- •2) Площа плоскої фігури при параметричному заданні межі області
- •3) Площа плоскої фігури в полярній системі координат
- •4. Обчислення довжини дуги гладкої кривої
- •1) Довжина дуги в декартовій системі координат
- •2) Довжина дуги кривої, заданої параметрично
- •3) Довжина дуги в полярній системі координат
- •5. Обчислення об’єму тіла.
- •6. Обчислення об’єму тіла обертання
- •6. Обчислення площі поверхні обертання
- •7. Обчислення роботи
Лекція № 6. Невласні інтеграли. Застосування визначеного інтеграла до розв’язання задач геометрії та фізики.
План лекції:
Невласні інтеграли з нескінченними мéжами інтегрування.
2. Невласні інтеграли від необмежених функцій.
3. Обчислення площ плоских фігур.
4. Обчислення довжини дуги гладкої кривої.
5. Обчислення об’єму тіла.
6. Обчислення площі поверхні обертання.
7. Обчислення роботи.
Поняття визначеного інтеграла можна узагальнити на випадок нескінченного проміжку інтегрування або на випадок необмеженої підінтегральної функції. Це узагальнення приводить до поняття невласного інтеграла.
1. Невласні інтеграли з нескінченними межами інтегрування (невласні інтеграли 1-го роду).
Визначення.
Нехай
функція
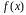 визначена на нескінченному проміжку
визначена на нескінченному проміжку
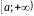 і інтегрована на відрізку
і інтегрована на відрізку
 ,
де
,
де
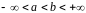 .
Границя
.
Границя
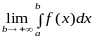 ,
називається невласним
інтегралом першого роду
і позначається
,
називається невласним
інтегралом першого роду
і позначається
 , тобто
, тобто

Якщо ця границя існує і скінченна, то інтеграл називається збіжним, якщо границя не існує або нескінченна, то – розбіжним.
Аналогічно визначається поняття невласного інтеграла 1-го роду вигляду
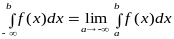 .
.
Визначення.
Нехай
функція
визначена на всій числовій прямій
 і інтегрована на кожному скінченому
відрізку
.
Границя
і інтегрована на кожному скінченому
відрізку
.
Границя
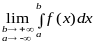 ,
називається невласним
інтегралом
1-го роду по числовій прямій
і позначається
,
називається невласним
інтегралом
1-го роду по числовій прямій
і позначається
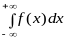 ,
тобто
,
тобто

Якщо ця границя існує і скінчена, то інтеграл називається збіжним, якщо не існує або нескінченна – розбіжним. Цей інтеграл зводиться до перших двох:
 .
.
Зауваження.
В останньому означенні межі інтегрування
повинні прямувати до
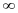 незалежно одна від одної.
незалежно одна від одної.
З наведених визначень випливає, що невласний інтеграл не є границею інтегральних сум, а є інтеграл визначеного інтеграла із змінною межею інтегрування.
Геометричний
зміст інтеграла
,
коли
неперервна і невід’ємна на
 і коли інтеграл збігається полягає в
тому, що
і коли інтеграл збігається полягає в
тому, що
 дорівнює площі необмеженої області.
дорівнює площі необмеженої області.

Ознаки збіжності невласних інтегралів 1-го роду.
В тих випадках, коли потрібно встановити збіжність чи розбіжність невласного інтеграла, не обчислюючи його значення, зручно користуватися ознаками збіжності, які наведені у наступних теоремах.
Теорема
1.
(ознака порівняння). Нехай
для будь-яких
 виконується нерівність
виконується нерівність
 ,
тоді
,
тоді
1) Якщо
інтеграл
 збігається, то збігається й інтеграл
збігається, то збігається й інтеграл
 .
.
2) Якщо інтеграл розбігається, то розбігається й інтеграл .
Теорема
2.
(гранична
ознака порівняння).
Нехай функції
і
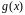 неперервні і додатні на проміжку
.
Тоді, якщо існує скінчена границя
неперервні і додатні на проміжку
.
Тоді, якщо існує скінчена границя
 ,
то інтеграли
і
,
то інтеграли
і
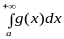 або водночас обидва збігаються або
водночас розбігаються.
або водночас обидва збігаються або
водночас розбігаються.
В теоремах 1 і 2 функція називається функцією порівняння. За таку функцію береться функція, відносно якої нам відома поведінка невласних інтегралів від них. Наприклад, такими є
1) функція
вигляду
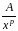 ,
де
,
де
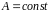 .
.
Якщо
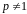 ,
то
,
то
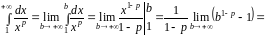
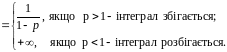
2)


3)
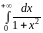 – збігається.
– збігається.
В теоремах 1 і 2 розглядалися невласні інтеграли від функцій, які зберігали свій знак на проміжку інтегрування, коли ж підінтегральна функція є знакозмінною, то має місце теорема.
Теорема
3.
(про абсолютну збіжність). Якщо
інтеграл
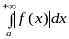 збігається, то збігається й інтеграл
.
збігається, то збігається й інтеграл
.
Визначення. Невласний інтеграл називається абсолютно збіжним якщо збігається інтеграл , і умовно збіжним, якщо інтеграл розбігається , а інтеграл збігається.
Теорема 4. (про порівняння). Нехай функції і неперервні на проміжку . Тоді:
якщо принаймні для достатньо великих значень , виконується нерівність
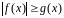 ,
то із збіжності інтеграла
випливає абсолютна збіжність інтеграла
.
,
то із збіжності інтеграла
випливає абсолютна збіжність інтеграла
.
якщо принаймні для достатньо великих значень , виконується нерівність
 ,
то із розбіжності інтеграла
,
то із розбіжності інтеграла
 випливає розбіжність інтеграла
.
випливає розбіжність інтеграла
.
Зауваження.
Для дослідження збіжності інтеграла
 треба дослідити збіжність кожного з
інтегралів
треба дослідити збіжність кожного з
інтегралів
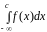 і
і
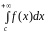 .
Якщо обидва інтеграли збігаються, то і
початковий інтеграл буде збіжним, якщо
ж хоча б один з них розбігається, то і
початковий інтеграл буде розбіжним.
.
Якщо обидва інтеграли збігаються, то і
початковий інтеграл буде збіжним, якщо
ж хоча б один з них розбігається, то і
початковий інтеграл буде розбіжним.
