Домашняя работа №1. Динамика материальной точки. Вариант - 10. (2 семестр)

Московский Государственный Университет Инженерной Экологии

Кафедра «Теоретическая механика»

Тема: «Динамика материальной точки»

Вариант – 10.

Работу выполнил: Рузанов Леонид

Студент группы: М - 23

Работу проверил: Серов Михаил Владимирович

2005 год.

Москва.

Точка массой m имеет начальную скорость V₀ и движется горизонтально прямолинейно в среде, сопротивление которой пропорционально квадратному корню из величины скорости, т.е. равна (k – величина постоянная).

По истечении какого времени точка будет находиться в покое?

Какой путь пройдёт точка до остановки?

Дано:

m;

V(0)=V₀;

R=

H-?

T-?

Решение:

1. Рассмотрим движение точки М.

2. Укажем оси координат.

Направим ось х по направлению движения.

3. Изобразим внешние силы:

а) заданные: нет;

б) реакций связей (среда): R.

4. Применим II закон Ньютона и составим общее уравнение движения точки:

(1)

5. Проецируем (1) на ось х:

; ; (2) с начальным условием V(0)=V₀ (3).

6. Определим путь, пройденный точкой до остановки (H):

Решим это равенство с условием (3):

Проинтегрируем полученное равенство:

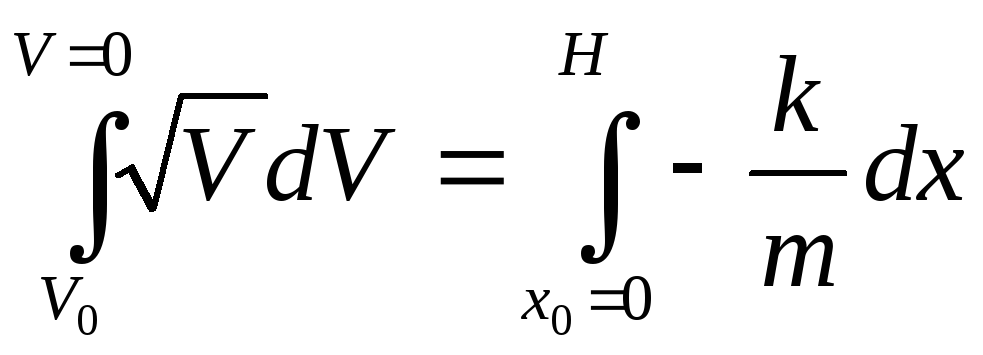, получим:

(4)

Из (3) => и тогда равенство (4) примет вид:

.

Подставив сюда V=0, находим пройденный путь до остановки:

.

7. Определим через какое время точка будет находиться в покое (T):

Решаем (2) методом разделения переменных:

(5)

Из условия (3) следует, что:

и тогда равенство (5) примет вид:

Подставив сюда V=0, находим время, через которое точка будет находиться в покое:

.

Ответ: ; .

3