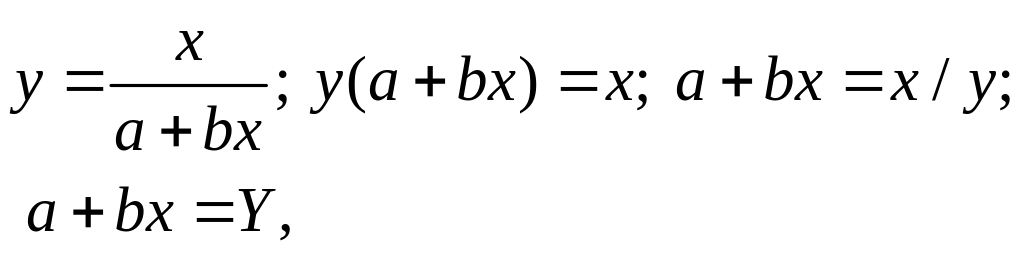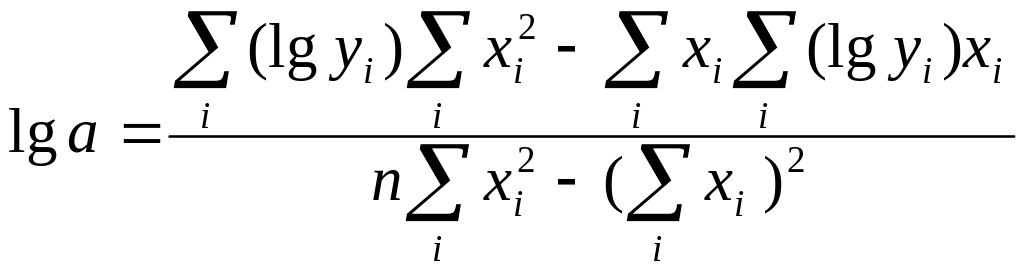6.2. Работа №2. Корреляционно-регрессионный анализ параметров

транспортного процесса

Бланк задания приведен ниже

Задание №2

Тема: «Корреляционно-регрессионный анализ параметров

транспортного процесса»

Постановка задачи. В результате наблюдений зафиксированы нижеприведённые значения_________________________________

в зависимости от______________________________________

По приведенным данным необходимо установить:

– тесноту связи между указанными параметрами;

– вид уравнения регрессии;

– численное значение коэффициентов уравнения регрессии;

– отразить на графике статистическую и теоретическую кривые;

– относительную ошибку.

Исходные данные:

Значение параметра 1, ______
Значение параметра 2, ______

Методика выполнения задания

Окружающий нас мир развивается на основе диалектики, основанным принципом которой является всеобщая связь. В эксплуатационной практике всеобщая связь наблюдается повсюду. Так с ростом валовой производительности работы флота (Р_в) снижается себестоимость перевозок (S), ростом эксплуатационной загрузки теплохода (Q_э) увеличиваются затраты ходового времени (t_х) и т.д. Связь между этими параметрами может быть сильной, слабой, а в отдельных случаях отсутствовать. Например, между мощностью теплохода и коэффициентом вертикальной проницаемости его трюмов связь отсутствует.

Определение тесноты связи

Когда наблюдается строгая зависимость между параметрами (например, цена кг капусты и стоимость покупки), то говорят о строгой функциональной зависимости. Она может быть прямой (больше кг – больше стоимость покупки) и обратной (больше цена – меньше кг). В эксплуатационной практике строгие функциональные зависимости наблюдаются редко, однако с ростом Р_в – снижается S. В подобных случаях говорят о корреляционной (с латинского – взаимное отношение предметов) связи двух величин х и у, где х – варьируемый (изменяющийся) параметр Р_в, а у – результирующие значение параметра S, связанное с изменением х (Р_в).

Если между исследуемыми параметрами есть функциональная зависимость, и она является сильной, представляется целесообразным установить закономерность, в соответствии с которой она развивается. При этом закономерность может быть самой разной.

В практических расчетах для упрощения зачастую предполагают наличие линейной зависимости между параметрами х и у. Тогда теснота связи между ними определяется численным значением коэффициента линейной корреляции

(60)

где n – статистическое число наблюдаемых пар параметров; i – признак пары; x_i и y_i – статистические значения исследуемых параметров.

Следует отметить, что х и у имеют размерности физических величин, рассматриваемых в каждом конкретном случае.

Численное значение коэффициента корреляции изменяется в пределах 0 ≤ r_y,x ≤ ± 1. Если r_y,x →0, то это свидетельствует об отсутствии связи между параметрами х и у, при r_y,x→1 наблюдается практически строгая функциональная зависимость, прямая – при положительном значении и обратная в противном случае. В практических расчетах при r_y,x ≥ ± 0,4 предполагают наличие тесной связи.

По результатам расчета r_y,x делается вывод о тесноте и направлении связи.

Определение вида теоретического уравнения

При наличии тесной связи исследуемых параметров возникает важная практическая задача о выборе теоретического уравнения у = f(x), наличие которого позволяет определить значение параметра у при любых возможных значениях х (например, показатель себестоимости перевозок грузов на основе данных оперативного учета использования флота по валовой производительности). Такое уравнение, полученное на основе исследования опытных (статистических) данных, называют уравнением регрессии (с латинского – движение в обратную сторону. Здесь следует понимать как движение от теории к статистике).

Как правило, при любом исследовании вид уравнения регрессии заранее неизвестен, поэтому определяется эмпирическая (опытная) формула ,значения которой при в наибольшей мере соответствовали бы статистическим данным у_i. В качестве исходного можно исследовать уравнение вида

(61)

Однако использование этого уравнения вызывает довольно значительные затруднения при определении численных значений коэффициентов а, b,... . С целью исключения этих затруднений рекомендуется использовать приведенные в табл. 6 довольно простые, апробированные в практике исследований, эмпирические формулы, которые позволяют с достаточной степенью сходимости аппроксимировать разнообразные зависимости.

Таблица 6

Эмпирические формулы для аппроксимации

эксплутационно-экономических зависимостей

Вид эмпирической формулы	Способы определения и
Линейная зависимость	Среднеарифметическое значение
Обратно-пропорциональная зависимость	Среднеарифметическое значение	Среднегармоническое значение
Степенная зависимость	Среднегеометрическое значение
Показательная зависимость	Среднегеометрическое значение	Среднеарифметическое значение
Гиперболическая зависимость	Среднегармоническое значение	Среднеарифметическое значение
Дробно-линейная зависимость	Среднегармоническое значение
Логарифмическая зависимость	Среднеарифметическое значение	Среднегеометрическое значение

Примечание. В табл.6 в качестве у₁(х₁) и у_n(x_n) принимаются соответственное первое и последнее значения из статистического ряда.

При обосновании вида уравнения регрессии используется вариантная методика и рекомендуется следующая последовательность действий.

1. Используя статистический ряд у_i , х_i определяют в соответствии с формулами табл. 6 значения и и результаты расчетов сводятся в табл. 7, форма которой приведена ниже.

Таблица 7

Выбор вида уравнения регрессии

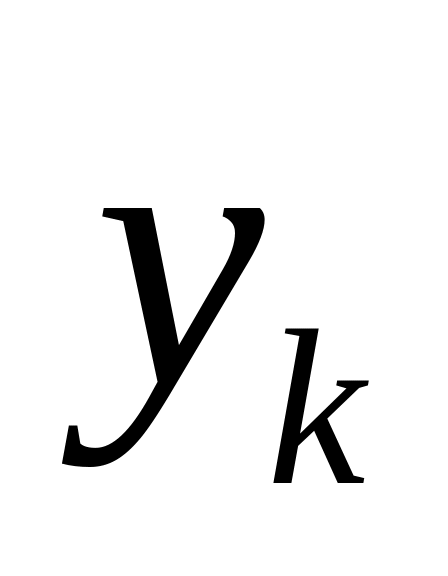
Модуль

В графах табл. 7 , указываются не только конечные значения, но и исходные для расчета числа.

2. Мы, в конечном счете, выбираем функцию, которая бы максимально точно аппроксимировала исследуемый статистический ряд. Однако практика исследований показывает, что крайне редко значение соответствует одному из статистических у_i, а попадает в некий интервал i и i+1. В этом случае рекомендуется использовать способ линейной интерполяции

(62)

Ориентиром для выбора границ интервалов i и i+1 в статистическом ряду является значение .

3. Уравнением регрессии будет то, которое обеспечивает min , т.е. минимальное расхождение между статистическим и теоретическим (эмпирическим) распределениями.

Выбранное уравнение регрессии указывается в выводе в исследуемых согласно заданию физических величинах.

Определение численных значений коэффициентов уравнения регрессии

Мы рассматриваем относительно простые эмпирические формулы, в которых только два коэффициента – а и b. Для определения их значений используется ряд методов, из которых наиболее часто применяются методы наименьших квадратов и средних.

Метод наименьших квадратов

Требует минимального значения суммы квадратов отклонений между теоретическими и статическими значениями распределений

(63)

В соответствии с методом наименьших квадратов значения коэффициентов регрессии находятся из решения системы двух уравнений

(64)

Таким образом, значения коэффициентов a и b определяются по формулам

,	(65)
.	(66)

Формулы (64), (65) и (66) справедливы только для линейной (нормальной) зависимости. Для других зависимостей используется прием линиаризаций, т.е. формальное приведение их к виду уравнения прямой линии заменой переменных.

Обратно-пропорциональная зависимость

	(67)
где

Степенная зависимость

	(68)
где

Показательная зависимость

	(69)
где

Гиперболическая зависимость

	(70)
где

Дробно-линейная зависимость

	(71)
где Y = x / y.

Логарифмическая зависимость

	(72)
где .

Основываясь на вышеизложенном, система уравнений и выражения для определения коэффициентов a и b применительно, например, к показательной зависимости будут иметь вид

,

(73)

,

(74)

(75)

(76)

Указание. При расчетах, по вышеприведенным формулам точность в пределах 2–3 знаков после запятой является вполне приемлемой. А применительно к гиперболической и дробно-линейной зависимостям, точность должна быть на уровне 6–7 знаков.

При выполнении конкретного задания студент, применительно к исходным данным, определяет вид уравнения регрессии, выполняет линиаризацию и указывает систему уравнений применительно только к своей зависимости, разрешает систему уравнений и приводит свое уравнение регрессии с численными значениями коэффициентов, например (пример носит условный характер)

где a = 1,75, b = 8,67.

Метод средних требует нулевых отклонений между статическим и теоретическим распределениями и формирование системы линиализированных (нормальных) уравнений по числу имеющихся наблюдений вида

(77)

Тогда, например, при n = 4 и показательной зависимости эта система уравнений будет иметь вид

(78)

Нетрудно заметить что систему (78) можно решить путем приведения ее к системе двух уравнений почленным сложением отдельно первого и второго, а так же третьего и четвертого уравнений. Система двух уравнений решается методом вычитания, что позволяет получить значение коэффициента b. Коэффициент a определяется из любого уравнения системы (78).

Таким образом, мы имеем два уравнения регрессии, значения коэффициентов которых получены разными методами, и, следовательно, обладают разной степенью адекватности исследуемому явлению.

Выбор адекватного уравнения регрессии производится на базе информации по форме табл. 8.

В табл. 8, под х и у подразумеваются конкретные физические величины из задания.

Размер отклонений определяется по формуле

(79)

Таблица 8

Выбор адекватного уравнения регрессии

Статистическое значении x	Статистическое значение y	Теоретическое значение y
		Метод наименьших квадратов	Отклонения, %	Метод средних	Отклонения, %

Адекватным уравнением регрессии будет то, для которого алгебраическая сумма отклонений будет минимальна.

На базе информации табл. 8 строится графическая зависимость исследуемого явления на листе миллиметровки формата А4. Здесь указываются дискретные точки статического распределения, которые соединяются отрезками прямой линии, а так же точки адекватного уравнения регрессии, которые соединяются плавной кривой. Именно эта теоретическая графическая зависимость позволяет в дальнейшей практической деятельности определить значение у при любых возможных значениях х.