6.4. Контрольные вопросы

1. Составьте схему расчета диска произвольного профиля.

2. Основные допущения расчетной схемы.

3. Назовите нагрузки, действующие на диски компрессоров и газовых турбин.

4. Почему при расчете прочности дисков газовых турбин необходимо учитывать температуру и её изменение по радиусу?

5. Какие напряжения возникают во вращающемся нагретом диске?

6. Каким образом влияет профиль диска на распределения напряжений?

7. Какой диск называется равнопрочным?

8. Обоснуйте влияние на напряжения в диске контурной нагрузке от лопаток.

9. Как изменяются напряжения в диске при выполнении в нем центрального отверстия?

10. Как влияет величина натяга при запрессовке диска на вал?

11.Обоснуйте необходимость при определении напряжений учитывать материал дисков?

12. Диск, какой формы имеет минимальную массу и почему?

7. Колебания дисков

Диски роторов являются одними из наи­более нагруженных элементов авиадвигателей. При работе в них возникают напряжения от центробежных и осевых сил, температурные на­пряжения, напряжения от газодинамических сил и т.д. Эти нагрузки зачастую переменны, что вызывает колебания дисков, а при опреде­ленных частотах и амплитудах ведут к их разрушению, в итоге все это приводит к катастрофическим последствиям.

Формы колебаний дисков (рис.7.1) могут быть: без узловых линий ( ) - зонтичные; с узловыми диаметрами - волнообразные («веерные») (s=0; i=2,3,4 и т.д.); с узловыми окружностями - «осесимметричные» (i=0; s=0,1,2,3 и т.д.); комбинация узловых окружностей и диаметров ( ).

Каждой форме колебаний соответствует своя частота. Чем больше число узлов колебаний, тем выше частота колебаний.

Наиболее опасными являются «веерные» колебания с двумя и более диаметрами.

Рис.7.1. Формы колебаний дисков: - число узловых диаметров; - число узловых окружностей; 1 – узловые диаметры; 2 – узловые окружности

Волнообразные колебания невращающихся дисков

Рассмотрим волнообразные колебания диска с числом узловых диаметров равным двум (рис.7.2).

Рис.7.2. Схема веерных колебаний с двумя узловыми диаметрами

Уравнения прогибов точек диска при колебаниях в полярной системе координат запишется

(7.1)

где - функция радиуса, определяющая форму колебаний диска по радиусу; - полярный угол, отсчитываемый от одного из узловых диаметров; - круговая частота свободных колебаний диска; - время.

Перемещение точек, лежащих на радиусе рис.7.2 в момент времени подчиняется гармоническому закону.

Каждой форме собственных колебаний соответствует строго определенная частота колебаний. Для простых круглых пластин частота может быть подсчитана по формуле

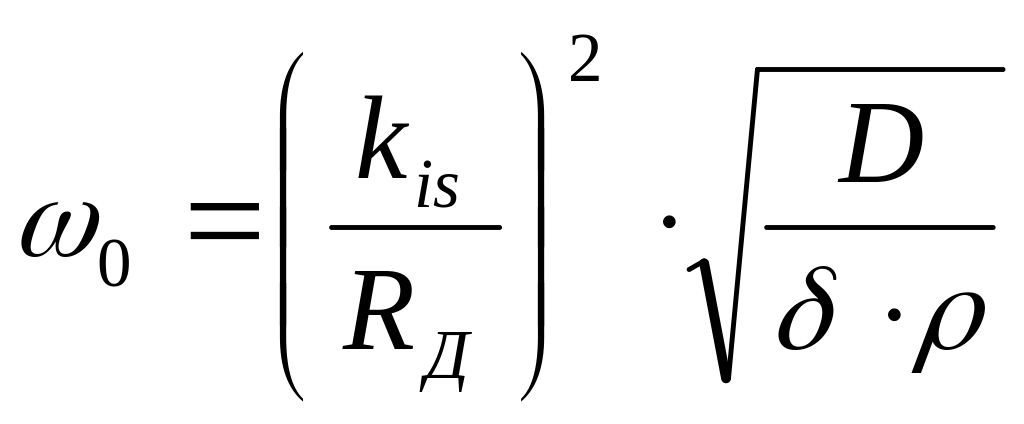(7.2)

где ρ - массовая плотность материала диска; δ- толщина диска; - наружный радиус диска; μ- коэффициент Пуассона;

- цилиндрическая жесткость;

- коэффициент частоты, определяемый формой колебаний и условиями закрепления.

В таблицах 7.1 и 7.2 приведены значения коэффициентов частоты для условий закрепления пластины по внешнему и внутреннему диаметрам.

Закрепление пластины на внешнем диаметре таблица 7.1

число узловых окружностей	число узловых диаметров
	i=0	i=1	i=2	i=3
s=0	10,24	21,25	33,60	51
s=1	39,80	60,80	84,60	111
s=2	89,00	120	153,8	190
s=3	158,30	199	243	-

Закрепление пластины по центральному отверстию таблица7.2

число узловых окружностей	число узловых диаметров
	i=0	i=1	i=2	i=3
s=0	3,75	3,42	5,39	12,49
s=1	20,91	27,56	34,80	53,30
s=2	60,68	-	-	-

Формула (7.2) и таблицы коэффициентов позволяют проанализировать соотношения собственных частот различных форм колебаний и зависимость от основных размеров, материала и условий закрепления.

Формы собственных колебаний рабочих колес компрессоров и газовых турбин ГТД аналогичны формам колебаний простых пластин с учетом реальных факторов.

Представим произведение косинусов (7.1) в виде суммы

(7.3)

тогда

(7.4)

Каждое слагаемое формулы (7.4) представляет собой колебание точек диска, сдвинутые по фазе на угол, пропорциональный координате . Колебания имеют вид фазовых волн - первое слагаемое волны с числом узловых диаметров , бегущую по диску в круговом направлении в сторону отсчета углов , а второе слагаемое – волну, бегущую навстречу (рис. 7.3).

Рис. 7.3. Расположение бегущих на

диске волн: а- волна в сторону

вращения; б – волна во встречном

направлении

Каждое из слагаемых по отдельности удовлетворяет общему уравнению колебаний диска, поэтому их можно рассматривать как независимые решения. То есть фазовые волны могут существовать на диске независимо друг от друга.

Для любого узлового диаметра выполняется условие При этом условии должно выполняться равенство

(7.5)

где - угол, определяющий место расположения узлового диаметра рис. 7.3.

(7.6)

знак плюс относится к волне, бегущей вперед, а знак минус - к волне, бегущей навстречу. Из формулы видно, что угол расположения узловых диаметров с течением времени меняется.

Продифференцируем выражение (7.6), получим скорость перемещения узловых диаметров по диску

(7.7)

Волны бегут в противоположные стороны с одинаковой скоростью, пропорциональной частоте собственных колебаний.

Правило движения фазовых волн сохраняется и на вращающемся с угловой скоростью диске. С учетом увеличения собственных частот вследствие вращения диска, абсолютные скорости фазовых волн относительно неподвижной системы координат, определяются

. (7.8)

Из (7.8) очевидно, что абсолютные угловые скорости прямых и обратных и волн различны.

Абсолютная угловая скорость обратной волны уменьшается с ростом угловой скорости вращения диска и при становится равной нулю. При этом сама форма колебаний относительно неподвижных осей оказывается неподвижной, а все точки вращающегося диска, следуя по этой форме, совершают поперечные колебания.

Угловые скорости вращения, при которых форма колебаний остается неподвижной относительно неподвижной системы координат называется критической и определяется

. (7.9)

На критических скоростях вращения возникает явление резонанса, диск теряет устойчивость. Под воздействием неосесимметричного статического давления на боковую поверхность диска или лопатки появляются большие деформации и напряжения изгиба диска, что может привести к задеванию о статор, обрыву лопаток и разрушению диска.

Для исключения опасных резонансных явлений в зоне рабочих угловых скоростей вращения роторов не рекомендуется допускать существования критических угловых скоростей дисков, особенно с числом узловых диаметров Для определения критических угловых скоростей необходимо знать собственные частоты колебаний диска как функции угловой скорости.

Для определения опасных оборотов на графике строятся зависимости собственных частот от угловых скоростей вращения ротора и из начала координат проводятся прямые . Точки пересечения прямых определяют критические угловые скорости вращения дисков (рис.7.4).

Рис.7.4. Определение критических

скоростей вращения рабочих колес

Рекомендуется на двигателях иметь запас по критическим скоростям вращения

(7.10)

В зависимости от числа узловых диаметров

Отстроиться от резонансных режимов можно изменением собственной частоты колебаний дисков или изменением порядка гармоник возмущающих сил.

Проведем анализ влияния различных факторов на собственные частоты.

Собственные частоты колебаний диска повышаются до 1.5…2 раз с увеличение коничности или гиперболичности полотна диска. Широкий обод на периферии диска увеличивает его изгибную жесткость, что может увеличить частоту собственных колебаний на 10…15%.

Лопатки, расположенные на периферии диска снижают собственные частоты колебаний дисков. Причем снижение частот определяется как соотношением масс лопаток и массы диска , так и соотношением длинны лопатки и радиуса диска. Типовые зависимости собственных частот колебаний рабочих колес с учетом этих факторов приведены на рис.7.5.

Рис.7.5. Влияние массы

лопаток на частоту собственных

колебаний рабочих колес

Существенное влияние на частоты собственных колебаний оказывает угловая скорость вращения рабочего колеса так как центробежные силы от масс диска стремятся вернуть отклоняющиеся части диска в состояние равновесия, что приводит к увеличению частоты собственных колебаний (рис.7.6). Повышение частот собственных колебаний рабочих колес от угловой скорости вращения ротора зависит от геометрической формы рабочего колеса и лопаток, соотношения их масс и жесткостей и может достигать двукратного значения. Расчет собственных частот колебаний рабочих колес производится по энергетическому методу Рэлея. Количественная зависимость может быть представлена формулой

(7.11)

где - коэффициент влияния угловой скорости.

Температура дисков влияет на собственные частоты колебаний за счет изменения модуля упругости материала. Кроме этого при рабочих режимах температура дисков существенно изменяется по радиусу, что приводит к возникновению больших напряжений сжатия на периферии и напряжений растяжения в центре. При этом частоты собственных колебаний рабочих колес снижаются, что может быть определено по методу Рэлея.

Рис.7.6.Влияние скорости вращения

на частоту собственных колебаний

диска

Расчет собственной частоты колебаний диска с лопатками с учетом изменения температуры для формы колебаний с двумя узловыми диаметрами можно оценить по формуле

(7.12)

где - коэффициент линейного температурного расширения материала диска; - средняя ширина диска; - модули упругости материала на среднем диаметре при температуре t и ; - разность температур на внешнем контуре и центре диска.

Закон изменения температуры по радиусу диска принят кубическим

При этом снижение частот собственных колебаний, может происходить на 20…25%, увеличиваясь для тонких дисков большого диаметра.

В реальном двигателе на диск одновременно воздействует угловая скорость и температура, поэтому при малых угловых скоростях основное влияние оказывают центробежные силы лопаток, а с ростом скорости вращения ротора и температуры – температурный фактор. Поэтому для одних форм колебаний происходит увеличение собственных частот колебаний для других снижение (рис. 7.7).

Рис.7.7. Влияние скорости вращения

и температуры на частоту собственных колебаний диска

Таким образом, приведенные зависимости позволяют проводить расчеты частот и форм собственных колебаний дисков с учетом влияния реальных факторов.

Форма и частота колебаний зависят не только от конструкции ротора ГТД, но и от режима эксплуатации. Амплитуды колебаний дисков при резонансных режимах могут быть значительными, поэтому работа двигателей на резонансных режимах недопустима.