
- •1.1 Расчет напряжений растяжения………………….. …..…8
- •1.2 Расчёт изгибающих моментов………………...……… ...13
- •4. Крутильные колебания роторов гтд………...………………..90
- •8.3.2. Планетарные редукторы………………………………..….138
- •8.5.1 Зубчатые цилиндрические и конические колеса……......…146
- •8.6. Измерители крутящего момента……......…..….…....156
- •9.1.1. Конструкция нерегулируемых дозвуковых выходных устройств………………………………………………………………...….......172
- •Введение
- •1. Расчёт лопаток компрессоров и турбин на прочность
- •1.1 Расчет напряжений растяжения
- •1.2 Расчёт изгибающих моментов
- •1.2.1 Определение изгибающих моментов от действия центробежных сил
- •1.2.2 Определение изгибающих моментов от центробежных сил методом конечных разностей
- •1..2.3. Расчёт изгибающих моментов в лопатках от действия газовых сил
- •1.3. Определение напряжений изгиба, суммарных напряжений и запасов прочности
- •1.4. Расчет на прочность замков крепления рабочих лопаток
- •1.4.1. Расчёт крепления лопатки типа «ласточкин хвост»
- •1.4.2 Расчёт крепления лопатки замком типа «ёлочка»
- •1.5. Контрольные вопросы
- •2. Колебание лопаток
- •2.1 Свободные колебания стержня постоянного поперечного сечения
- •2.2. Расчет первой собственной частоты колебаний лопатки переменного сечения
- •2.3. Определение частоты колебания лопатки в поле центробежных сил
- •2.4. Резонансные режимы и способы борьбы с опасными колебаниями
- •2.5 Контрольные вопросы
- •3. Критические скорости вращения роторов
- •3.1. Расчет критической скорости вращения невесомого вала с диском
- •3.2 Устойчивость быстровращающихся гладких валов
- •3.3. Критические скорости вращения реальных роторов
- •3.4. Влияние гироскопического момента на критические скорости вращеня
- •3.4.1 Расчет критической скорости вращения ротора с учётом гироскопического момента
- •3.5. Расчет крических скоростей вращения многодисковых роторов
- •3.6. Приведение сложных изгибных систем к эквивалентным
- •3.7. Контрольные вопросы
- •4. Крутильные колебания роторов гтд
- •4.1. Свободные крутильные колебания двухмассовой системы
- •4.2. Свободные крутильные колебания многомассовых систем
- •4.3. Приведение реальной крутильной системы к эквивалентной расчетной
- •4.4. Вынуждающие моменты и резонанс
- •4.5. Контрольные вопросы
- •5.Вибрационные перегрузки двигателей
- •5.1. Балансировка роторов гтд
- •5.2. Контрольные вопросы
- •6. Расчёт на прочность дисков роторов гтд
- •6.2 Расчет равнопрочного диска
- •6.3. Расчет на прочность вращающегося диска произвольного профиля
- •6.4. Контрольные вопросы
- •7. Колебания дисков
- •7.1 Контрольные вопросы
- •8. Редукторы гтд
- •8.1. Требование к редукторам
- •8.2. Классификация редукторов
- •8.3. Редукторы для привода одиночного винта
- •8.3.1 Простые редукторы
- •8.3.2. Планетарные редукторы
- •8.3.3. Двухступенчатые редукторы для привода одиночного винта
- •8.3.4. Замкнутые дифференциальные редукторы для привода одиночного винта
- •8.4. Редукторы для привода двух соосных винтов
- •8.5. Конструкция редукторов гтд
- •8.5.1 Зубчатые цилиндрические и конические колеса
- •8.5.2. Водила планетарных передач
- •8.5.3. Корпусы редукторов
- •8.5.4. Валы и их опоры
- •8.5.5. Применяемые материалы
- •8.6. Измерители крутящего момента
- •Контрольные вопросы
- •9. Выходные и ревеверсивные устройства
- •9.1.1. Конструкция нерегулируемых дозвуковых выходных устройств
- •9.3. Сверзвуковые регулируемые выходные устройства
- •9.4. Устройства для реверса и девиации тяги
- •9.5. Методы снижения шума
- •9.5.1 Шумоглушащие сопла
- •9.5.2 Снижение шума компрессора
- •9.5.3 Аэродромные глушители шума
- •Глушители шума выхлопа двигателя
- •Глушители шума на входе в двигатель
- •9.6. Контрольные вопросы
- •Заключение
- •Библиографический список
- •660014, Г. Красноярск, просп. Им. Газ. «Красноярский рабочий»,31
- •660028 Г. Красноярск . Ул. Л Кецховели, 75а-223.
3.7. Контрольные вопросы
1. Приведите факторы, вызывающие колебания роторов.
2. Какая скорость вращения ротора называется критической?
3. Дайте определение жесткости системы.
4. Чем отличается динамическая жесткость от статической.
5. Зачем при расчете критических скоростей необходимо рассматривать сложные системы « ротор - корпус»?
6.Назовите факторы, влияющие на критические скорости вращения роторов.
7. Почему работа роторов на критических скоростях вращения недопустима?
8. Способы борьбы с опасными колебаниями роторов двигателей.
9. Как рассчитать критическую скорость многодискового ротора.
10. Объясните влияние гироскопического момента на критические скорости вращения роторов.
4. Крутильные колебания роторов гтд
Элементы
ротора ГТД: диски компрессоров, газовых
турбин, шестерни редукторов, воздушные
винты и т.д., соединенные валами образуют
упругую систему, которая под действием
изменяющегося крутящего момента может
совершать крутильные колебания
(колебания в окружном направлении). При
крутильных колебаниях массы системы
находящиеся во вращательном движении
поворачиваются относительно друг друга
на угол
![]() (рис.4.1), вызывая на валу и других упругих
элементах ротора напряжения кручения,
которые могут быть причиной усталостного
излома.
(рис.4.1), вызывая на валу и других упругих
элементах ротора напряжения кручения,
которые могут быть причиной усталостного
излома.

Рис.4.1. Схема турбовинтового двигателя с моментами инерции
Источником крутильных колебаний в ГТД являются газовые и инерционные силы, а в ТВД ещё и воздушный винт и редуктор.
4.1. Свободные крутильные колебания двухмассовой системы
Рассмотрим
расчётную схему системы состоящей из
двух дисков с моментами инерции
![]() ,
соединенных упругим валом, установленным
в двух опорах (рис.4.2). Вал одного диаметра
а, следовательно, и с постоянной
крутильной жёсткостью
,
соединенных упругим валом, установленным
в двух опорах (рис.4.2). Вал одного диаметра
а, следовательно, и с постоянной
крутильной жёсткостью
![]() .
.

Рис.4.2. Расчетная схема ротора с двумя дисками
Приложим
к системе крутящий момент
![]() и, закрутим вал на угол
.
После мгновенного снятия нагрузки
система будет совершать крутильные
колебания за счет сил инерции и упругости
вала.
и, закрутим вал на угол
.
После мгновенного снятия нагрузки
система будет совершать крутильные
колебания за счет сил инерции и упругости
вала.
Отклонение сосредоточенных масс относительно положения равновесия происходит в разные стороны, поэтому на валу имеется сечение, которое остаётся неподвижным. Это сечение (точка О на рис.4.2.) называется узлом колебаний.
При различных диски имеют одинаковую частоту колебаний и различные амплитуды.
Так как узел колебаний остается неподвижным, то можем считать его заделкой вала и перейти от двухмассовой системы к двум одномассовым системам с одинаковой частотой колебаний (рис.4.2),
которую можно рассчитать по зависимости
![]() (4.1)
(4.1)
Жёсткости участков вала равны
![]() ;
;
![]() (4.2)
(4.2)
где - полярный момент инерции сечения вала, постоянный по длине; G- модуль сдвига.
Подставим (4.2) в тождество (4.1), получим
![]() (4.3)
(4.3)
так
как
![]() ,
то
,
то
![]()
![]() (4.4)
(4.4)
Частота крутильных колебаний равна
![]() (4.5)
(4.5)
Подставим в (4.5) выражение для
![]() (4.6)
(4.6)
где
![]() -
жесткость всего вала.
-
жесткость всего вала.
Уравнения
колебаний двух одномассовых систем
(рис. 4.2), при отсутствии сил сопротивления,
определяется значениями углов закрутки
![]() :
:
![]() (4.7)
(4.7)
Амплитуды
колебаний
![]() равны
углам закрутки масс дисков под действием
статического крутящего момента
равны
углам закрутки масс дисков под действием
статического крутящего момента
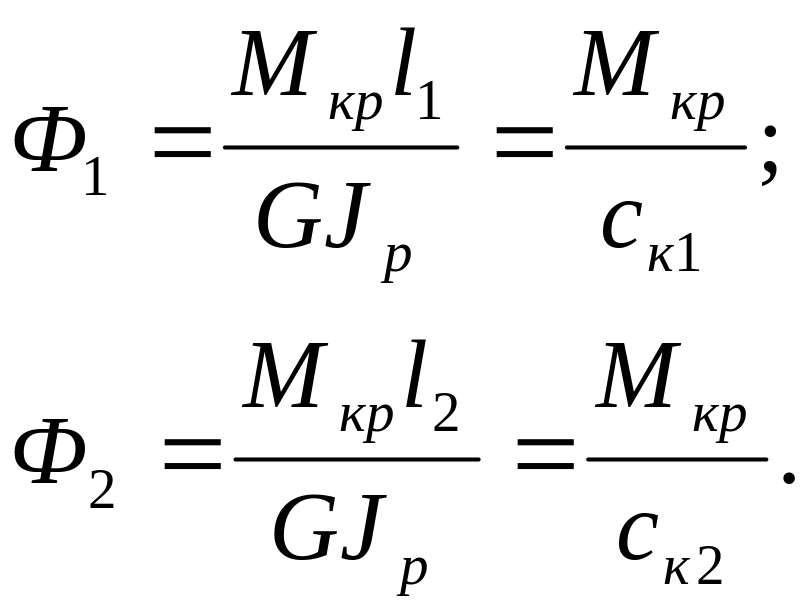 (4.8)
(4.8)
Амплитуды прямо пропорциональны расстояния до узла колебаний и обратно пропорциональны моментам инерции колеблющихся масс
![]() (4.9)
(4.9)
Знак минус означает, что массы колеблются в разные стороны.
