49) .Залежність ккд передачі від ступеня її навантаження.

Существуют методы расчета КПД при частичной загрузке аналитическим путем, однако для этого требуются дополнительные исходные данные о распределении величин постоянных и переменных потерь в функции номинального КПД Потери в передачах имеют две составляющие: 1) постоянные потери (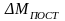 ), зависящие от конструкции опор передаточного устройства, от вязкости смазки, качества зубцов и износа их, а также от величины скорости. 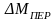Зависимость ΔМ_ПОСТ=f(ω) незначительна и мало исследована, поэтому она не учитывается; 2) переменные потери , зависящие от величины нагрузки. КПД передачи может быть выражен следующим образом:

.

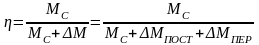
Обозначим коэффициенты постоянных а и переменных b потерь в передачах как ; , что позволяет выразить КПД передачи так:

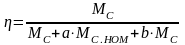
Разделим на М_С и учтем, что . Тогда . Расчет

КПД при частичной загрузке

можно вести по последней формуле.

Однако лучше ввести в расчет величину номинального КПД η_Н, от которого зависят коэффициенты потерь а и b:

; ;

; .

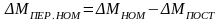
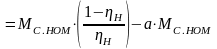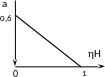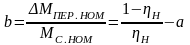Значение а=f(η_Н), необходимое для пользования формой по подсчету η=f(К_З), берется из графика а=f(η_Н), показанного на рисунке.

50) Виведення рівняння руху першої маси тримасової динамічної системи з допомогою узагальненого рівняння Лагранжа.

L=W_k-W_n - функция Лагранжа, равная разности запасов кинетической W_k и потенциальной энергии W_n.

Запас кинетической энергии в системе:

Запас потенциальной энергии деформации упругих элементов, подвергающихся скручиванию:

Здесь М₁₂ и М₂₃ – моменты упругого взаимодействия между инерционными массами J₁ и J₂, J₂ и J₃, зависящие от величины деформации ₁-₂ и ₂-₃.

На инерционную массу J₁ действуют моменты М и М_с1. Элементарная работа приложенных к J₁ моментов на возможном перемещении _₁:

Следовательно, обобщенная сила .

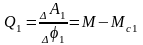Аналогично элементарная работа всех приложений ко 2-й и 3-й массам моментам на возможных перемещениях _₂ и _₃: , откуда ; , откуда

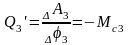
т.к. ко 2-й и 3-й массам электромагнитный момент двигателя не приложен. Функция Лагранжа L=W_k-W_n.

Учитывая значения Q1`,Q2`и Q3` и подставив их в уравнение Лагранжа, получим уравнения движения первой массы:

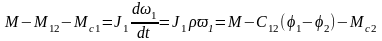
51).Виведення рівняння руху другої маси тримасової динамічної системи з допомогою узагальненого рівняння Лагранжа.

Механическая часть эл.привода представляет собой систему твердых тел, движущихся с различными скоростями. Уравнение движения ее можно определить на основе анализа запасов энергии в системе двигатель – рабочая машина, или на основе анализа второго закона Ньютона. Но наиболее общей формой записи диф. уравнений, определяющих движение системы, является уравнение Лагранжа (при наличии в системе потенциальных сил):

, где L=W_k-W_n функция Лагранжа, равная разности запасов кинетической W_k и потенциальной энергии W_n, – обобщенная скорость; q_i – обобщенный путь; Q_i – обобщенная сила, определенная суммой элементарных работ A_i всех действующих сил на возможных перемещениях qi: . В трехмассовой упругой системе за обобщенные координаты принимают угловое перемещение масс ₁,₂,₃ и соответствующие им угловые скорости ₁, ₂, ₃. .

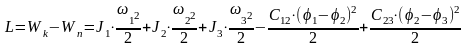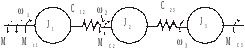
На инерционную массу J₂ действует момент М_с2. Элементарная работа приложенных к J₂ моментов на возможном перемещении _₂ , откуда .

Для второй массы . Следовательно уравнение Лагранжа запишется так