
- •36)Приведение к скорости двигателя момента инерции элемента кинематической схемы
- •37Приведение к скорости двигателя массы элемента поступательного движения.
- •3 8.Приведення до швидкостi двигуна жорсткостi пружного елемента обертального руху
- •39) Приведення до швидкості двигуна жорсткості пружного елемента поступального руху.
- •40. Приведення до швидкості двигуна моменту опору в елементі обертального руху.
- •41)Приведение к скорости двигателя сил сопротивления в элементе поступательного движения
- •42) Получение трех массовой расчетной модели в результате приведения к скорости двигателя параметров кинематической схемы. Система уравнений
- •43) Одержання двомасової розрахункової динамічної моделі в результаті приведення до швидкості двигуна параметрів кінематичної схеми. Система рівнянь.
- •45) Урахування коефіцієнта корисної дії передачі при приведенні до швидкості двигуна моменту опору механізму при прямому напрямку енергії.
- •46).Урахування коефіцієнта корисної дії передачі при приведенні до швидкості двигуна сили опору механізму при прямому напрямку енергії.
- •47)Учёт кпд передачи при приведении к скорости двигателя момента сопротивления механизма при обратном направлении энергии
- •48) Учет коэффициента полезного действия передачи при приведении к скорости двигателя силы сопротивления механизма при обратном направлении энергии.
- •49) .Залежність ккд передачі від ступеня її навантаження.
- •50) Виведення рівняння руху першої маси тримасової динамічної системи з допомогою узагальненого рівняння Лагранжа.
- •51).Виведення рівняння руху другої маси тримасової динамічної системи з допомогою узагальненого рівняння Лагранжа.
- •52)Выведение уравнения движения третьей массы трёхмассовой динамической системы с помощью обобщенного уравнения Лагранжа.
- •53) Вывод уравнения движения кривошипно-шатунной передачи.
45) Урахування коефіцієнта корисної дії передачі при приведенні до швидкості двигуна моменту опору механізму при прямому напрямку енергії.

46).Урахування коефіцієнта корисної дії передачі при приведенні до швидкості двигуна сили опору механізму при прямому напрямку енергії.
Чтобы решить задачу приведения, надо составить уравнение баланса кинетических энергий для реальной и эквивалентной систем, а также уравнение баланса мощности для этих систем, причем при составлении уравнения баланса мощности надо обязательно иметь в виду направление потока энергии, чтобы правильно учесть потери мощности в системе.
Уравнение
баланса
мощности,
если
поток
энергии
идет
от
двигателя
к
механизму
(т.е.
если
привод
работает
в
двигательном
режиме,
и
потери
в
передачах
покрываются
за
счет
мощности,
забираемой
двигателем
из
электрической
сети)
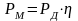 ,
или
;
,
или
;
Приведение МС и МСМ при двигательном режиме работы электропривода. В этом случае поток энергии из сети проходит через двигатель и передаточное устройство в рабочую машину. Уравнение баланса мощности: , где - общий КПД передаточного устройства.
В зависимости от постановки задачи и заданных исходных данных определяется либо статический момент, приведенный к валу двигателя МС, либо статический момент на валу механизма МСМ. При этом: ; ; . Итак, из уравнения можно найти ; .
47)Учёт кпд передачи при приведении к скорости двигателя момента сопротивления механизма при обратном направлении энергии
Суммарный приведённый статический момент Мс зависит от направления потока энергии. Для кинематической ветви с обратным направлением потока энергии, поступающей от рабочего органа:
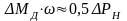
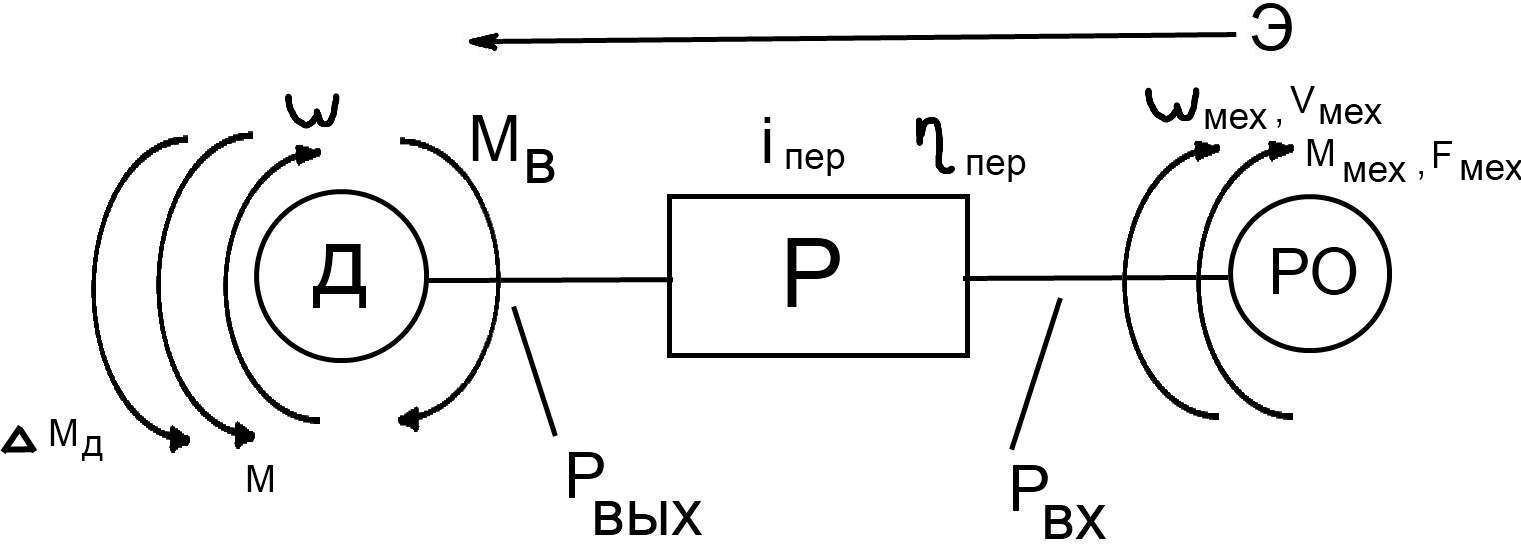
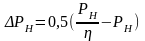
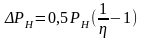
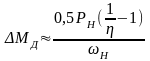
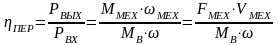 (1)
(1)
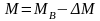 (2)
(2)
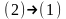
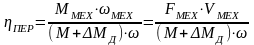 (3)
(3)
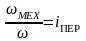 - передаточное
число
- передаточное
число
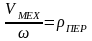 - радиус приведения
- радиус приведения
Из (3)
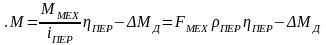
48) Учет коэффициента полезного действия передачи при приведении к скорости двигателя силы сопротивления механизма при обратном направлении энергии.
При вычислении
приведенного статического момента Мс
формулы (1.13) и (1.14) удобны для использования
в тех случаях, когда все действующие в
механизме силы и моменты определены.
Обычно потери на трение в механизме
неизвестны, и для их учета используется
КПД механизма мех=1·2·3….,
где 1,
2,
3
- КПД
элементов кинематической цепи. Е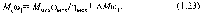 сли
известен полезный момент нагрузки
механизма Mмех,
то для прямого направления энергии
приведенный к валу двигателя момент
статической нагрузки может быть определен
из равенства
сли
известен полезный момент нагрузки
механизма Mмех,
то для прямого направления энергии
приведенный к валу двигателя момент
статической нагрузки может быть определен
из равенства
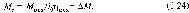 Следовательно,
Следовательно,
где M
- момент механических потерь в двигателе;
i0=1/мех=i1i2i3…-
общее передаточное число от двигателя
к рабочему органу механизма. При обратном
направлении потока энергии, когда
нагрузка является активной, движущей
и двигатель должен работать в тормозном
режиме, уравнение баланса мощностей с
помощью КПД передач можно записать так:
![]()
![]()
В этом случае
Момент механических потерь в двигателе невелик, составляет 1-5% номинального момента двигателя, причем большие значения его соответствуют двигателям небольшой мощности. Если значение M определить трудно, его можно ориентировочно оценить по этим данным. Во многих практических случаях в (1.24) и (1.26) полагают M=0, так как точность определения момента Mмех невелика, и он рассчитывается с некоторым запасом, при этом формулы приведения момента статической нагрузки к валу двигателя принимают вид:
д![]() ля
прямого направления передачи энергии
(двигательный режим работы двигателя)
ля
прямого направления передачи энергии
(двигательный режим работы двигателя)
д![]() ля
обратного (тормозной режим работы
двигателя)
ля
обратного (тормозной режим работы
двигателя)
![]() Если
рабочий орган движется поступательно,
уравнение баланса мощностей при прямом
направлении потока энергии, принимая
М=0,
можно записать так:
Если
рабочий орган движется поступательно,
уравнение баланса мощностей при прямом
направлении потока энергии, принимая
М=0,
можно записать так:
О![]() ткуда
ткуда
Соответственно для обратного направления потока механической энергии
![]()
Необходимо иметь в виду, что КПД передач зависит от нагрузки, а для червячного зацепления - и от направления передачи энергии, поэтому при расчетах для правильного определения Мс следует использовать соответствующие зависимости мех от полезной нагрузки передач.
