41)Приведение к скорости двигателя сил сопротивления в элементе поступательного движения

Сила сопротивления в механизме F_СМ , направлена по оси поступательного движения.

Рассмотрим приведение F_СМ при двигательном ре­жиме работы электропривода. В этом случае поток энергии направлен от двигателя к рабочей машине. Уравнение баланса мощности запишется следующим образом :

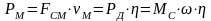, (1)

где 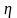- общий КПД передач и рабочей машины.

Из (1) определяется статический момент сопротивления, приве­денный к валу двигателя :

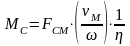, (2)

Из (2) определяется статическое усилие, приведенное к валу двигателя :

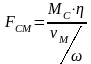. (3)

Здесь отношение (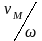 ) является обобщенным передаточным отношением между рабочей машиной и двигателем.

42) Получение трех массовой расчетной модели в результате приведения к скорости двигателя параметров кинематической схемы. Система уравнений

М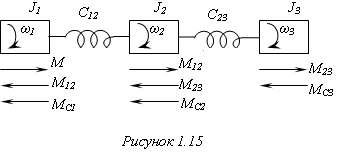 оменты инерции ; ; ,

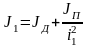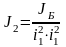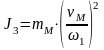1) для упругого вытягивания каната с коэффициентом жесткости

,

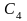
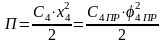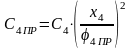
Так как скорость упругой деформации в реальном и эквивалентном упругих элементах одна и та же, то 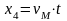, , 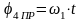откуда ;

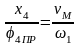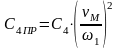
2) для упругого закручивания вала барабана с коэффициентом жесткости

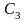
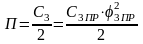,откуда

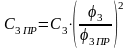
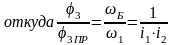
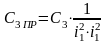
3) для упругого закручивания промежуточного вала с коэффициентом жесткости

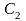
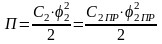, откуда так как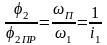 , то .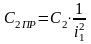

Заменяя одним упругим элементом получим

, , , .

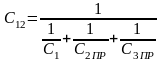
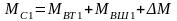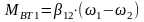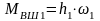Здесь 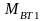- момент внутреннего вязкого трения в упругом элементе, 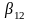- коэффициент внутреннего вязкого трения в Нм∙с. На вторую массу с моментом инерции 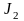действует момент сопротивления ,

, . ,

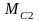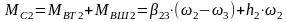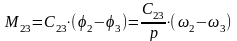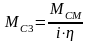Таким образом, движение трехмассовой механической системы электропривода можно описать следующей системой из 3-х уравнений движения, записанных для каждой из вращающихся масс:

;

;

.

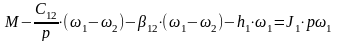
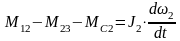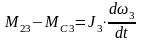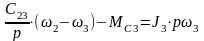
43) Одержання двомасової розрахункової динамічної моделі в результаті приведення до швидкості двигуна параметрів кінематичної схеми. Система рівнянь.

Н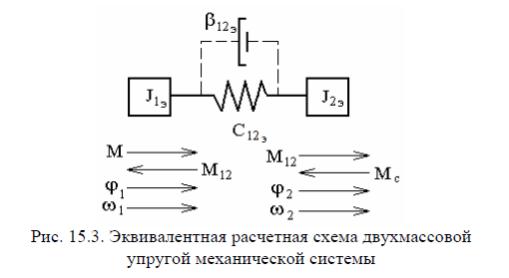 а практике чаще используют эквивалентную расчетную схему двухмассовой упругой системы к которой приводят многомассовую механическую систему. В схеме обобщенными координатами являются угловые перемещения масс ϕ₁, ϕ₂ и соответствующие им обобщенные угловые скорости ω₁, ω₂. Статические моменты, обусловленные силами трения в элементах кинематической цепи первой (J_1Э) и второй (J_2Э) масс, ввиду

и х малости приняты равными нулю. В расчетной схеме действуют: М – момент двигателя, M₁₂ – момент упругой деформации, М_с – статический момент исполнительного органа рабочей машины. Кроме того, на схеме приведены: C₁₂ – жесткость упругой связи между массами, β_12э – коэффициент внутреннего вязкого трения. Используем уравнение Лагранжа для получения математической модели двухмассовой механической части ЭП. Запас кинетической энергии и обобщенные координаты Элементарные работы, совершаемые действующими силами, приложенными к первой (δА₁) и второй (δА₂) массам:

Тогда уравнения Лагранжа для двухмассовой механической части электропривода будут иметь следующий вид.

Для первой массы:

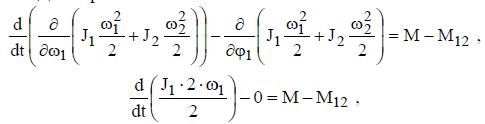
Д ля второй массы в результате аналогичных вычислений получаем:

О чевидно, что эти уравнения являются аналогами основного уравнения движения ЭП. Для полного описания динамики необходимо уравнение для М₁₂.

В окончательном виде получим

М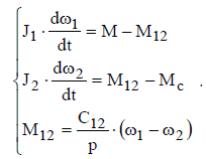 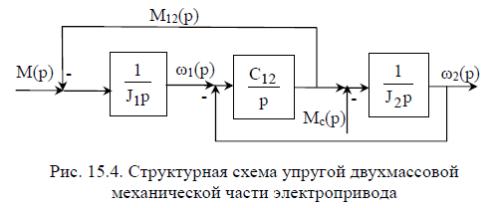атематическая модель двухмассовой упругой механической части электропривода получается из последних уравнений:

В данной математической модели отсутствует учет диссипативных сил – внутреннего трения, определяемых коэффициентом внутреннего вязкого трения β₁₂, и внешнего трения, поскольку статические моменты, обусловленные силами трения в элементах кинематической цепи первой и второй масс были приняты равными нулю.

44) Одержання одно масової розрахункової динамічної моделі в результаті її перетворення з двомасової моделі за умови С₁₂ = бесконечности

Электромеханическая система с 2-х массовой упругой механической частью представляет собой простейшую модель электропривода, наиболее удобную для изучения влияния упругих связей.

В тех случаях, когда влияние упругих связей незначительно или при решении задачи ими можно пренебречь, механическая часть электропривода представляется простейшей расчетной схемой – жестким приведенным механическим звеном, т.е. многомассовая механическая часть эл.привода с моментами инерциями J1 ,J2 и т.д. заменяется действием одного момента инерции J_np, приведенного к расчетной скорости. Суммарный приведенный момент инерции эл.привода в этом случае определяется как 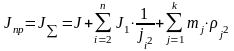, где

J – момент инерции двигателя; n, k – число элементов установки, совершающих соответственно вращательное и поступательное движение.

Суммарные приведенный к валу двигателя момент статического сопротивления в общем виде можно представить как: 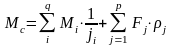, где

p,q – число внешних моментов М_i и сил F_j, приложенных к системе кроме электромагнитного момента двигателя.