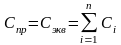36)Приведение к скорости двигателя момента инерции элемента кинематической схемы

П од приведением момента инерции J_пр, к расчетной скорости (валу двигателя) понимают момент инерции простейшей системы, состоящей только из элементов, вращающихся со скоростью оси, к которой производится приведение, и который обладает при этом запасом кинетической энергии, равной запасу энергии в исходной системе.

В этом случае:

Отсюда: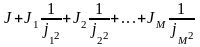

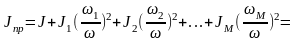
Где j₁,j₂,…,j_n – передаточные отношения между осью (валом) двигателя и осями отдельных вращающихся элементов (звеньев).

Ч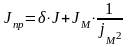 асто приведенный момент инерции системы считают равным сумме моментов инерции двигателя и приведенного момента инерции рабочей машины, а моменты инерции звеньев передаточного механизма (редуктора) учитывают увеличением момента инерции двигателя в “” раз, т.е.

, где =1,11,3. При привидении момента любого i-го элемента к расчетной скорости должно выполняться условие: 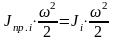, откуда 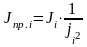.Аналогично выполняется приведение масс, движущихся поступательно со скоростью V, к расчетной скорости .

Баланс кинетической энергии Отсюда

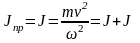
В этом случае приведенная к вращательному движению масса эквивалентна моменту инерции J `

В общем случае приведение поступательно движущейся со скоростью V_j массы m_j к расчетной скорости  производится из условий равенства запасов энергии: ;

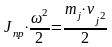Отсюда 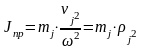, где j – радиус приведения к расчетной скорости (валу двигателя) j-го поступательно движущегося элемента.

37Приведение к скорости двигателя массы элемента поступательного движения.

Приведение моментов инерции и поступательно движущихся масс. Для решения этих задач приведения необходимо составить уравнений баланса кинетической энергии в системе, выражая общий запас её либо через момент инерции, приведенный к вращательному движению двигателя 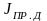, либо через так называемую приведенную массу, т.е. массу, приведенную к поступательному движению механизма т_ПР.М. Таким образом, для кинематической схемы (рис. 1.8), уравнения баланса кинетической энергии записываются в следующем виде:

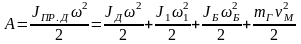; (1.24)

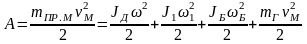. (1.25)

Из (1.24) определяется приведенный к валу двигателя момент инерции си­стемы

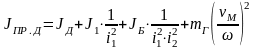. (1.26)

Из (1.25) определяется масса системы, приведенная к оси движения ме­ханизма

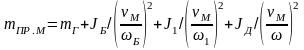. (1.27)

3 8.Приведення до швидкостi двигуна жорсткостi пружного елемента обертального руху

Приведение жесткостей упругих элементов осуществляется при условии сохранения неизменной величины потенциальной энергии деформации реальной и эквивалентной систем.

Отметим, что приведенной жесткостью элемента называется крутящий момент (усилие), необходимый для получения крутильной деформации упругого элемента 1 радиан (или линейной деформации 1 м).

Приведенная жесткость может быть определена, если известен фактический

коэффициент жесткости упругого элемента и кинематические параметры системы. Пусть, например, участок кинематической цепи с жесткостью С_i (см. рис.) при закручивании получает деформацию _i радиан. Потенциальная энергия деформации при этом 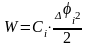Эквивалентный упругий элемент должен иметь такую же потенциальную энергию. 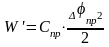, где __пр – угол поворота оси приведения при закручивании упругого элемента на величину _i, а С_пр – приведенная жесткость эквивалентного элемента. Если жесткость упругого элемента проводится к скорости вала двигателя и передаточное число между их осями 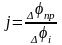, тогда из условия W=W’, получим 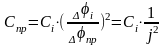Т.о., для определения С_пр любого упругого элемента, испытывающего крутильную деформацию, необходимо его жесткость С_i разделить на квадрат j между этим элементом и осью приведения. Аналогично осуществляется приведение жесткостей упругих элементов с линейными деформациями растяжения или сжатия. Так, для упругого каната, имеющего жесткость C_k=C_j и линейную деформацию _S (см. рис.), потенциальная энергии деформации 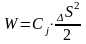Потенциальная энергия эквивалентного упругого элемента, подвергающегося крутильной деформации . Приравнивая, найдем 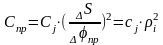. 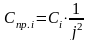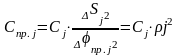В общем случае ; , где 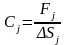-жесткость упругого линейного элемента. При наличии в системе “n” последовательно соединенных упругих элементов, имеющих различную жесткость и движущихся с одинаковыми скоростями, они могут быть заменены одним элементом с эквивалентной (приведенной) жесткостью исходя из соотношения 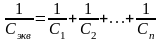или . 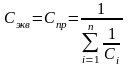Если скорости упругих элементов, соединенных последовательно разные, жесткость каждого из них необходимо привести к расчетной скорости и только после этого определяется С_экв. Если упругие элементы соединены параллельно (например, при подвешивании сосуда на нескольких канатах), приведенная жесткость всей системы