Статистика осуществляет классификацию индексов по следующим признакам:
1. В зависимости от объекта исследования:
индексы объемных (количественных) показателей (индексы физического объема: товарооборота, продукции, потребления)
индексы качественных показателей (индексы цен, себестоимости, заработной плата)
К индексам объемных показателей относятся индексы физического объема: товарооборота, продукции, потребления материальных благ и услуг; а также других показателей, имеющих количественный характер: численности работников, посевных площадей и т.п. К индексам качественных показателей относятся индексы: цен, себестоимости продукции, заработной платы, производительности труда, урожайности и т.п.;
2. По степени охвата элементов совокупности:
индивидуальные индексы (дают сравнительную характеристику отдельных элементов явления)
общие индексы (характеризуют изменение совокупности элементов или всего явления в целом)
3. В зависимости от методологии исчисления общие индексы подразделяются на:
агрегатные (агрегатные индексы являются основной формой индексов и строятся как агрегаты путем взвешивания индексируемого показателя с помощью неизменной величины другого, взаимосвязанного с ним показателя).
средние (являются производными от агрегатных)
4. В зависимости от базы сравнения различают:
базисные (если при исчислении индексов за несколько периодов времени база сравнения остается постоянной)
цепные (если база сравнения постоянно меняется)
16) В зависимости от методологии расчета индивидуальных и сводных индексов различаютсредние арифметические и средние гармонические индексы. Другими словами, общий индекс, построенный на базе индивидуального индекса, принимает форму среднего арифметического или гармонического индекса, т. е. он может быть преобразован в средний арифметический и средний гармонический индексы.
Идея построения сводного индекса в виде средней величины из индивидуальных (групповых) индексов вполне объяснима: ведь сводный индекс является общей мерой, характеризующей среднюю величину изменения индексируемого показателя, и, конечно, его величина должна зависеть от величин индивидуальных индексов. А критерием правильности построения сводного индекса в форме средней величины (среднего индекса) является его тождественность агрегатному индексу.
Преобразование агрегатного индекса в средний из индивидуальных (групповых) индексов производится следующим образом: либо в числителе, либо в знаменателе агрегатного индекса индексируемый показатель заменяется его выражением через соответствующий индивидуальный индекс. Если такую замену сделать в числителе, то агрегатный индекс будет преобразован в средний арифметический, если же в знаменателе – то в средний гармонический из индивидуальных индексов.
Например, известен индивидуальный индекс физического объема iq = q1/q0 и стоимость продукции каждого вида в базисном периоде (q0p0). Исходной базой построения среднего из индивидуальных индексов служит сводный индекс физического объема:
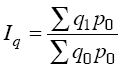
(агрегатная форма индекса Ласпейреса).
Из имеющихся данных непосредственно суммированием можно получить только знаменатель формулы. Числитель же может быть получен перемножением стоимости отдельного вида продукции базисного периода на индивидуальный индекс:
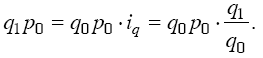
Тогда формула сводного индекса примет вид:
т. е. получим средний арифметический индекс физического объема, где весами служит стоимость отдельных видов продукции в базисном периоде.
Допустим, что в наличии имеется информация о динамике объема выпуска каждого вида продукции (q) и стоимости каждого вида продукции в отчетном периоде (p1q1). Для определения общего изменения выпуска продукции предприятия в этом случае удобно воспользоваться формулой Пааше:
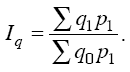
Числитель формулы можно получить суммированием величин q1P1, а знаменатель – делением фактической стоимости каждого вида продукции на соответствующий индивидуальный индекс физического объема продукции, т. е. делением: p1q1/iq, тогда:
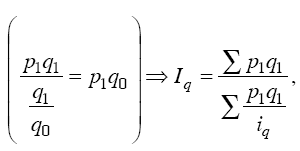
таким образом, получаем формулу среднего взвешенного гармонического индекса физического объема.