11. Условия применения выборочного метода в торговле. Этапы выборочного исследования.

Выборочное наблюдение относится к разновидности несплошного наблюдения. Оно охватывает отобранную часть единиц генеральной совокупности. Цель выборочного наблюдения - по отобранной части единиц дать характеристику всей совокупности единиц. Чтобы отобранная часть была репрезентативна (т.е. представляла всю совокупность единиц), выборочное наблюдение должно быть специально организовано. Следовательно, в отличие от генеральной совокупности, представляющей всю совокупность исследуемых единиц, выборочная совокупность представляет ту часть единиц генеральной совокупности, которая является объектом непосредственного наблюдения.

По понятным причинам выборочный метод может широко использоваться органами государственной статистики. Он позволяет при значительной экономии средств и затрат получать необходимую достоверную информацию. Гарантия репрезентативности обеспечивается применением научно обоснованных способов отбора единиц, которые подлежат обследованию.

Следует сразу же иметь в виду, что при сопоставлении показателей по результатам выборочного исследования с характеристиками для всей генеральной совокупности могут иметь место отклонения. Величина этих отклонений называется ошибкой наблюдения, которая может быть или ошибкой регистрации(несовершенство технических условий), или ошибкой репрезентативности (случайное или систематическое нарушение правил при отборе единиц).

Выборочным является наблюдение, при котором характеристика всей совокупности фактов дается по некоторой их части, отобранной в случайном порядке. Выборочное наблюдение широко применяется в различных отраслях, например, в торговле с его помощью изучают эффективность новых, передовых форм торговли, спрос населения и степень его удовлетворения.

Выборочное наблюдение дает возможность, не прибегая к сплошному учету, получить обобщающие показатели, которые правильно отражают характеристики всей совокупности.

Преимущества выборочного метода по сравнению со сплошным:

1. короче время проведения

2.мин-е затраты труда и средств.

Генеральная совокупность – вся совокупность единиц, из которых производится отбор.

Выборочная совокупность (выборка) – совокупность единиц, отобранная для проведения выборочного наблюдения.

На практике по тем или иным причинам не всегда возможно или же нецелесообразно рассматривать всю генеральную совокупность. Тогда ограничиваются изучением лишь некоторой части ее, конечной целью которого является распространение полученных результатов на всю генеральную совокупность, т. е. применяют выборочный метод.

Теоретической основой выборочного метода является закон больших чисел. В силу этого закона при ограниченном рассеивании признака в генеральной совокупности и достаточно большой выборке с вероятностью, близкой к полной достоверности, выборочная средняя может быть сколь угодно близка к генеральной средней. Закон этот, включающий в себя группу теорем, доказан строго математически. Таким образом, средняя арифметическая, рассчитанная по выборке, может с достаточным основанием рассматриваться как показатель, характеризующий генеральную совокупность в целом.

Разумеется, не всякая выборка может быть основой для характеристики всей совокупности, к которой она принадлежит. Таким свойством обладают лишь репрезентативные (представительные) выборки, т. е. выборки, которые правильно отражают свойства генеральной совокупности.

Этапы выборки:

1. Постановка цели наблюдения.

2. Составление программы проведения.

3. Определение доли выборки и способа отбора единиц в выборку.

4. Проведение наблюдения, т.е. регистрация величины признака у отобранных единиц.

5. Обобщение данных и расчет выборочных характеристик.

6. Распространение выборочных данных на генеральную совокупность.

В статистике различают следующие виды выборок:

1.    Собственно случайная выборка, суть которой состоит в том, что отбирают единицы по жребию. Отбор осуществляется повторный и бесповторный. Повторный отбор, при котором единицы совокупности участвуют столько раз, сколько происходит наблюдение. Бесповторный отбор – единица, выбранная раз, больше не участвует.

2.    Механическая выборка. Генеральную совокупность механически разбивают на столько частей, сколько надо отобрать в выборку, а затем из каждой части механически отбирают единицы. Механическая выборка производится только бесповторным способом.

3.    Типическая выборка. Генеральная совокупность также разбивается на группы, но обязательно по какому-то признаку, а затем из каждой группы случайным или механическим способом отбирают нужное число единиц.

4.    Серийная. Отбирают не отдельные единицы, а целые группы или серии. Затем обследуют все единицы отобранных групп. Способ отбора случайный, либо механический, но бесповторным способом.

5.    Многоступенчатая выборка. Типически отобранная часть сочетается с несколькими стадиями или ступенями отбора, причем на каждой ступени выбирается своя единица.

6.    Многоразовая. Сохраняется одна и та же единица совокупности.

7.    Комбинированная. Выборочное наблюдение сочетается со сплошным.

8.    Моментное наблюдение. Фиксируются не единицы совокупности, а состояние явления.

9.    Малая выборка. Число единиц до 20.

12. Общая тенденция (тренд) ряда динамики. Статистические методы выявления и математической оценки тренда.

Методы анализа основной тенденции ряда динамики

Основной тенденцией ряда динамики (или трендом) называ­ется устойчивое изменение уровня явления во времени, обусловлен­ное влиянием постоянно действующих факторов и свободное от слу­чайных колебаний.

В случаях, когда уровни динамического ряда непрерывно растут или непрерывно снижаются, основная тенденция ряда является оче­видной. Однако достаточно часто уровни динамических рядов пре­терпевают различные изменения (т. е. то растут, то убывают), и общая тенденция неясна. Задача статистики заключается в выявлении тен­денции в таких рядах. С этой целью ряды динамики подвергаются об­работке методами укрупнения интервалов, скользящей средней и аналитического выравнивания.

Общая тенденция развития явления во времени – это поступательное непрерывное изменение ур-ней РД за длит. Промежуток времени в опр. Направлении.

Тренд – это некот. аналит. ф-я, при пом. кот. описывают тенденцию РД.

Одна из важнейших задач статистики- определение в рядах динамики общей тенденции развития.

Основной тенденцией развития называется плавное и устойчивое изменение уровня во времени, свободное от случайных колебаний. Задача состоит в выявлении общей тенденции в изменении уровней ряда, освобожденной от действия различных факторов.

Изучение тренда включает два основных этапа:

• ряд динамики проверяется на наличие тренда;

• производится выравнивание временного ряда и непосредственно выделение тренда с экстраполяцией полученных результатов.

С этой целью ряды динамики подвергаются обработке методами укрупнение интервалов, скользящей средней и аналитического выравнивания:

1. Метод укрупнения интервалов.

Одним из наиболее элементарных способов изучения общей тенденции в ряду динамики является укрупнение интервалов. Этот способ основан на укрупнении периодов, к которым относятся уровни ряда динамики. Например, преобразование месячных периодов в квартальные, квартальных в годовые и т.д.

2. Метод скользящей средней.

Выявление общей тенденции ряда динамики можно произвести путем сглаживания ряда динамики с помощью скользящей средней.

Скользящая средняя- подвижная динамическая средняя, которая рассчитывается по ряду при последовательном передвижении на один интервал, то есть сначала вычисляют средний уровень из определенного числа первых по порядку уровней ряда, затем- средний уровень из такого же числа членов, начиная со второго. Средняя как бы скользит по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий.

При этом посредством осреднения эмпирических данных индивидуальные колебания погашаются, и общая тенденция развития явления выражается в виде некоторой плавной линии (теоретические уровни). И так, суть метода заключается в замене абсолютных данных средними арифметическими за определенные периоды.

Скользящая средняя обладает достаточной гибкостью, но недостатком метода является укорачивание сглаженного ряда по сравнению с фактическим, что ведет к потери информации. Кроме того, скользящая средняя не дает аналитического выражения тренда.

Период скользящей может быть четным и нечетным. Практически удобнее использовать нечетный период, так как в этом случае скользящая средняя будет отнесена к середине периода скольжения. Скользящие средние с продолжительностью периода, равной 3, следующие:

; ; и т.д.

Полученные средние записываются к соответствующему срединному интервалу.

Особенность сглаживания по четному числу уровней состоит в том, что каждая из численных (например, четырехчленных) средних относится к соответствующим промежуткам между смежными периодами. Для получения значений сглаженных уровней соответствующих периодов необходимо произвести центрирование расчетных средних.

Недостатком способа сглаживания рядов динамики является то, что полученные средние не дает теоретических рядов, в основе которых лежала бы математически выраженная закономерность.

3. Метод аналитического выравнивания.

Более совершенным приемом изучения общей тенденции в рядах динамики является аналитическое выравнивание. При изучении общей тенденции методом аналитического выравнивания исходят из того, что изменения уровней ряда динамики могут быть с той или иной степенью точности приближения выражены определенными математическими функциями. Вид уравнения определяется характером динамики развития конкретного явления. Логический анализ при выборе вида уравнения может быть основан на рассчитанных показателях динамики, а именно:

• если относительно стабильны абсолютные приросты (первые разности уровней приблизительно равны), , сглаживание может быть выполнено по прямой;

• если абсолютные приросты равномерно увеличиваются (вторые разности уровней приблизительно равны), можно принять параболу второго порядка;

• при ускоренно возрастающих или замедляющихся абсолютных приростах - параболу третьего порядка;

• при относительно стабильных темпах роста- показательную функцию.

Для аналитического выравнивания наиболее часто используются следующие виды трендовых моделей: прямая (линейная), парабола второго порядка, показательная (логарифмическая) кривая, гиперболическая.

Цель аналитического выравнивания- определение аналитической или графической зависимости. На практике по имеющемуся временному ряду задают вид и находят параметры функции, а затем анализируют поведение отклонений от тенденции. Чаще всего при выравнивании используются следующие зависимости; линейная, параболическая и экспоненциальная.

После выяснения характера кривой развития необходимо определить ее параметры, что можно сделать различными методами:

1. решением системы уравнений по известным уровням ряда динамики;

2. методом средних значений (линейных отклонений), который заключается в следующем: ряд расчленяется на две примерно равные части, и вводятся преобразования, чтобы сумма выровненных значений в каждой части совпала с суммой фактических значений, например, в случае выравнивания прямой линии ;

3. выравниванием ряда динамики с помощью метода конечных разностей;

4. методом наименьших квадратов: это некоторый прием получения оценки детерминированной компоненты , характеризующих тренд или ряд изучаемого явления.

Во многих случаях моделирование рядов динамики с помощью полиномов или экспоненциальной функции не дает удовлетворительных результатов, так как в рядах динамики содержатся заметные периодические колебания вокруг общей тенденции. В таких случаях следует использовать гармонический анализ.

Экстраполяция тенденции как метод прогнозирования.

Основа большинства методов прогнозирования- экстраполяция тенденции, связанная с распространением закономерностей, связей и соотношений, действующих в изучаемом периоде, за его пределы или, другими словами, это получение представлений о будущем на основе информации, относящейся к прошлому и настоящему.

Экстраполяция, проводимая в будущее,- это перспектива, а в прошлое,- ретроспектива.

Предпосылки применения экстраполяции:

• развитие исследуемого явления в целом следует описывать плавной кривой;

• общая тенденция развития явления в прошлом и настоящем не должна претерпевать серьезных изменений в будущем.

Экстраполяцию в общем виде можно представить так:

,

где - прогнозируемый уровень; - текущей уровень прогнозного ряда;

Т- срок экстраполяции; - параметр уравнения тренда.

При этом могут использоваться разные методы в зависимости от исходной информации.

Упрощенные приемы целесообразны при недостаточной информации о предыстории развития явления (нет достаточно длинного ряда или информация заданна только двумя точками: на начало и конец периода). Упрощенные приемы основываются на средних показателях динамики, и можно выделить:

1. Метод среднего абсолютного прироста.

Для нахождения интересующего нас аналитического выражения тенденции на любую дату необходимо определить средний абсолютный прирост и последовательно прибавить его к последнему уровню ряда столько раз, на сколько периодов экстраполируется ряд.

,

где t- срок прогноза; i- номер последнего уровня.

Применение в экстраполяции среднего абсолютного прироста предполагает, что развитие явления происходит по арифметической прогрессии и относится в прогнозировании к классу «наивных» моделей, ибо чаше всего развитие явления следует по иному пути, чем арифметическая прогрессия Т.С. Вместе с тем в ряде случаев этот метод может найти применение как предварительный прогноз, если у исследователя нет динамического ряда: информация дана лишь на начало и конец периода (например, данные одного баланса).

2. Метод среднего темпа роста.

Осуществляется, когда общая тенденция характеризуется показательной кривой

,

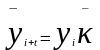где - последний уровень ряда динамики; k- средний коэффициент роста.

3. Выравнивание рядов по какой-либо аналитической формуле.

Экстраполяция дает возможность получить точечное значение прогнозов. Точное совпадение фактических данных и прогнозных точечных оценок, полученных путем экстраполяции кривых, имеет малую вероятность.

Любой статистический прогноз носит приближенный характер, поэтому целесообразно определение доверительных интервалов прогноза:

, ,

где - коэффициент доверия по распределению Стьюдента при уровне значимости ; - средняя квадратическая ошибка тренда; k- число параметров в уравнении; - расчетное значение уровня.

Аналитические методы основаны на применении метода наименьших квадратов к динамическому ряду и представлении закономерности развития явления во времени в виде уравнения тренда, то есть математической функции уровней динамического ряда (y) от факторного времени (t): y=f(t).

Аналитическое сглаживание позволяет не только определить общую тенденцию изменения явления на рассматриваемом отрезке времени, но и выполнять расчеты для таких периодов, в отношении которых нет исходных данных.

Адаптивные методы используются в условиях сильной колеблемости уровней динамического ряда и позволяют при изучении тенденции учитывать степень влияния предыдущих уровней на последующие значения динамического ряда. К адаптивным методам относятся методы скользящих и экспоненциальных средних, метод гармонических весов, методы авторегрессионных преобразований.

Цель адаптивных методов заключается в построении самонастраивающихся моделей, способных учитывать информационную ценность различных членов временного ряда и давать достаточно точные оценки будущим членам данного ряда. ТС

Прогноз получается как экстраполяция последней тенденции. В разных методиках прогнозирования процесс настройки (адаптации) модели осуществляется по-разному, и можно выделить:

1. метод скользящей средней (адаптивной фильтрации, метод Бонса-Дженкинса);

2. метод экспоненциального сглаживания (методы Хольда, Брауна, экспоненциальной средней).

Скользящие средние представляют собой средние уровни за определенные периоды времени путем последовательного передвижения начала периода на единицу времени. При простой скользящей средней все уровни временного ряда считаются равноценными, а при исчислении взвешенной скользящей средней каждому уровню в пределах интервала сглаживания приписывается вес, зависящий от расстояния данного уровня до середины интервала сглаживания.

Особенность метода экспоненциального сглаживания в том, что в процедуре выравнивания каждого наблюдения используется только значения предыдущих уравнений, взятых с определенным весом. Смысл экспоненциальных средних состоит в нахождении таких средних, в которых влияние прошлых наблюдений затухает по мере удаления от момента, для которого определяется средние.

Методика построения трендовой модели:

1. Факт. ур-ни РД изобр. На линейном графике.

2. По хар-ру расположения точек на графике подбираем мат. функ-ю.

3. Параметры ур-ний выч-ся по способу наименьших квадратов

4. Промежуточные расчеты. Есть упрощенный способ расчета параметров – способ отсета времени от условного нуля. За него берется середина РД. При четном числе – 2 средних значения берутся за – и +1, прибавляется по +-2, а если нечетное, то середина=0, прибавляется по +-1. Параметр а2= ср. коэф. Роста.

5. Вычисление параметров.

6. Вычисление теор. значений.- послед-но подставляем t в полученную тренд. модель.

7. Проверка правильности расчетов - сумма y ср. ti=сумма yi

8. Проверка адекватности тренд. модели.

   1. Визуальная оценка – теор. ур-ни переносим на график.

   2. Мат. оценка, произв. по стандартиз-й ошибке аппроксимации

G(дельта большая, как у дисперсии) y ср. ti = корень(сумма(yi-yti)квадрат / n)

13. Особенности сбора и обработки статистической информации в современных условиях.

 Статистическая информация есть совокупность различных сведений, подлежащих фиксации, передаче, преобразованию, хранению и использованию для принятия решений в различных областях. Для статистической информации характерны большие объемы, ограниченные сроки обработки, многократное получение и анализ, абсолютные выражения исходных данных и относительные результаты расчетов, единство рассчитываемых показателей для различных сфер деятельности, длительное хранение данных .

Статистические показатели описывают характеристики объекта статистического наблюдения.   Статистическая информация может быть организована иерархически, т. е. на каждом уровне данные могут быть укрупнены (агрегированы) на основе некоторых признаков группировки (территориального, функционального и др.).

Статистический отчет — это документ, содержащий совокупность показателей, сгруппированных по определенным признакам. Каждый отчет имеет определенную форму (графы и строки) и содержание (показатели). Однородные отчеты могут быть объединены на основании определенного признака, образуя массив (совокупность отчетов), а разнородные массивы объединяются в совокупность статистических документов, характеризующую определенный объект статистического наблюдения.

Любая система статистики призвана организовывать движение потоков статистической информации от мест возникновения к потребителям. В государственной статистической системе источниками первичной информации являются предприятия и организации различных отраслей, а потребителем — Госкомстат РФ, который формирует сводную статистическую отчетность в соответствующих разрезах и предоставляет ее в органы управления различного уровня. В простых (частных, локальных) статистических системах источники и потребители информации могут находиться в пределах одного предприятия или даже являться одним и тем же объектом.

Статистическая обработка данных является одной из сфер, требующих выполнения большого объема сложных и трудоемких математических расчетов, работы с большими массивами исходных данных. К основным предпосылкам применения современных информационных технологий в этой области можно отнести следующие:    • большое количество объектов статистического наблюдения, многомерность данных;    • необходимость отслеживания динамики массива показателей во времени, формирования сводок по различным разрезам;    • трудность получения достоверных данных в доступном для анализа виде;    • высокие материальные и трудовые затраты на проведение статистических работ;    • низкая оперативность обработки данных;    • территориальная разобщенность исходных данных, необходимость их интеграции и одновременной обработки;    • объемность хранимых данных и трудность доступа к ним;    • сложность математических методов анализа данных;    • относительная стабильность форм статистической отчетности.

Статистические информационные системы предназначены для автоматизации работ в области статистики и позволяют собирать, хранить и обрабатывать разнородные массивы данных с использованием единой информационной базы. Структура статистической информационной системы соответствует определенному уровню в организационной структуре органов государственного управления (федеральному, региональному или местному), и на этом уровне

С точки зрения состава выполняемых функций, статистическая информационная система обеспечивает комплекс работ по сбору, фиксации динамики изменения и анализу взаимосвязанных показателей, характеризующих конкретный объект статистического наблюдения. Совокупность статистических работ с конкретной группой показателей может составлять основу для выделения функциональной подсистемы статистической информационной системы.    Для организации однократного ввода исходных данных и их многократного использования при решении различных задач, для поддержания полноты и достоверности данных, исключения дублирования информации в основе статистической системы лежит единая информационная база. Единство технической базы обеспечивает также совместимость нескольких статистических информационных систем и свободу интеграции статистических данных и результатов их обработки.    Технология многоуровневой территориально-распределен- ной обработки информации с использованием статистических информационных систем включает следующие основные этапы:    • запуск статистической информационной системы, загрузка информационной базы и библиотек    • при необходимости — корректировка существующих данных;    • выбор форм первичных статистических документов и их визуальный контроль;    • контроль и корректировка введенных данных;    • резервное копирование информационной базы;    • контроль таблиц и пересчет показателей в случае корректировки первичных данных;    • печать контрольных и справочных сведений о передаваемой информации;    • оценка справочной информации и контроль таблиц, полученных с каждого из объектов нижнего уровня;    • формирование каталога по территориальным и другим разрезам;    • передача электронных материалов на федеральный уровень;    • сбор и агрегация данных с нижних уровней,    • передача агрегированных данных на нижние уровни.    В динамично развивающейся рыночной ситуации для принятия решений руководству предприятия важно иметь актуальную информацию о внешней среде. В то же время руководству необходима достоверная информация о состоянии и возможностях самого предприятия, динамике изменения показателей его деятельности, о направлениях развития и т. д.    В сложившихся условиях статистический учет на предприятии изменяется и ориентируется на потребности руководства при выполнении функций управления на основе внутренних и внешних статистических данных. Изменяется также технология машинной реализации статистического учета, появляется задача создания статистической информационной системы предприятия, способной интегрироваться не только с ИС управления предприятием, но и с внешней информационной средой.    При создании статистической информационной системы предприятия необходимо оценить выполняемые руководством функции и решаемые задачи, определить его потребность в статистической информации, уточнить цели и задачи статистической ИС, выбрать статистические показатели и методы их расчета, определить состав математико-статистических методов, обеспечивающих поддержку принятия решений на основе статистической информации. Перед переходом к непосредственному проектированию необходимо выбрать принципы создания и функционирования статистической ИС, и лишь затем поэтапно проектировать ее на макро- и микроуровнях. Проектирование завершается этапом внедрения статистической ИС на конкретном предприятии.    К основным особенностям статистических ИС предприятия можно отнести следующие:    • высокая оперативность;    • альтернативность расчетов (вариантность);    • использование математико-статистических методов для получения конкретных выводов на основе анализа полученной исходной информации;    • ориентация на прогнозы;    • интегрируемость;    • активность.    С точки зрения интегрируемости можно выделить локальные и интегрированные статистические пакеты.    Локальные (автономные) статистические ИС могут быть использованы самостоятельно, т. е. без согласования с существующей информационно-технологической системой управления предприятием. Однако это влечет за собой ряд проблем, связанных с необходимостью многократного ввода одних и тех же первичных данных, поддержания информации в актуальном состоянии и т. д.    Интегрированные статистические ИС опираются на единую информационную базу первичных данных, которая является источником информации для выполнения всех функций управления на предприятии. Это позволяет многократно использовать выходные данные конкретного этапа обработки в качестве входных данных для выполнения других этапов и тем самым избежать необходимости повторного ввода первичных данных для составления различных статистических отчетов. Такой подход позволяет автоматически получать в электронном виде все необходимые статистические показатели и отчеты, быстро обрабатывать данные с помощью аналитических программ, легко корректировать форму статистических отчетов, а при наличии телекоммуникационных средств — пересылать отчеты в соответствующие вышестоящие организации.    Свойство активности позволяет разделить статистические ИС на активные, пассивные либо частично активные системы.    Активные статистические ИС способны анализировать состояние предприятия по оперативно поступающим данным, выявлять несоответствия и противоречия, вырабатывать совокупность альтернативных вариантов разрешения каждой ситуации, представлять ее руководству предприятия без его предварительного запроса.    Пассивные статистические ИС предприятия не осуществляют никаких действий без запроса пользователя и ориентированы только на сбор и обработку информации. Такие системы выдают данные в чистом виде, без их характеристики и оценки, а пользователь может самостоятельно выбирать необходимую информацию, проводить ее анализ, оценивать развитие системы в будущие периоды времени и т. д.    В качестве частично активных систем выступают аналитические пакеты прикладных программ, которые зачастую являются отдельными элементами инструментальных средств статистической информационной системы [    По сравнению с автономными программами пакеты прикладных программ для статистических расчетов имеют единую технологию получения сводных таблиц, интегрируют отдельные программные средства и типизируют проектирование комплексов электронной обработки информации, а также позволяют в короткие сроки реализовать сложные статистические методы, быстро производить обработку больших массивов данных.    В настоящее время при решении статистических задач средствами комплексов электронной обработки информации активно применяются АРМ экономиста-статистика, обеспечивающие более эффективную организацию труда экономистов за счет автоматизации разнообразных функций и прямого доступа к ресурсам информационной базы, установленной непосредственно на рабочем месте экономиста.    АРМ экономиста-статистика позволяет автоматизировать различные направления деятельности сотрудников, занимающихся статистической деятельностью, и обеспечивает:    • снижение трудоемкости процесса обработки информации;    • повышение оперативности использования получаемой статистической информации;    • повышение персональной ответственности исполнителей за качество и достоверность информации, получаемой на рабочем месте [9].   

14. Структурные средние величины в статистике. Практика их применения в экономических исследованиях.

Средняя величина – это обобщающая величина изучаемого признака в исследуемой совокупности, которая отражает его типичный уровень в расчете на единицу совокупности в конкретных условиях места и времени.

Средние величины относятся к обобщающим статистическим показателям, которые дают сводную характеристику массовых общественных явлений, так как строятся на основе большого количества индивидуальных значений варьирующего признака.

Средняя величина отражает то общее, что характерно для всех единиц изучаемой совокупности. В то же время она уравновешивает влияние всех факторов, действующих на величину признака отдельных единиц совокупности, как бы взаимно погашая их. Уровень любого общественного явления обусловлен действием двух групп факторов. Одни из них являются общими и главными, постоянно действующими, тесно связанными с природой изучаемого явления или процесса, и формируют то типичное для всех единиц изучаемой совокупности, которое и отражается в средней величине. Другие являются индивидуальными, их действие выражено слабее и носит эпизодический, случайный характер. Отсюда средняя величина выступает как "обезличенная", которая может отклоняться от индивидуальных значений признаков, не совпадая количественно ни с одним из них. Средняя величина отражает общее, характерное и типичное для всей совокупности благодаря взаимопогашению в ней случайных, нетипичных различий между признаками отдельных ее единиц, так как ее величина определяется как бы общей равнодействующей из всех причин.

Для того, чтобы средняя величина отражала наиболее типичное значение признака, она должна определяться только для совокупностей, состоящих из качественно однородных единиц. Это требование является основным условием научно обоснованного применения средних величин и предполагает тесную связь метода средних величин и метода группировок в анализе социально-экономических явлений.

Необходимо подчеркнуть, что правильное исчисление любой средней величины предполагает выполнение следующих требований:

• качественная однородность совокупности, по которой вычислена средняя величина.

• исключение влияния на вычисление средней величины случайных, сугубо индивидуальных причин и факторов

• при вычислении средней величины важно установить цель ее расчета и так называемый определяющий показатель, на который она должна быть ориентирована.

Средняя величина, рассчитанная в целом по совокупности, называется общей средней - отражает общие черты изучаемого явления; средние величины, рассчитанные для каждой группы групповыми средними - дают характеристику явления, складывающуюся в конкретных условиях данной группы.

1.1 Способы расчета могут быть разные, поэтому в статистике различают несколько видов средней величины

Средние величины делятся на 2 больших вида:

степенные средние (средняя гармоническая, средняя геометрическая, средняя арифметическая и др.). Для вычисления степенных средних необходимо использовать все имеющиеся значения признака. Если рассчитывать все виды степенных средних для одних и тех же данных, то их значения окажутся одинаковыми. Тогда действует правило мажорантности средних: с увеличением показателя степени средних увеличивается и сама средняя величина ( ).

структурные средние (мода, медиана). Мода и медиана определяются лишь структурой распределения. Поэтому их именуют "структурными позиционными средними". Медиану и моду часто используют как среднюю характеристику в тех совокупностях, где расчет средней степенной невозможен или нецелесообразен.

Бывает, что величина средней не совпадает ни с одним из реально существующих вариантов, поэтому в статистическом анализе целесообразно использовать величины конкретных вариантов, занимающие в упорядоченном ряду значений признака вполне определенное положение. Примерами таких величин являются средние мода ( ) и медиана ( ).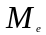

Мода – значение признака, которое имеет наибольшую частоту в статистическом ряду распределения.

Отыскание моды зависит от того, представлен ли варьирующий признак в виде дискретного или интервального ряда. Поиск моды в дискретном ряду происходит путем простого просматривания столбца частот. В этом столбце находится наибольшее число, характеризующее наибольшую частоту. Ей соответствует определенное значение признака, которое и является модой. Может оказаться, что два признака имеют одинаковую частоту. В этом случае ряд будет называться бимодальным.

В интервальном вариационном ряду модой приближенно считают центральный вариант интервала с наибольшей частотой. В таком ряде распределения мода вычисляется по формуле:

Где - нижняя граница модального интервала;

- модальный интервал;

- частота в модальном интервале;

- частота интервала перед модальным интервалом;

- частота интервала после модального интервала.

Мода широко используется в статистической практике при изучении, например, покупательского спроса, регистрации цен и т.д.

Медиана – это вариант, расположенный в центре ранжированного ряда. Медиана делит ряд на две равные части – со значениями признака меньше медианы и со значениями признака больше медианы. Чтобы найти медиану, необходимо отыскать значение признака, которое находится в середине упорядоченного ряда.

В ранжированных рядах несгруппированных данных нахождение медианы сводится к отысканию порядкового номера медианы по формуле:

,

где n – число членов ряда.

В случае четного объема ряда медиана равна средней из двух вариантов, находящихся в середине ряда.

В интервальных рядах распределения медианное значение оказывается в каком-то из интервалов признака x. Этот интервал характерен тем, что его накопленная сумма частот равна или превышает полусумму всех частот ряда. Значение медианы вычисляется по формуле:

,

где 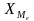- нижняя граница медианного интервала;

- медианный интервал;

- половина от общего числа наблюдений;

- сумма наблюдений, накопленная до начала медианного интервала;

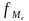- число наблюдений в медианном интервале.

Средний уровень ряда характеризует обобщенную величину абсолютных уровней. Он рассчитывается по средней хронологической, т.е. по средней исчисленной из значений, изменяющихся во времени.