Общее представление о корреляционно-регрессивном анализе

Существующие между явлениями формы и виды связей весьма разнообразны по своей классификации. Предметом статистики являются только такие из них, которые имеют количественный характер и изучаются с помощью количественных методов.

Данный метод содержит две свои составляющие части — корреляционный анализ и регрессионный анализ. Корреляционный анализ — это количественный метод определения тесноты и направления взаимосвязи между выборочными переменными величинами. Регрессионный анализ — это количественный метод определения вида математической функции в причинно-следственной зависимости между переменными величинами.

Для оценки силы связи в теории корреляции применяется шкала английского статистика Чеддока: слабая — от 0,1 до 0,3; умеренная — от 0,3 до 0,5; заметная — от 0,5 до 0,7; высокая — от 0,7 до 0,9; весьма высокая (сильная) — от 0,9 до 1,0.

Ограничения корреляционного анализа

1. Применение возможно при наличии достаточного количества наблюдений для изучения. Число наблюдений должно быть не менее, чем в 5-6 раз превышать число факторов . Если число наблюдений превышает количество факторов в десятки раз, в действие вступает закон больших чисел, который обеспечивает взаимопогашение случайных колебаний.^[13]

2. Необходимо, чтобы совокупность значений всех факторных и результативного признаков подчинялась многомерному нормальному распределениюИсходная совокупность значений должна быть качественно однородной.^[13]

3. Сам по себе факт корреляционной зависимости не даёт основания утверждать, что одна из переменных предшествует или является причиной изменений, или то, что переменные вообще причинно связаны между собой, а не наблюдается действие третьего фактора.^[5]

Область применения

Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи.Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.

Коэффициент корреляции — это величина, которая может варьировать в пределах от +1 до -1. В случае полной положительной корреляции этот коэффициент равен плюс 1, а при полной отрицательной — минус 1. На графике этому соответствует прямая линия, проходящая через точки пересечения значений каждой пары данных:

В случае же если эти точки не выстраиваются по прямой линии, а образуют «облако», коэффициент корреляции по абсолютной величине становится меньше единицы и по мере округления этого облака приближается к нулю:

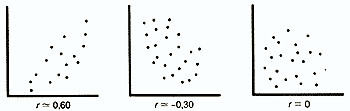
В случае если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга.

Для этого вводится коэффициент корреляции. Он рассчитывается следующим образом:

Есть массив из n точек {x_1,i, _x2,i}

Рассчитываются средние значения для каждого параметра: 

И коэффициент корреляции: 

r изменяется в пределах от -1 до 1. В данном случае это линейный коэффициент корреляции, он показывает линейную взаимосвязь между x₁ иx₂: r равен 1 (или -1), если связь линейна.

Коэффициент r является случайной величиной, поскольку вычисляется из случайных величин.

Методами корреляционного анализа решаются следующие задачи:

1) Взаимосвязь. Есть ли взаимосвязь между параметрами?

2) Прогнозирование. Если известно поведение одного параметра, то можно предсказать поведение другого параметра, коррелирующего с первым.

3) Классификация и идентификация объектов. Корреляционный анализ помогает подобрать набор независимых признаков для классификации.

Регрессио́нный (линейный) анализ — статистический метод исследования влияния одной или нескольких независимых переменных   на зависимую переменную  . Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными.

Цели регрессионного анализа

1. Определение наличия и характера (математического уравнения, описывающего зависимость) связи между переменными

2. Предсказать значение зависимой переменной с помощью независимой

3. Определить вклад независимых переменных в вариацию зависимой

Условия применения

1. Использование метрических переменных

2. Равенство условных дисперсий: D(Y / X) = const;

3. Независимость ошибок от предикторов и нормального их распределения с нулевым средним и постоянной дисперсией;

4. Попарное нормальное распределение всех признаков модели;

5. Независимость предикторов между собой

6. Достаточное количество наблюдений (обычно >15, в зависимости от конкретного характера распределений наблюдений и сложности искомой зависимости)

Уравнение регрессии

Y=a+b*X; где:

Y – зависимая переменная,

a - константа

b - угловой коэффициент

X – независимая переменная

Для многомерной регрессии:

Y = a + b1*X1 + b2*X2 + ... + bp*Xp

8. Основные виды несплошного наблюдения, их значение в новых условиях коммерческой деятельности.

Статистическое наблюдение – это начальная стадия экономико-статистического исследования. Оно представляет собой научно-организованную работу по собиранию массовых первичных данных о явлениях и процессах общественной жизни.

Несплошным называют такое наблюдение, при котором обследованию подвергаются не все единицы изучаемой совокупности, а только заранее установленная их часть. Несплошное наблюдение имеет ряд преимуществ перед сплошным: за счет уменьшения числа обследуемых единиц совокупности они требуют меньших затрат, сил и средств, позволяют применить более детальную программу и более совершенный способ учета фактов, быстрее подводить итоги обследования и повышают оперативность статистического материала.

Несплошное наблюдение организуется по-разному, в зависимости от задачи исследования и характера объекта может быть выборочным, методом основного массива, анкетным, монографическим. Основным видом несплошного наблюдения является выборочное.

Выборочным является наблюдение, при котором характеристика всей совокупности фактов дается по некоторой их части, отобранной в случайном порядке. Выборочное наблюдение широко применяется в различных отраслях, например, в торговле с его помощью изучают эффективность новых, передовых форм торговли, спрос населения и степень его удовлетворения.

Метод основного массива состоит в том, что обследованию подвергается та часть единиц совокупности, у которой величина изучаемого признака является преобладающей во всем объеме.

В анкетном обследовании сбор информации основан на принципе добровольного заполнения адресатами анкет. К нему прибегают при проведении соц. обследования, в торговле для изучения спроса населения на тот или иной товар.

Монографическое обследование представляет собой детальное, глубокое изучение и описание отдельных, характерных в каком-либо отношении единиц совокупности. Монографическое обследование проводится в целях выявления имеющихся или намечающихся тенденций в развитии явления. В торговле с помощью монографического обследования изучается работа магазинов.

Преимущество проведения несплошного наблюдения заключается в том, что оно проводится в короткие сроки, связано с меньшими трудовыми и материальными затратами, полученная информация носит оперативный характер. Существует несколько видов несплошного наблюдения: выборочное, наблюдение основного массива, монографическое.

Применение несплошных статистических методов наблюдения повышает оперативность реагирования на происходящие изменения, обеспечивает управление информацией, позволяющей принимать своев­ременные решения. Периодические выборочные обследования должны стать главным инструментом статистического наблюдения за изменениями массовых социально-экономических явлений, за положением дел в регионах.

Вследствие этого несплошное наблюдение имеет следующие преимущества перед сплошным.

1. Затраты на получение данных лишь от части элементов общей совокупности меньше, следовательно, выборочное обследование является более экономически выгодным, чем сплошное.

2. Объем работы по сбору и обобщению результатов обследования значительно меньше, поэтому результаты выборочного обследования можно получить значительно быстрее, чем при сплошном наблюдении.

3. Так как наблюдению подвергается лишь часть элементов общей совокупности, появляется возможность расширения программы обследования, т.е. более широкого и детального наблюдения каждой единицы в отдельности.

4. При проведении обследования выборочным методом общий объем работы меньше, поэтому можно лучше подготовить и более тщательно контролировать его проведение и обработку данных. Следовательно, выборочное обследование может дать более достоверные результаты, чем соответствующее сплошное.

При решении ряда прикладных статистических задач выборочное наблюдение является единственно возможным. Так, в технологической статистике контроль качества отдельных видов продукции невозможен без нарушения ее потребительских свойств, поэтому он может осуществляться только на основе низкопроцентной выборки. В маркетинговых обследованиях в большинстве случаев также невозможно полностью обследовать всю совокупность потенциальных потребителей того или иного товара.

9. Виды и формы связей, изучаемых в статистике. Задачи статистического изучения связи в торговле.

Изучение стат. явлений формируется и развивается за счет действия на них многих факторов. Статистика при помощи различных методов выявляет эти факторы, определяет наличие связей и форму зависимости между ними.

Рассматривая зависимости между признаками, необходимо выделить, прежде всего, две категории зависимости: 1) функциональные и 2) корреляционные.

Функциональные связи характеризуются полным соответствием между изменением факторного признака и изменением результативной величины, и каждому значению признака-фактора соответствуют вполне определенные значения результативного признака. Функциональная зависимость может связывать результативный признак с одним или несколькими факторными признаками. Так, величина начисленной заработной платы при повременной оплате труда зависит от количества отработанных часов.

В корреляционных связях между изменением факторного и результативного признака нет полного соответствия, воздействие отдельных факторов проявляется лишь в среднем при массовом наблюдении фактических данных. Одновременное воздействие на изучаемый признак большого количества самых разнообразных факторов приводит к тому, что одному и тому же значению признака-фактора соответствует целое распределение значений результативного признака, поскольку в каждом конкретном случае прочие факторные признаки могут изменять силу и направленность своего воздействия.

При сравнении функциональных и корреляционных зависимостей следует иметь в виду, что при наличии функциональной зависимости между признаками можно, зная величину факторного признака, точно определить величину результативного признака. При наличии же корреляционной зависимости устанавливается лишь тенденция изменения результативного признака при изменении величины факторного признака. В отличие от жесткости функциональной связи корреляционные связи характеризуются множеством причин и следствий и устанавливаются лишь их тенденции. Статистические показатели могут состоять между собой в следующих основных видах связи: балансовой, компонентной, факторной и др.

Основные виды связей:

1)Балансовая связь характеризует зависимость между источником формирования ресурсов и их использованием.

Он + П = В + Ок

(где предложение ресурса: Он – остатки на начало периода, П – поступления; использование ресурса: В – выбытие, Ок – остаток на конец периода).

2)Компонентная связь характеризует изменение стат пок-ля за счет изменения компонентов, его образующих.

а=b*c

Ipq=Ip*Iq

(где a – результативный признак, b и с – факторные признаки).

3)Факторная связь проявляется в согласованной вариации изучаемых показателей.

X – факторный признак (признак, от которого зависит другой признак), y – результативный признак (зависит от факторного признака).

Факторные связи принято классифицировать по степени зависимости одного явления от другого:

1. функциональная связь – связь, при кот. величина результативного признака y полностью опр-ся величиной факторного признака х.

y=f(x)

функциональная связь чаще всего встречается в технике, математике и др. точных науках.

2. корреляционная связь проявляется в масс. явлениях общественной жизни. В этом случае нет точного соответствия между х и у. Одному значению факторного признака х может соответствовать несколько значений результативного признака у, т.к. на результат признака у воздействует множество других факторных признаков.

У=f(x) + E, где Е - прочие факторные признаки.

Т.о. влияние факторного признака х проявляется лишь в общем, среднем для всей совокупности.

По направлению связи:

- прямые

- обратные

 Прямая связь – направление изменения результативного признака совпадает с направлением изменения признака фактора, т.е. с увеличением факторного признака увеличивается и результативный и наоборот. Обратная связь – направление изменения результативного признака не совпадает с изменением факторного признака, т.е. при увеличении факторного признака результативный уменьшается и наоборот.

По форме связи:

-линейные (прямолинейные)

-нелинейные (криволинейные)

1. Прямолинейные – с возрастанием величины факторного признака происходит непрерывное возрастание результативного признака и наоборот. Математически такая зависимость представляется уравнением прямой. График представлен в виде прямой. Эту зависимость называют линейной.

2. Криволинейные – с возрастанием величины факторного признака изменение результативного признака происходит неравномерно, направление его может даже меняться. 

Связи:

-парные

-множественные (результативн признак 1, а факторных 2 и более)

Для корреляционных связей есть различия в том случае, если: исследуется связь между одним признаком – фактором и результативным признаком; исследуется связь между несколькими признаками – факторами и результативным признаком. В первом случае имеет место парная связь и парная корреляция, во втором случае многофакторная связь и множественная корреляция.

Задачи статистики по изучению связей:

1. выявить наличие связей между явлениями

2. определить направление связей

3. оценить тесноту связей

4. определить форму связей, т.е. выразить связь аналитически.

10. Статистическая информация, ее значение и задачи в экономико-статистическом исследовании коммерческой деятельности.

Статистическая информация – это совокупность статистических данных, отображающих социально-экономические процессы и используемых в управлении экономикой и общественной жизнью.

Основным методом сбора информации о явлениях общественной жизни является статистическое наблюдение. Сбор статистической информации, то есть статистическое наблюдение, является начальной стадией статистического исследования. Ошибки, допущенные на этом этапе, влияют на правильность и достоверность теоретических и практичских выводов.

Статистическое наблюдение - это планомерный, научно-организованный и, как правило, систематический сбор данных о явлениях общественной жизни. Оно осуществляется путем регистрации заранее намеченных существенных признаков с целью получения в дальнейшем обобщающих характеристик этих явлений.

Отчетность является основным источником статистической информации и предусматривает систему регламентированных показателей, характеризующих деятельность предприятий. Она имеет свои преимущества, так как формируется на основе первичного учета, обеспечивающего сопоставление и контроль данных.

Различают несколько видов отчетности. Прежде всего, выделяют типовую и специализированную отчетность. Типовая имеет единую форму и содержание для всех предприятий и отраслей народного хозяйства. Специализированная присуща тем предприятиям или производствам, которые имеют специфические особенности.

По периодичности представления различают еженедельную, двухнедельную, месячную, квартальную, годовую.

По способу представления – срочная (телеграфная) и почтовая.

По порядку прохождения отчетность разделяют на централизованную и децентрализованную. Централизованная проходит через систему государственной статистики. Децентрализованная обрабатывается в соответствующих министерствах и ведомствах и сводки представляют статистическим органам.

Статистическая информация - показатели, рассчитанные по совокупности компаний, фирм, корпораций, банков и других организаций, рынкам , географическим и административным территориям и т.д.

Статистическая информация - это цифровая информация в виде числовых рядов различных показателей, прогнозных моделей и оценок. Данные представлены в виде средних или относительных величин и позволяют выявлять закономерности развития социально-экономических явлений и процессов.

Статистическая информация предоставляется чаще всего государственными службами, а также компаниями, занятыми исследованиями и разработками, консалтинговыми фирмами.

Одним из важнейших источников информации являются статистические публикации отдельных стран и специализированных органов ООН по экономике и отдельным отраслям.

В России основным источником статистической информации яляется Государственный комитет по статистике и ряд коммерческих и полукоммерческих структур созданных на его базе.

Базы данных статистической информации подразделяются на:

• базы данных глобальной статистики

• базы данных национальной статистики

БД содержат показатели по развитию всего хозяйство в целом, макроэкономические показатели как в мировом масштабе, так и по отдельным регионам или странам, по национальному доходу и валовому продукту с разбивкой по отраслям, данные по занятости населения, денежному обращению, ценах, охватывая статистику производства, финансов, торговли, потребления.

Госкомстат осуществляет подготовку, издание и распространение экономико-статистических и информационных материалов, в частности, тематических и отраслевых статистических сборников, бюллетеней и т.д.

Адекватность рассматривается как способность отразить именно те свойства явлений, которые подлежат исследованию. Это достигается логическим и статистическим обоснованием показателя на стадии его проектирования. Точность измерения зависит от структуры показателя, организации наблюдений и обработки данных.

Одним из непременных условий правильного восприятия и тем более практического использования статистической информации, квалифицированных выводов и обоснованных прогнозов является знание статистической методологии изучения количественной стороны социально-экономических явлений, природы массовых статистических совокупностей, значения и познавательных  свойств показателей статистики, условий их применения в экономическом исследовании.

        В настоящеее время перед статистической наукой встают  актуальные проблемы дальнейшего совершенствования системы показателей, приемов и методов сбора, обработки, хранения и анализа статистической информации. Это имеет важное значение для развития и повышения эффективности автоматизированных систем управления, создания  автоматизированных банков данных, распределительных банков данных и т.д., которые в свою очередь могли бы способствовать созданию автоматизированной системы коммерческой информации