1.5.2. Иррациональные уравнения

1-й способ

Замена иррационального уравнения смешанной системой

Пример 1. Решить уравнение

Решение

Область допустимых значений неизвестного:

Введем новые неизвестные, положим:

Получим смешанную систему:

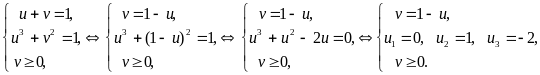
Все значения входят в область допустимых значений и являются решениями уравнения.

Ответ:

Пример 2. Решить уравнение

Решение

Найдем область допустимых значений неизвестного

Положим тогда

умножим обе части первого уравнения на -3 и сложим со вторым уравнением, получим

При такой подстановке заданное уравнение примет вид

Получим систему уравнений

не является корнем, так как значит

Ответ:

Пример 3. Решить уравнение:

Решение

Положим отсюда получаем уравнение:

Каждый из модулей последнего уравнения обращается в нуль при соответственно, значит полученное уравнение рассмотрим на следующих трех промежутках (см. рис. 6):

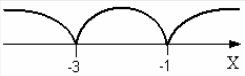
Рис. 6

1. При уравнение примет вид:

- входит в промежуток .

2. При получим уравнение:

- уравнение не имеет корней.

3. При получим уравнение:

- входит в промежуток

Таким образом, в результате решения получены два корня и

Но один из них не входит в область допустимых значений и является посторонним корнем. Остается один корень

Тогда получим

Проверка

Ответ:

Пример 4. Решить уравнение:

Решение

Положим тогда Получим систему уравнений, из которой исключим x:

Заменяя в данном уравнении и получим уравнение

Объединим два полученных уравнения в систему и решим ее:

Решим полученное уравнение

Отсюда получаем:

Ответ:

2-й способ

Возведение обеих частей уравнения в одну и ту же степень

При решении иррациональных уравнений этим способом надо иметь в виду следующие теоремы о равносильности уравнений.

Теорема 1. Уравнение равносильно на множестве действительных чисел уравнению

Теорема 2. Уравнение равносильно на множестве действительных чисел смешанной системе

При решении уравнений этим способом множество допустимых значений неизвестных может расшириться. Это иногда приводит к появлению посторонних решений, которые не будут принадлежать множеству допустимых значений неизвестных.

Кроме того, если при возведении обеих частей уравнения в четную степень не накладывать условия (теорема 2), тогда могут появиться посторонние решения, принадлежащие области допустимых значений неизвестного данного уравнения. В этом случае необходимо делать проверку корней, принадлежащих области допустимых значений неизвестных подстановкой их в данное уравнение.

Пример 1. Решить уравнение:

Решение

Найдем область допустимых значений переменной

Возведем обе части уравнения в квадрат, получим

не входит в область допустимых значений .

Ответ:

Пример 2. Решить уравнение на множестве действительных чисел

Решение

1-й способ

Область допустимых значений неизвестного найдем из решения системы неравенств:

Преобразуем уравнение: Обе части полученного уравнения неотрицательны, возведем их в квадрат, получим:

Перед тем, как возводить обе части этого уравнения в квадрат, необходимо потребовать, чтобы правая часть была неотрицательна:

При этом область допустимых значений неизвестного сузиться, в самом деле (см. рис. 7):

Рис. 7

Область допустимых значений станет:

Возведем обе части уравнения в квадрат получим:

и является посторонним корнем.

Ответ:

2-й способ

Область допустимых значений

Оба корня входят в ОДЗ, т. е. и