Приклад виконання лабораторної роботи

Завдання про коробку максимального обсягу.

Математична постановка завдання. Є квадратна заготовка із гнучкого матеріалу, що має довжину сторони L (мал. 2). Із цієї заготовки варто вирізати чотири рівних квадрати зі стороною r по її кутах, а отриману фігуру зігнути, так щоб вийшла коробка без верхньої кришки. Завдання полягає в такому виборі розміру квадратів, що вирізуються, щоб у результаті вийшла коробка максимального обсягу.

Рисунок 2 - Схема виготовлення коробки із прямокутної заготівлі

Для математичної постановки даного завдання необхідно визначити змінні відповідні завдання оптимізації, задати цільову функцію й специфікувати обмеження. У якості змінної варто взяти довжину сторони квадрата, що вирізується, r, що у загальному випадку, виходячи з постановки завдання, приймає неперервні дійсні значення. Цільовою функцією є об’єм отриманої коробки. Оскільки довжина сторони підстави коробки дорівнює: L -2r, а висота коробки рівна r, то її об’єм знаходиться по формулі: V(r) = (L - 2r)²* r.

Виходячи з фізичних міркувань, значення змінної r не можуть бути від’ємними й перевищувати величину половини розміру вихідної заготівлі L, тобто 0,5 * L.

З метою уніфікації, позначимо змінну через х= r. Тоді математична постановка завдання про коробку максимального обсягу може бути записана в наступному виді:

f(x) = x*(L-2x)² max, де _={x R¹ |0≤x≤0,5*L]. (4)

Цільова функція даного завдання є нелінійною, тому завдання про коробку максимального розміру ставиться до класу завдань нелінійного програмування або нелінійної оптимізації.

Рішення завдання про коробку максимального об’єму за допомогою програми MS Excel

Не зменшуючи загальності математичної постановки завдання (4) припустимо: L=1. Для рішення даного завдання за допомогою програми Ехсel створимо нову книгу з ім'ям Нелінійна Оптимізація й змінимо ім'я її першого аркуша на Завдання про коробку. Зробимо необхідні написи в комірках А1:В2. Після цього введемо в комірку С2 формулу: =С1*(1-2*С1)^2, що представляє цільову функцію (4). Зовнішній вигляд робочого аркуша Excel з вихідними даними для рішення завдання про коробку максимального обсягу має такий вигляд (рис. 3).

Рисунок 3 – Вихідні дані для рішення завдання про коробку максимального обсягу

Для подальшого рішення завдання варто скористатися інструментом пошуку рішення програми MS Excel. Із цією метою необхідно виконати операцію головного меню: Сервіс | Пошук рішення.

Примітка

Варто врахувати, що при першому звертанні до інструмента пошуку рішення можна не виявити в головному меню Сервіс операції Пошук рішення. Це означає, що компонент пошуку рішення в програмі MS Excel не встановлений. Тому для продовження роботи необхідно попередньо встановити даний компонент, для чого варто виконати операцію головного меню: Сервіс | Надбудови й установити відмітку в рядку з ім'ям Пошук рішення.

Після виклику інструмента пошуку рішення з'явиться діалогове вікно майстра завдання параметрів для знаходження рішення (мал. 4).

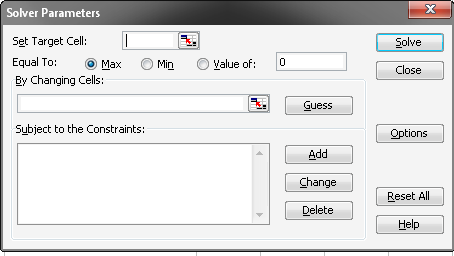
Рисунок 4 - Діалогове вікно Пошуку рішення

Перше діалогове вікно Пошук рішення має наступні елементи:

• поле Встановити цільову комірку — використовується для задання посилання на комірку, у якій задана формула з вираженням цільової функції розв'язуваного завдання оптимізації;

• перемикачі в групі Рівної — визначають характер розв'язуваного завдання оптимізації. Для знаходження рішення з максимальним значенням цільової функції цей перемикач ставиться в положення максимальному значенню, для знаходження рішення з мінімальним значенням — у положення мінімальному значенню. Нарешті, для знаходження рішення, при якому цільова функція приймає деяке фіксоване значення, перемикач ставиться в положення Значенню, праворуч від якого можна ввести необхідне фіксоване значення;

• поле Змінюючи комірки — служить для вказівки комірок, які повинні змінюватися в процесі пошуку рішення завдання. Саме в цих комірках повинні перебувати змінні розв'язуваного завдання оптимізації;

• у багатостроковому полі Обмеження відображаються обмеження розв'язуваного завдання оптимізації. Для завдання обмежень призначене додаткове вікно Додавання обмеження;

• кнопка Припустити — служить для автоматичного заповнення поля Змінюючи комірки, які зазначені у формулі завдання цільової функції;

• кнопка Додати — служить для виклику додаткового вікна Додавання обмеження (рис. 5);

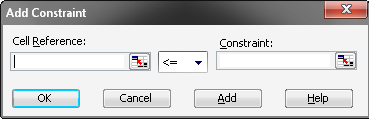
Рисунок 5 - Діалогове вікно Додавання обмеження

• кнопка Змінити — служить для виклику додаткового вікна Додавання обмеження, у якому буде відображене обмеження, обране в багатостроковому полі Обмеження;

• кнопка Видалити — служить для видалення обмеження, обраного в багатостроковому полі Обмеження;

• кнопка Виконати — служить для запуску процесу знаходження оптимального рішення після специфікації всіх параметрів пошуку рішення;

• кнопка Закрити — служить для закриття діалогового вікна Пошук рішення;

• кнопка Параметри — служить для виклику додаткового вікна Параметри пошуку рішення (мал.6) для специфікації додаткових параметрів пошуку рішення, частина яких уже задана за замовчуванням;

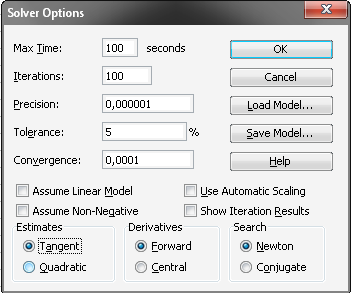
Рисунок 6 - Діалогове вікно Параметри пошуку рішення

• кнопка Відновити - служить для очищення полів даного діалогової вікна й відновлення значень параметрів пошуку рішення, використовуваних за замовчуванням;

• кнопка Довідка - служить для одержання довідкової інформації про елементи діалогового вікна Пошук рішення.

Діалогове вікно Додавання обмеження (мал.4) призначене для завдання одного обмеження й має наступні елементи:

• поле Посилання на комірку - служить для вказівки комірки або діапазону комірок, у яких утримується ліва частина обмеження, що задається;

• список, що випадає, у центрі вікна - містить перелік знаків нерівностей обмежень, а також можливість специфікації вимоги цілочисельності або двійкових значень змінних. Майстер пошуку рішень припускає специфікацію обмежень у вигляді рівностей і нерівностей;

• поле Обмеження - служить для вказівки комірки, діапазону комірок або конкретного числа, яке специфікує праву частину обмеження, що задається;

Діалогове вікно Параметри пошуку рішення (мал.5) призначене для специфікації додаткових параметрів знаходження рішення або зміни вже заданих параметрів. Варто відмітити, що значення більшості цих параметрів, використовуваних за замовчуванням, підходять для рішення типових завдань оптимізації. Діалогове вікно Параметри пошуку рішення має наступні елементи:

• Поле Максимальний час служить для обмеження часу, що відпускається на пошук рішення завдання. У це поле можна ввести час (у секундах), що не перевищує 32 767. Установлене за замовчуванням значення 100 підходить для рішення розглянутих типових завдань.

• Поле Граничне число ітерацій служить для обмеження часу рішення завдання за допомогою задачі деякого граничного числа проміжних обчислень. Установлене за замовчуванням значення 100 підходить для рішення розглянутих типових завдань.

• Поля Відносна похибка і Припустиме відхилення служать для задачі точності, з якою буде виконуватися пошук рішення. В окремих випадках доцільно після знаходження рішення зі значеннями цих параметрів, заданими за замовчуванням, повторити обчислення з більшою точністю й меншим припустимим відхиленням. Після виконання пошуку рішення зрівняти отримані результати.

• Прапорець Лінійна модель служить для прискорення пошуку рішення завдання оптимізації з лінійною цільовою функцією й лінійними обмеженнями. Для завдань нелінійної оптимізації цей прапорець повинен бути скинутий, а для завдань лінійного програмування - установлений, оскільки в противному випадку можливе одержання невірного результату.

• Прапорець Показувати результати ітерацій служить для припинення пошуку рішення для перегляду результатів окремих ітерацій.

• Прапорець Автоматичне масштабування служить для включення автоматичної нормалізації вхідних і вихідних значень, якісно відмінних по величині, - наприклад, максимізація прибутку у відсотках стосовно вкладень, обчислених у мільйонах рублів.

• Прапорець Невід’ємні значення дозволяє встановити нульову нижню границю для тих комірок, для яких вона не була зазначена в поле Обмеження діалогового вікна Додати обмеження.

• Параметри групи Оцінки служать для вказівки методу екстраполяції (лінійна або квадратична) використаного для одержання вихідних оцінок значень змінних у кожному одномірному пошуку.

При цьому:

- перемикач лінійна служить для використання лінійної екстраполяції вздовж дотичного вектора, що дає кращі результати при рішенні лінійних завдань;

- перемикач квадратична служить для використання квадратичної екстраполяції, що дає кращі результати при рішенні нелінійних завдань.

• Параметри групи Різниці служать для вказівки методу чисельного диференціювання (прямі або центральні похідні), що використовується для обчислення часток похідних цільових і обмежуючих функцій. При цьому:

- перемикач прямі використовується в більшості завдань, де швидкість зміни обмежень відносно невисока;

- перемикач центральні використовується для функцій, що мають розривну похідну. Даний спосіб вимагає більше обчислень, однак його застосування може бути виправданим, якщо видається повідомлення про те, що одержати більше точне рішення не вдається.

• Параметри групи Метод пошуку служать для вибору алгоритму оптимізації (метод Ньютона або сполучених градієнтів) для вказівки напрямок пошуку. При цьому:

- перемикач Ньютона забезпечує вибір для знаходження рішення квазіньютонівського методу, що вимагає більше пам'яті, але виконується за менше число ітерацій, чим у методі сполучених градієнтів;

-перемикач сполучених градієнтів забезпечує вибір для знаходження рішення методу сполучених градієнтів, що вимагає менше пам'яті, але виконується за більше число ітерацій, чим у методі Ньютона. Даний метод варто використати, якщо завдання досить велике, і необхідно заощаджувати пам'ять, а також, якщо ітерації дають занадто малу відмінність у послідовних наближеннях.

Продовжується рішення завдання про коробку максимального об’єму . У першому вікні майстра пошуку рішення треба в поле з ім'ям Установити цільову комірку - указати комірку $C$2, у якій утримується формула для розрахунку цільової функції завдання, а в поле з ім'ям Змінюючи комірки ввести абсолютну адресу комірки $С$1, у яку буде записане шукане рішення завдання.

Після цього варто додати два обмеження на припустимі значення змінної. Для цього варто нажати кнопку Додати, у результаті чого з'явиться додаткове вікно завдання обмежень (мал. 7). Для уведення адрес комірок у ліву частину обмеження призначене поле з ім'ям Посилання на комірку.

Форма нерівності обмеження вибирається з вкладеного списку в середній частині вікна. Нарешті, для задання правої частини обмежень у поле введення з ім'ям Обмеження варто ввести із клавіатури наступні числа: 0,5 — для першого обмеження та 0 — для другого.

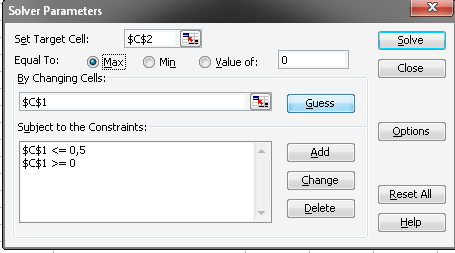
Рисунок 7 - Параметри майстра пошуку рішення для завдання про коробку

Інші параметри майстра пошуку рішення, для редагування яких призначене додаткове друге вікно цього майстра, можна залишити без зміни. Остаточний зовнішній вигляд діалогового вікна майстри пошуку рішення після завдання необхідної інформації зображений на мал. 7.

Після завдання необхідних параметрів пошуку рішення можна приступити до виконання чисельних розрахунків, для чого варто нажати кнопку Виконати. Після виконання чисельних розрахунків програмою MS Excel практично миттєво буде отримане кількісне рішення, що має такий вигляд (мал. 8).

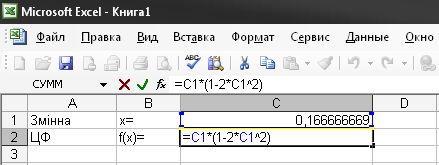
Рисунок 8 - Результат кількісного рішення завдання про коробку максимального обсягу

Інтерпретуючи отримані кількісні значення, можна прийти до наступного висновку. Результатом рішення є оптимальне значення сторони квадрата, що вирізується: ropt=0, 166 693 69 при якому виготовлена коробка буде мати максимальний обсяг V max = 0, 074 074 074 073. Нагадаємо, що це рішення відповідає довжині сторони вихідної заготівлі, рівної 1.

Для аналізу знайденого рішення можна побудувати графік цільової функції (4) і візуально оцінити його коректність. Із цією метою на окремому робочому аркуші за допомогою операції автозаповнення комірок задається послідовний ряд чисел вихідної змінної г у діапазоні від 0 до 1 з інтервалом 0,01, які запишемо в комірки з адресами А2:А52. Поруч в комірки В2:В52 записуються відповідні значення цільової функції (4). Для цього можна записати формулу: =А2* (1-2*а2) ^{^}2 в комірку В2 і за допомогою операції автозаповнення "протягти" зміст цієї комірки на діапазон В3:В52.

Побудований графік цільової функції буде мати такий вигляд (рис. 9).

Візуальний аналіз цього графіка показує, що максимум цільової функції перебуває між значеннями х = 0,16 і х = 0,17. Цей факт можна також перевірити, порівнявши значення в комірках В18 і В19. Тим самим, можна зробити висновок про коректність отриманого результату рішення даного завдання оптимізації.

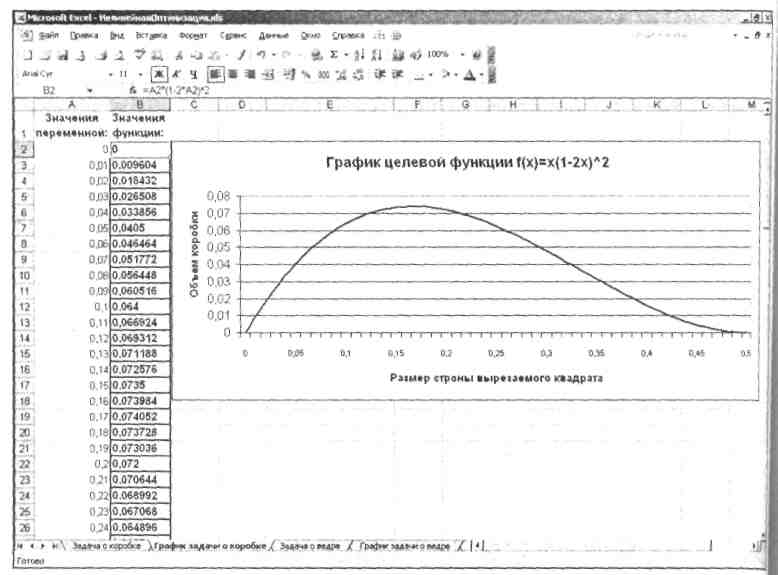
Рисунок 9 - Графік цільової функції в завданні про коробку максимального об’єму