10. Последовательность независимых испытаний, или испытания Бернулли.

Пусть производится серия из n испытаний, в каждом из которых событие А наступает с вероятностью P(A)=p>0. Событие А, за появлением которого мы наблюдаем, принято называть успехом, а противоположное ему событие - неудачей.

Def Последовательность испытаний называется последовательностью независимых испытаний, или испытаниями Бернулли, если вероятность успеха в каждом испытании есть величина постоянная Р(А)=р>0 и не зависит

1. от номера испытания;

2. от результатов предыдущих испытаний.

ПРИМЕРЫ:

1. Производится n выстрелов по мишени (без пристрелки!). Успехом является событие А - поражение мишени.

2. Подбрасываем монету n раз. Успех - выпадение герба.

3. В семье 5 детей. Успехом будем считать рождение мальчика.

Найдем вероятность того, что в семье ровно 3 мальчика. Считается, что вероятность рождения мальчика равна 51%, а вероятность рождения девочки - 49%. Обозначим успех в данной серии из 5 испытаний (рождение мальчика) буквой М, а неудачу (рождение девочки) - буквой Д.

Введем событие В - из 5-ти детей ровно 3 мальчика, а также вспомогательные события, выражающие последовательность появления детей:

В₁=МММДД - три старших сына, и так далее аналогично

В₂=ММДМД, В₃=ММДДМ,..., В_m=ДДМММ.

Ясно, что, во-первых, В=В₁+В₂+...+В_m , во-вторых, события В_i, B_j несовместны при i¹j, и, в-третьих, т.к. рождение мальчиков или девочек - независимые в совокупности события, P(B₁)=P(МММДД)=P(М)P(М)P(М)P(Д)P(Д)=(0,51)³(0,49)².

Аналогично вычисляются вероятности остальных событий В_i, причем все эти вероятности равны, так как отличаются лишь порядком сомножителей. Осталось выяснить, сколько таких событий, или чему равно число m. Ответ очевиден - столько, сколько существует различных 5-тибуквенных слов, в которых 3 буквы М и 2 буквы Д. Вспомнив еще раз пример с абракадаброй из параграфа 1, получим . Применяя формулу вероятности суммы несовместных событий, найдем

.

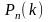_Т_ Пусть - вероятность успеха в серии из испытаний Бернулли, - вероятность неудачи, - вероятность того, что в серии из независимых испытаний успехов ровно . Тогда справедлива формула:

.

Доказательство проведите самостоятельно, используя предыдущий пример.

ПРИМЕР: (О вероятности хотя бы одного события в схеме Бернулли)

В семье 5 детей. Какова вероятность того, что хоть один из них мальчик?

Пусть событие F - в семье есть хотя бы один мальчик. Вероятность этого события можно искать двумя способами.

Способ 1: , где событие - в семье ровно мальчиков. Ясно, что события попарно несовместны, так что можно применить формулу вероятности суммы несовместных событий. Получим:

,

где =0,51 - вероятность рождения мальчика, =0,49 - вероятность рождения девочки. Осталось подставить значения и получить ответ.

Способ 2: Задачу можно решить быстрее и с меньшим риском ошибиться в подсчетах, если воспользоваться противоположным событием - в семье мальчиков нет совсем.

.