7. Формула полной вероятности.

ПРИМЕР:

Рассмотрим пример на интуицию.

№ 1 № 2

Пусть имеются две коробки, а также 10 купюр по DM 10 и столько же купюр по DM 20. Некто подходит к любой из коробок и вытягивает одну купюру. Как следует разложить купюры, чтобы с наибольшей вероятностью попалась бы купюра в DM 20?

Возможные варианты ответа (собранные за многолетнюю практику работы со студентами) запишем в виде таблицы:

коробка № 1

коробка № 2

5	5	5	5
0	10	10	0
10	10	0	0
0	1	10	9

Как нам подсказывает интуиция, последний способ, по-видимому, является самым подходящим. Вернемся к теории (вероятностей).

_Т_ Пусть событие A, события такие, что

1. A ,

2. ,

3. при любых ,

4. ;

Тогда полная вероятность события вычисляется по формуле:

.

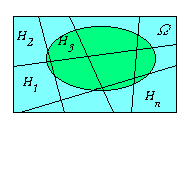
Def Система множеств {H_i}, удовлетворяющая условиям 1) - 4), называется полной группой событий, каждое из событий H_i называется гипотезой.

NOTE: Вместо условия 4) достаточно потребовать, чтобы .

Доказательство: Разобьем пространство элементарных исходов  на множества так, как указано в условии теоремы.

, .	Событие можно представить в виде: ,причем события и несовместны, если . Тогда, пользуясь аксиомой конечной аддитивности и формулой вероятности произведения событий, окончательно получим: Q.E.D.

ПРИМЕР: Вернемся к примеру с коробками и деньгами. Найдем вероятность того, что будет вытащена крупная купюра в каждом из четырех случаев раскладки денег по коробкам.

В качестве гипотез естественно выбрать следующие:

- выбираем купюру из коробки №1;

- выбираем купюру из коробки №2.

Так как коробки две, и, по условиям эксперимента, выбираем одну или другую из них с равной вероятностью, ясно, что . Найдем требуемые условные вероятности и полную вероятность события в каждом из перечисленных в таблице случае.

Случай 1: ,

Случай 2: ,

Случай 3: ,

Случай 4: ,

8. Апостериорная оценка вероятности гипотезы. Формула Байеса.

Пусть нам известен результат эксперимента, а мы хотим узнать, какая из гипотез осуществилась с большей (или меньшей) вероятностью. Такие оценки, проводимые после опыта, называют апостериорными в отличие от оценок, проводимых до опыта и называемых априорными.

_Т_ (Формула Байеса)

Известно, что произошло событие А. Вероятность того, что при этом осуществилась гипотеза , равна

.

Здесь - полная группа событий, а вычисляется по формуле полной вероятности.

Доказательство: Воспользуемся два раза формулой вероятности произведения: .

Q.E.D.

ПРИМЕР:

Пусть в приведенном в предыдущем параграфе примере деньги разложены следующим образом:

коробка № 1

коробка № 2

5	3	5	7

Известно, что произошло событие А - вытащили купюру в DM 20. Требуется найти вероятность того, что доставали эту купюру из первой коробки.

Рассмотрим те же самые гипотезы и - купюра извлекается из коробки №1 или №2 соответственно. Априорные вероятности осуществления этих гипотез мы уже знаем - . Надо найти апостериорную оценку . Воспользуемся формулой Байеса: , где , , .

.

Как и следовало ожидать, апостериорная оценка вероятности первой гипотезы меньше 1/2, потому как в первой коробке меньше крупных купюр, чем во второй коробке.

Найдите самостоятельно вероятность того, что купюра DM 20 была вытащена из коробки №2, и убедитесь, что .