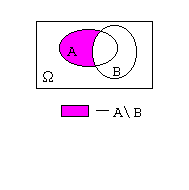2. Вероятностное пространство (ap).

1. Пространство элементарных событий.

Def Пространство элементарных событий  множество объектов произвольной природы.

Обычно в эксперименте множество множество взаимоисключающих исходов.

ПРИМЕРЫ :

1.

	Монета подбрасывается один раз. Элементарными исходами эксперимента являются 2 события: выпадение герба и выпадение решетки. (При описании элементарных исходов мы сразу оговариваем, что монета не может встать на ребро, зависнуть в воздухе или внезапно исчезнуть.) Таким образом, если обозначить элементарные исходы эксперимента Г - выпадение герба, Рвыпадение решетки, то пространство элементарных исходов является множеством, состоящим из двух элементов .
2.		Игральную кость подбрасывают один раз. Наблюдаемое событие - число выпавших очков. Элементарные исходы: выпало 1 очко, выпало 2 очка и т.д. - выпало 6 очков. .
3.			Монета подбрасывается до первого появления герба. Элементарными исходами эксперимента являются события: Г - герб появился при первом подбрасывании=РГ - герб появился при втором подбрасыванииk=РРР...РГ - герб появился при k-м подбрасывании получим: В этом случае пространство элементарных исходов - бесконечное счетное множество.

4.

Производится стрельба по плоской круглой мишени. Элементарные исходы - координаты точки попадания. В этом случае пространство элементарных исходов - несчетное множество.

2. Алгебра событий a.

Def Случайным событием называется любое подмножество пространства элементарных событий .

Обычно события обозначаются большими печатными латинскими буквами (кроме буквы P).

ПРИМЕР

Рассмотрим пример с подбрасыванием игральной кости. Как было показано ранее, пространство элементарных исходов

Событиями в данном эксперименте могут быть, например,

А - выпало четное число очков,

В - выпало число очков, кратное трем.

, .

Используем этот пример при рассмотрении того, какие возможны

Операции над событиями

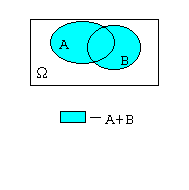
Суммой событий А и В называется множество, обозначаемое А+В=А В и состоящее из элементов, входящих в А или В. В приведенном выше примере А+В= , это означает, что выпало либо четное число очков, либо число очков кратно трем.

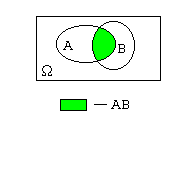
Произведением событий А и В называется множество, обозначаемое АВ=А В и состоящее из элементов, входящих в А и В. В приведенном выше примере АВ= , это означает, что выпало четное число кратное трем.

Разностью событий А и В называется множество, обозначаемое А\В и содержащее те элементы множества А, которые не входят в В. В приведенном выше примере А\В= , что означает - выпало четное число очков не кратное трем.

Def Событие называется достоверным.

Def Событие называется невозможным.

Def Событие называется противоположным событию .

Def События А и В называются несовместными, если АВ=Æ.

Def Если AÌB, то говорят, что событие A влечет событие В..

ПРИМЕРЫ

1. Событие А – “горит красный свет светофора” и событие В – “горит зеленый свет”, несовместны.

2. Событие А – “на игральной кости выпало два очка” влечет событие В – “выпало четное число очков”.

Свойства событий:

1. AA=A

2. A+A=A

3. A+

4. A =A

5. A

6. AB=BA

7. A+B=B+A

8. A(B+C)=AB+AC

9. (AB)C=A(BC)

10. (A+B)+C=A+(B+C)

11. 

12. 

Эти свойства докажите самостоятельно.

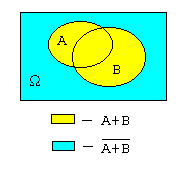
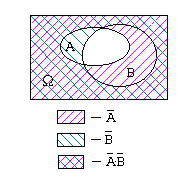
Формулы де Моргана.

13. 

1. 

Докажем, например, предпоследнее свойство с помощью картинки, к которой часто прибегают в теории множеств.

Из картинок видно, что множества и состоят из одних и тех же элементов. (Можно провести и строгое доказательство, но мы не будем этого делать, т.к. оно абсолютно не наглядно.)

NOTE: Понятия произведения и суммы событий переносятся на бесконечную последовательность событий.

Def Пусть пространство элементарных событий. A - некоторый класс подмножеств множества . A - алгебра событий, если "A,BÎA

1. A

2. ABÎA

3. A+BÎA

4. A – BÎA

NOTE: Из свойств 1 и 4 следует, что A.

ПРИМЕРЫ

1. A =

2. A = , где - некоторое событие.

3. Система всех подмножеств множества  также является алгеброй событий.

ПРИМЕР Вспомним эксперимент с подбрасыванием игральной кости. Пусть алгебра событий A - система всех подмножеств множества .

A =

Сколько элементов в множестве A?

Таким образом, если множество конечно, то и алгебра A конечна.