18. Статический расчет системы. Определение координат центра тяжести объекта.

Исходным при проектировании системы амортизации являются не только параметры внешних механических воздействий, но и законченная компоновка устройства, т.е. считаются известными габариты устройства (блока), место установки, габариты, масса различных частей блока (узлы, детали), кроме этого существуют ограничения на типоразмер амортизатора. Необходимым является наличие всех характеристик для применяемого типа амортизатора.

На первом этапе в блоке аппаратуры выделяются элементарные узлы простейшей геометрической формы. При этом из сборочного чертежа всегда можно определить координаты центра тяжести этого элементарного блока относительно любой выбранной первоначальной системы координат. Для элементарного блока координаты его центра тяжести должны быть достаточно просто определяемыми. Рекомендуется первоначально выбирать систему так, чтобы одна ось проходила через ребро куба.

2. Определение реакций амортизаторов.

Различают две схемы нагружения амортизаторов: а) однонаправленная схема; б) пространственная схема нагружения.

а) Однонаправленная схема нагружения должна отвечать следующим условиям:

• реакция виброизоляторов и нагрузка на них образуют систему параллельных сил;

• блок в положении равновесия должен устанавливаться без перекосов;

г де G - суммарный вес блока, P_i -реакции амортизаторов.

Эта система возможна при установке блоков без перекосов.

В однонаправленной схеме нагружения неизвестной является реакция амортизатора и число неизвестных зависит от количества амортизаторов. Реакции виброизоляторов определяются на основе уравнений статистики. Для однонаправленной схемы:

My = 0; Mx = 0; n – число амортизаторов;

При n = 3, ищем P₁, P₂, P₃, (система из 3-х уравнений). При n = 3 система статически определима, и мы из исходной системы непосредственно находим три неизвестных реакции. При n = 4 система статически неопределима и необходимо четвертое уравнение. Его получают за счет введения дополнительного условия на расположение амортизаторов.

Дополнительные условия задаются за счет соответствующего выбора координат установки амортизаторов. Для такой системы P₁ = P₂ = P₃ = P₄ = G/4 . Здесь дополнительное условие – симметрия виброизоляторов – вылилось в подобное решение системы.

1.

Всегда при и реакция P₁ = P₂ = … = P_n = G/n

2. Здесь дополнительное условие таково:

P1+P2 = P3+P4; (P1+P4)b’ = (P2+P3)b; P2 = P3; P1 = P4.

Для того, чтобы система была статически определима необходимо задать n - 3 дополнительных условия!

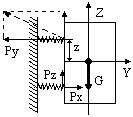
б) Пространственная схема нагружения.

Это не однонаправленная схема (произвольное нагружение). Здесь кроме вертикальных нагрузок возникают составляющие по другим направлениям. Реакция – векторная сумма реакций по трем составляющим: Pi = {Pzi; Pxi; Pyi}.

Таким образом для пространственной схемы нагружения неизвестными являются не реакции, а составляющие реакций. При n амортизаторах имеем 3n неизвестных.

И з 6-ти уравнений определяем 6 неизвестных. Т.о. число дополнительных условий, которое необходимо задать 3n –6. Дополнительные условия получаем аналогично как и для схемы а).

Итак, считаем, что нам известны либо реакции (для схемы а), либо составляющие реакций (схема б). На этом расчет закончен.

32. Методики расчёта на ударные воздействия (упрощённая и метод эквивалентных прямоугольных импульсов).

1. Упрощённая методика.

   Здесь удар трактуется мгновенным. При этом принимают потенциальную энергию, определяемую деформацией равной нулю. . Следовательно, вся кинетическая энергия, за­пасённая за время удара, полностью переходит в потенциальную энергию максимально сжатых амортизаторов.

m – известна;

При заданной форме ударного импульса параметры системы и определяются следую­щим образом (при ):

Для типовых форм ударных импульсов формул для расчета и приводятся в соответствующих таблицах.

Методика определения ускорения объекта сводится к следующим действиям:

1. По ударной характеристике энергоёмкости системы (определяем максимальную деформацию амортизаторов:

2. По максимальной деформации, с помощью силовой ударной характеристики, определяем максимальную ударную силу: .

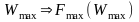3. По максимальной ударной силе определяем ускорение объекта по формуле:

Этот алгоритм действителен и для метода эквивалентных прямоугольных импульсов.

О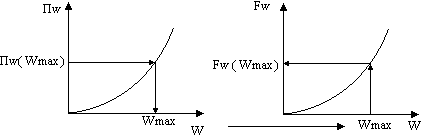 ценим погрешность этого расчёта:

знаменатель известен, числитель определяется то графику энергоемкости, т.к. значение известно.

ТЕПЛО- И МАССОБМЕН В ЭВС. ЗАЩИТА ЭВС ОТ ТЕПЛОВЫХ ВОЗДЕЙСТВИЙ.