9.11. Энергетические соотношения в системе виброизоляцииции.

Допустим, существует система c S степенями свободы.

1. Кинематическая энергия системы «Т».

q1 q2 – для S=2 q1 q2, q1 q3, q2 q3 – для S=3 S – число степеней свободы.

a_ij - инерционный (кинетический) параметр системы

	При поступательном движении объекта.
	При поворотных движениях объекта.

- обобщенные скорости по соответствующим координатам (скорости абсолютные).

2. Потенциальная энергия объекта «П».

Сij – жесткостной параметр системы:

q_i, q_j – деформации упругих элементов (относительные).

3. Диссипативная функция «Ф».

b_ij – коэффициент демпфирования.

3. Уравнение Лагранжа (уравнение движения объекта).

I II III

L=T-П - функция Лагранжа.

i – число обобщенных координат, равное числу степеней свободы.

I - баланс кинетической и потенциальной энергии в системе.

II - потери энергии на диссипацию.

III - приток энергии за счет возмущающих сил.

В частных случаях Q(t) равно нулю:

1. при свободном движении объекта (смещение блока от положения равновесия)

2. кинематическое возмущение

Данное уравнение позволяет проанализировать движение системы с любой степенью свободы и в любой момент времени. Для системы c S степенями свободы уравнение Лагранжа превращается в систему из S дифференциальных уравнений. При S=6 уравнение Лагранжа – система из 6-ти уравнений.

Решение в общем виде подобной системы – сложная задача даже при использовании ЭВМ.

При S = 1 - система решается.

При S > 1 – применяются упрощенные методы расчета системы.

10. характеристики виброизоляторов, используемых при расчёте системы на ударные воздействия и их применение

Расчёт системы амортизации при ударном воздействии.

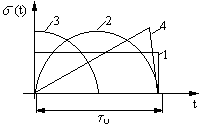
Воздействующий ударный импульс задаётся функцией ударного ускорения от времени. Импульс имеет произвольную форму, но при расчётах и испытаниях приняты следующие типовые формы импульсов:

Прямоугольная форма. Косинусоидальная форма (пол-волны). Косинусоидальная форма (четверть волны). Треугольник любой формы.

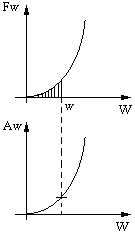
ьХарактер движения объекта при ударе определяется воздействующим ударным импульсом, массой объекта и ударными характеристиками виброизоляторов . Ударные характеристики виброизоляторов :

	Силовая ударная характеристика Fw(W) - зависи­мость ударной силы от деформации.
	Ударная энергоёмкость Пw(W) - определяет потен­циальную энергию виброизолятора в зависимости от де­формации.

Связь между характеристиками такова: .

Для нормализованных виброизоляторов приводятся обе указанные харак­теристики, снятые экспериментально, причем для различных направлений виброизоляторов характеристики также будут различны.

Д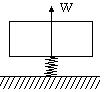 алее предположим, что удар направлен вдоль оси W.

Для расчёта системы строят суммарные ударные характеристики. Сумми­рование ударных характеристик производится по координатам. Далее в расчетах используются эти суммарные характеристики.