Лекция 7 ряды динамики (продолжение), индексы (начало)

Прирост и темп прироста. Обратимся снова к нашему примеру с анализом выплавки стали. Исчислим в табл. 10.8 показатели при­роста выплавки стали и темпы прироста.

Таблица 10.8

Приросты и темпы прироста выплавки стали в СССР за 1970—1973 гг.

Показатели	1970 г.	1971 г.	1972 г.	1973 г.	1974 г.	1975 г.
Выплавка стали (у — уровни ряда динамики), млн. т Прирост (у), млн. т:	115,9	120,9	125,6	131,5	136,2	141,3
по годам	-	48 '1	4,9	5,9	4,7.	51 0,1 ".у
к 1970 г.	-	4,8	9,7	15,6	20,3	25,4
Темп прироста, %:
по годам *	-	4,14	4,06	4.70	3,57	3,74
К 1970 г.		-4,14	8,37	13,46	17,52	21,92
Абсолютное значение одного про­цента прироста, млн. т	-	1,159	1,207	1 1,256	1,315	1,362

Абсолютный прирост (_у) исчисляют как разность уровней ряда и выражают в единицах из­мерения показателей ряда. Абсо­лютные приросты можно исчислить за отдельные периоды .ряда (_у = у_i - у_{i - 1}) и как накопленные итоги с начала ис­следуемого периода (у_б = у_i - у_{i - 1}) В первом случае из каждого уровня вычитают предыдущий (цепной способ расчета), а во втором из всех уровней ряда вычитают начальный.

По цепным значениям абсолютных приростов (у_ц) вычис­ляется показатель среднего годо­вого абсолютного прироста (у-). Для его расчета используют схему средней арифметической про­стой:

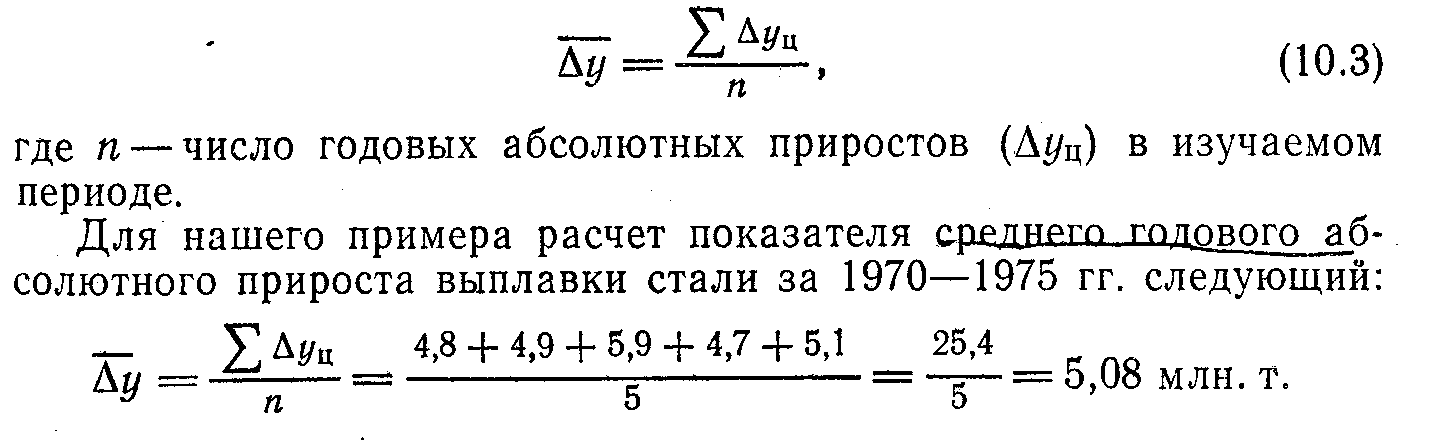
Для определения среднего абсолютного прироста можно вос­пользоваться на­копленным абсо­лютным приростом (у_б). В этом случае применяют следующую формулу:

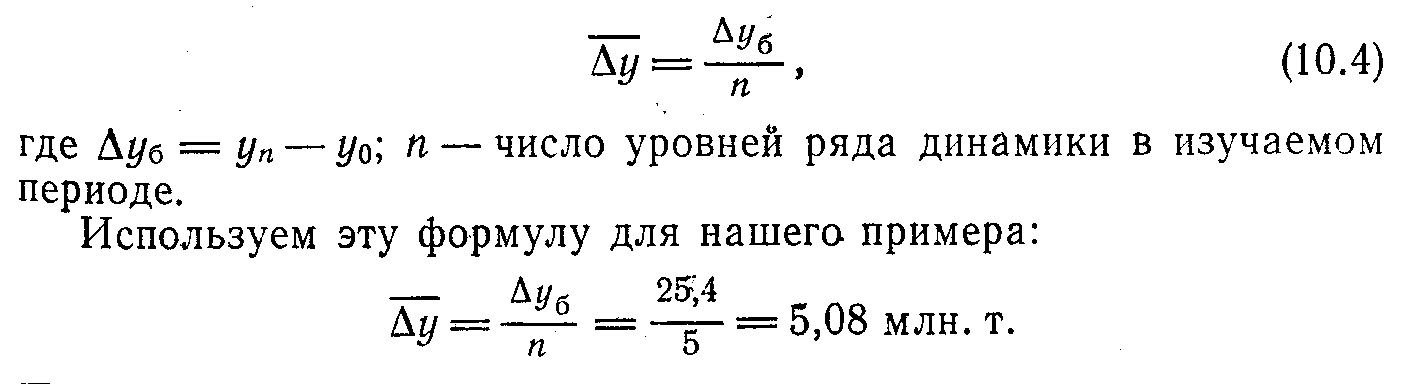
Показатель абсолютного значения 1% прироста () равен частному от деления абсолютного прироста на темп прироста ( = у_ц / Ту). А так как темп прироста равен частному от деления абсолютного прироста, умноженного на 100, на вели­чину первона­чального уровня, то абсолютное значение 1 % прироста оказы­вается равным первоначальному уровню, деленному на 100 ( = 0,01 * у_{i - 1}).

Исчисление средних темпов роста и прироста. При анализе раз­вития явле­ния часто возни­кает потребность дать обобщенную характеристику интенсивности развития за длительный пе­риод. Для этого исчисляют средние (обычно среднего­довые) темпы (Т-). Выше были приведены темпы динамики выплавки чугуна за 1970— 1975 гг. Погодовые (цепные) темпы составили:

1970 г. 1,041

1972 г. 1,041

1973 г. 1,047

1974 г. 1,038

1975 г. 1,037

Если величина признака образуется как произведение отдель­ных вариант, то правильной средней будет средняя геометриче­ская.

Значит, при расчете средних темпов динамики нужно применять среднюю геометрическую, т. е. перемножить цепные темпы роста и из произведения из­влечь корень, степень которого равна числу темпов.

Формула примет такой вид:

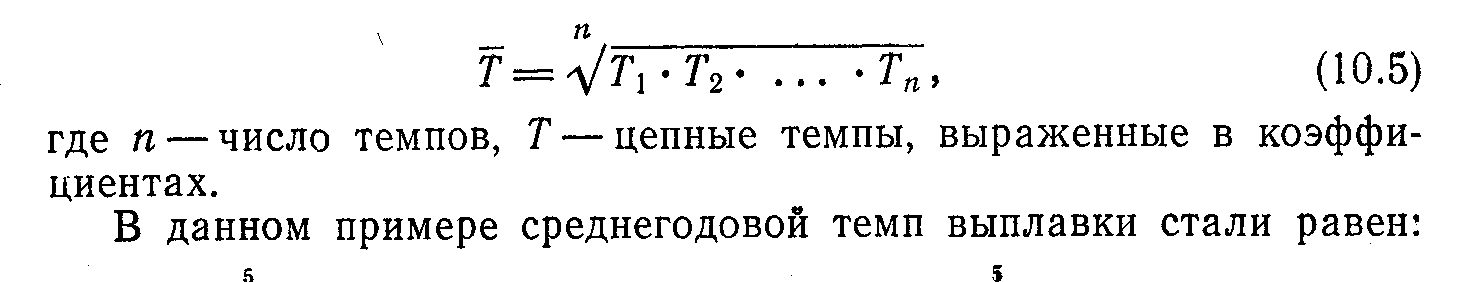
Т- =

Расчет производят с помощью логарифмов.

Следовательно, среднегодовой темп роста составил 1,040, или 104,0 %. Сред­негодовой темп прироста Т- был равен 4 %.

Например, если за 5 лет себестоимость продукции в какой-либо отрасли про­мышленности снизилась на 23 %, то расчет сред­негодового темпа снижения таков:

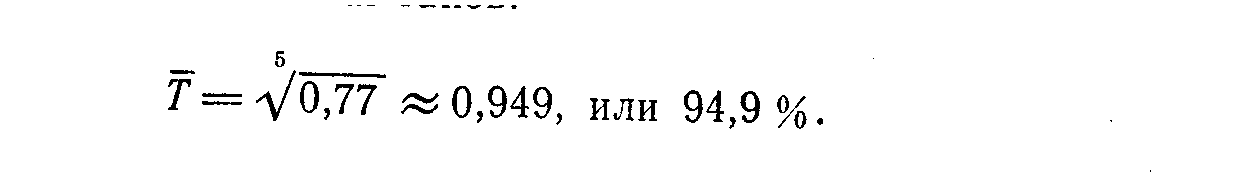
Это значит, что себестоимость продукции за 5 лет ежегодно сни­жалась в сред­нем на 5,1 % (100—94,9).

В экономическом анализе приходится иногда определять сред­ний темп роста по данным резко колеблющихся уровней динами­ческих рядов. В качестве примера воспользуемся данными об уро­жайности зерновых культур (ц с 1 га) по СССР в целом:

За 1966-1970 гг.
1965 г.	1966 г.	1967 г.	1968 г.	1969 г.	1970 г.
9,5	13,7	12,1	14,0	13,2	15,6
	За 1971 -1975 гг.
1970 г.	1971 г.	1972 г.	1973 г.	1974 г.	1975 г.
15,6	15,4	14,0	17,6	15,4	10,9

Если для расчета среднего темпа роста урожайности за 1971— 1975 гг. (девя­тая пятилетка) взять за базу 1970 г. и исчислить среднегодовой темп по формуле (10.6), то расчет покажет сниже­ние урожайности в девятой пятилетке:

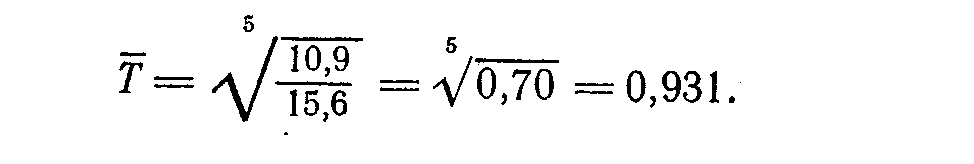
Урожайность снизилась за 5 лет на 30 % (10,9: 15,6), и средне­годовой темп снижения составил 6,9 %. Но это неправильно харак­теризует динамику урожайно­сти в девятой пятилетке. В самом деле, исчислим среднюю годовую урожайность за пять лет восьмой пятилетки. Она равна 13.72 ц с га ((13,7 + 12,1 + 14,0 + 15,6) / 5) = 68,6 / 5 = 13,72. Исчислим теперь среднюю годовую урожай­ность за пять лет девятой пятилетки. Она составит 14,66 ц. с га. ((15,4 + 14,0 + 17,6 + 15,4 + 10,9) / 73,3 = 14,661). Налицо рост сред­ней годовой урожайности в девятой пятилетке. Темп роста сред­него годового уровня составил 106,9% (14,66:13,72 == 1,069).